Минимизация функций
1.5.1 Задача минимизации
Пусть требуется построить логическую схему, которая реализует следующую таблицу истинности (рис. 1.20):
| №\X | a | b | c | f |
Рисунок 1.20 – Таблица истинности для логической схемы
Для реализации схемы запишем СДНФ:
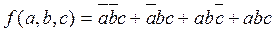
Каждый минтерм реализован своим конъюнктором. Инверсии выполнены на входах, чтобы не пользоваться дополнительными инверторами и не загромождать схему. Получаем (рис. 1.21):
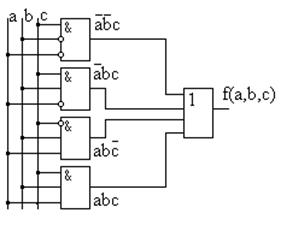
Рисунок 1.21 – Схемная реализация таблицы истинности (рис.1.20)
Сложность логической схемы принято оценивать общим числом входов всех ее элементов, которые условно называют ценой схемы. Инверторы не учитываются.
Найдём: чему равна цена нашей схемы:
Ц1=12 + 4 =16
Она складывается из числа входов конъюнкторов (элементы первого уровня) и числа входов дизъюнктора (элемент второго уровня).
Число входов элементов 1-го уровня равно числу символов в записи функции. Число входов элементов 2-го уровня равно числу термов в записи функции. То есть цену схемной реализации можно подсчитать сразу по исходной логической формуле.
Используя законы алгебры логики, попытаемся упростить исходную функцию.
Для этого вынесем за скобки: 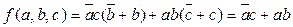
Очевидно, что реализация такой формулы значительно проще, ее цена Ц2=4+2=6.
Логическая формула с наименьшим числом логических связей называется минимальной.
Таким образом, получаем минимальную дизъюнктивную нормальную форму (МДНФ) и, соответственно, - МКНФ.
Процесс отыскания минимальной формы называется минимизацией логической функцииили просто минимизацией.
Минимизировать функции можно тремя методами:
1) расчетным путем, используя законы алгебры логики,
2) графическим путем (метод карт Карно или диаграмм Вейча), используя специальные карты,
3) расчетно-графическим путем (метод Квайна и его модификации).
Расчетный метод мы уже разобрали выше. Метод Квайна используется при числе переменных больше шести, хорошо алгоритмизируется и программируется. На его основе разработаны системы автоматизированного проектирования и различные стандартные программы минимизации логических функций любого числа переменных. Но они не всегда доступны и не оправданы при малом числе независимых переменных. Метод карт Карно хорошо работает при числе переменных меньше шести, прост и удобен для оперативного использования. Тем более, что большинство устройств, с которыми имеет дело разработчик, оперируют именно с малым числом переменных (3…5). Поэтому, рассмотрим этот метод подробнее.
1.5.2 Метод карт Карно
Карта Карно (минимизирующая карта) – это развертка некоторой объемной фигуры на плоскости. Карта Карно состоит из клеток, число которых равно числу наборов переменных функции. Каждая клетка соответствует строго определённому набору.
Например, карта Карно одной переменной (рис 1.22):
n = 1, число наборов N = 2n = 2

Рисунок 1.22 – Карта Карно одной переменной
Карта Карно двух переменных (рис.1.23):
n = 2, число наборов N = 22 = 4
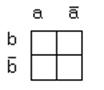 или так
или так 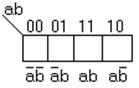
Рисунок 1.23 – Карта Карно двух переменных
Крайние клетки, соответствующие комбинациям 00 и 10 , являются соседними и отличаются одной переменной a.
Переменные в карте могут располагаться произвольно, но любые соседние по вертикали или по горизонтали клетки, могут отличаться не более чем одной переменной.
Карта Карно трёх переменных (рис.1.24):
n = 3, число наборов N = 23 = 8
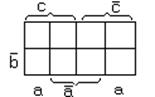 или так
или так 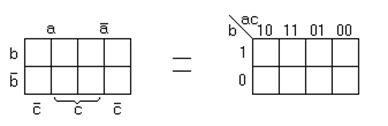
Рисунок 1.24 – Карта Карно трёх переменных
Если имеется функция трёх переменных, заданная следующей таблицей истинности (рис. 1.25):
| №\X | A | B | C | F |
Рисунок 1.25 – Таблица истинности произвольной функции
Тогда, соответствующая ей карта Карно выглядит так (рис. 1.26):

Рисунок 1.26 – Карта Карно функции рис. 1.25
Обычно нули в карту не пишут, а заносят только единицы.
Карта Карно четырёх переменных (рис. 1.27): n = 4, N = 16
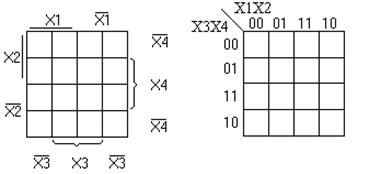
Рисунок 1.27 – Карта Карно функции четырёх переменных
В этих картах переменные расположены по-разному, но они обе правильны, так как любые соседние клетки по горизонтали или вертикали отличаются только одной из переменных. Клетки верхнего ряда соседние с клетками нижнего ряда, а клетки крайнего правого столбца соседние с клетками крайнего левого столбца.
Карта Карно пяти переменных (рис. 1.28): n = 5, N = 32. Это две шестнадцатиклеточных карты, отличающиеся только одной (пятой) переменной.
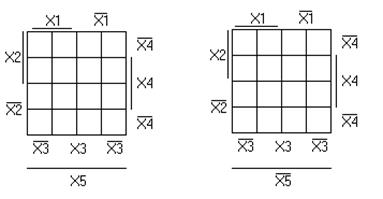
Рисунок 1.28 – Карта Карно функции пяти переменных
Карта Карно шести переменных (рис. 1.29): n = 6, N = 64. Это четыре шестнадцатиклеточных карты:
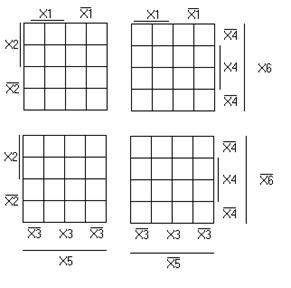
Рисунок 1.29 – Карта Карно функции шести переменных
Здесь любые клетки соседние, если они отличаются только одной переменной.
После заполнения карты единицами из таблицы истинности приступают к минимизации. Суть минимизации: охватить все единицы карты Карно наименьшим числом кубов наиболее высокого ранга. Из каждого куба выписывают минтерм общих переменных. Минтермы объединяют дизъюнктивно.
Куб– это прямоугольный или квадратный контур, содержащий клетки только с единицами:
одна единица – куб “0”-го ранга, так как 20 = 1
две единицы - куб “1”-го ранга, т.к. 21 = 2
четыре единицы - куб “2”-го ранга, т.к. 22 = 4
восемь единиц - куб “3”-го ранга, т.к. 23 = 8
шестнадцать единиц - куб “4”-го ранга, т.к. 24=16 и т.д.
Куб не может содержать другое число единиц и клетки с нулями. Одна и та же единица одновременно может принадлежать нескольким кубам, чтобы ранг куба был наибольшим. Тогда форма будет именно минимальной.
Пример 1.
Найти МДНФ такой функции: F(a,b,c)=V(1,3,6,7) . Составим её таблицу истинности, которая приведена на рис. 1.30
| №\X | a | b | c | f |
Рисунок 1.30 – Таблица истинности функции
Заполняем карту Карно:
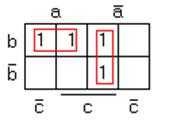
Рисунок 1.31 – Карта Карно функции рис. 1.30
Здесь следует провести два куба первого ранга и составить МДНФ:
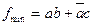
Запишем СДНФ исходной функции и преобразуем её по законам алгебры логики 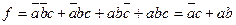 . Получили тот же результат.
. Получили тот же результат.
Представим карту Карно этой же функции по – другому (рис.1.32):

Рисунок 1.32 – Карта Карно функции рис. 1.30
Видно, что результат такой же 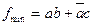 .
.
Пример 2.
Минимизировать функцию трёх переменных: F(a,b,c)= 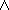 (0,4,5).
(0,4,5).
Начинаем с составления таблицы истинности (рис. 1.33)
| №\X | a | b | c | F |
Рисунок 1.33 – Таблица истинности
Карта Карно будет такой
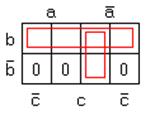
Рисунок 1.34 – Карта Карно функции (рис. 1.33)
и, соответствующая минимальная форма 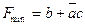 . Здесь первый куб содержит четыре единицы (ранг куба равен r = 2). Число переменных в минтерме равно
. Здесь первый куб содержит четыре единицы (ранг куба равен r = 2). Число переменных в минтерме равно
(n – r), где n = 3.
n – r = 3 – 2 = 1 – количество переменных из первого куба.
Из второго куба n – r = 3 – 1 = 2.
Составим СДНФ и выполним склеивание минтермов (конституент единицы) каждого с каждым:
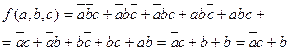
Первый склеиваем со вторым , затем с третьим, с четвёртым и т.д. Далее второй склеиваем с третьим, с четвёртым и т.д. Все минтермы пройдут через склеивание. После первого склеивания выполняется второе и т.д. пока оно возможно. Напомним, что минтермы для склеивания могут отличаться только одной переменной.
Пример 3.
Минимизировать функцию 2-х переменных:
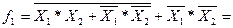 / приведем логическую формулу к нормальному виду
/ приведем логическую формулу к нормальному виду
( СДНФ )/ 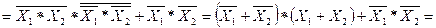
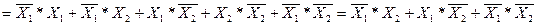
Составим карту Карно (рис. 1.35):
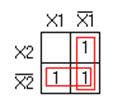
Рисунок 1.35 – Карта Карно функции
по которой получаем  . Этот же результат можно получить склеиванием минтермов.
. Этот же результат можно получить склеиванием минтермов.
Пример 4.
Минимизировать функцию четырёх переменных, карта Карно которой представлена на рис. 1.36.
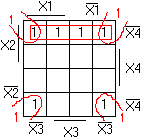
Рисунок 1.36 – Карта Карно исходной функции
Проводим два контура второго ранга и получаем
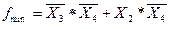
Цена схемы равна Ц = 4 + 2 = 6
Можно в карте Карно объединить нули, но при этом получаем инверсную функцию: 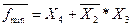 . Здесь проведены два куба – третьего и второго ранга. Цена схемы получается меньше. Ц = 2 + 2 = 4. Её реализация на произвольных элементах имеет вид (рис.1.37):
. Здесь проведены два куба – третьего и второго ранга. Цена схемы получается меньше. Ц = 2 + 2 = 4. Её реализация на произвольных элементах имеет вид (рис.1.37):
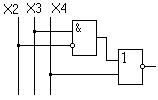
Рисунок 1.37 – Схемная реализация функции (рис. 1.36)
Отрицание можно перенести в правую часть, что не отражается на цене.
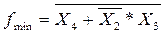
Чем меньше цена, тем лучше. Поэтому, минимизировать по карте Карно следует и по единицам и по нулям. К реализации принимают формулу с наименьшей ценой.
Пример 5.
Имеем функцию пяти переменных, заданную картой Карно (рис. 1.38).

Рисунок 1.38 – Карта Карно исходной функции
Здесь проводим три куба : 1 – куб второго ранга, 2 – куб третьего ранга, 3 – куб второго ранга. Записываем минимальную форму: 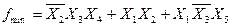 .
.
Находим цену Ц = 8 + 3 = 11. Желающие могут найти цену схемы после объединения нулей.
Дата добавления: 2016-01-18; просмотров: 3720;
