Виды областей значений функций принадлежности

На ряду с рассмотренным нами отображением m: х 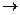[0,1] существуют и другие области значений, например m: х 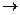[-1,1] или m: х 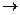[- 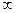, 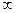], а также m: х 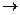L, где L – есть нечеткое множество, то есть функция принимающая значение в алгебраической структуре называемой решеткой.

Гетерогенные нечеткие множества

Если области значения нечетких множеств одинаковы или одна и та же, то они называются гомогенными. В противном случае, то есть когда функция принадлежности m L₁^(x1) L₂^(x2) ….. L_n^(xn) , то они являются гетерогенными (то есть нечеткие множества определены на различных областях).

Введение гетерогенных нечетких множеств и связанных с ними составных лингвистических переменных позволяют моделировать задачи многокритериального выбора, когда имеются признаки описываемые как в количественных, так и в порядковых шкалах.

Нечеткие операторы

(операторы агрегации нечеткой информации)

Рассмотренные нами бинарные операции (см. таблицу) соответствуют логическим связкам И и ИЛИ. Их исследованиям посвящен целый ряд работ в которых дается как экспериментальное, так и аксиоматическое обоснование этих операций. Было показано, что для любых нечетких множеств из класса F(x) операторы F=min, G=max являются единственно возможными операторами пересечения и объединения при выполнении следующих условий:

1. коммутативности

F(m_A, m_B)=F(m_B, m_A)

G(m_A, m_B)=G(m_B, m_A)

2. ассоциативности

F(m_A, F(m_B, m_C))=F(F(m_A, m_B), m_C)

G(m_A, G(m_B, m_C))=G(G(m_A, m_B), m_C)

3. монотонности

F(m_A, m_B)≤ F(m_C, m_D) если m_A≤ m_C

G(m_A, m_B)≤G(m_C, m_D) m_B≤ m_D

4 F(m_A, m_A)<F(m_B, m_B) если m_A< m_B

G(m_A, m_A)<G(m_B, m_B)

5. F(1, 1)=1

G(0, 0)=0

6. F(m_A, m_B)≤min(m_A, m_B)

G(m_A, m_B)≥max(m_A, m_B)

7. F,G – непрерывные функции

8. Дистрибутивность

F(m_A, G(m_B, m_C))=G(F(m_A, m_B), F(m_B, m_C))

Данная совокупность условий избыточна, вполне достаточно выполнение условий 2,3,4 6, 8. Более того если к условиям 3 и 8 добавить условие F(m_A, 1)=M(1, m_A)=m_A и G(0, m_A)=m_A, то эта совокупность условий будет достаточной для того, чтобы эти операторы были единственны для операций пересечение и объединение нечетких множеств.

Сложность практических задач требующих использование многозадачных лингвистических преобразований термов лингвистических переменных требует введение более сложных (обобщенных) нечетких операторов или параметризированных операторов дополнения, пересечения, объединения позволяющих учесть гибкость работы с операндами.

К числу таких обобщенных операторов относится определение операторов в классе t- норм – T и в классе t- конорм – Ť

Т:[0,1] [0,1] [0,1] 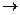удовлетворяющий условиям ограниченности, монотонности, комутативности и ассоциативности.

Ť:[0,1] [0,1] [0,1] 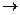удовлетворяющий условиям ограниченности (ограниченность Ť(1,1)=1 Ť(0, m_А)=Ť(m_А, 0)=m_А), монотонности, коммутативности и ассоциативности.

Указанные классы есть классы двойственных операторов. То есть Ť(m_А, m_В)=1-Т(1-m_А, 1-m_В)

Примеры обобщенных операторов:

t – нормы t – конормы

min (m_А, m_В) max (m_А, m_В)

Т_р(m_А, m_В)=m_Аm_В Ť_р(m_А, m_В)=m_А+m_В-m_Аm_В

Т_м (m_А, m_В)=max(0, m_А +m_В-1) Ť_м (m_А, m_В)=min( m_А +m_В)

—

Аналогично, на ряду, с оператором отрицания, имеющим вид m(х)=1-m(х) х Х существует набор и других операторов.

Наиболее общее определение функции отрицания в теории нечетких множеств следующее

с: [0,1] 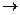[0,1] удовлетворяющее свойствам:

1. с(0)=1 с(1)=0

2. m_А≤m_В 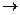с(m_А)≥с(m_В) – невозрастающая функция

Если ввести дополнительное условие, например что с – есть строго убывающая и непрерывная функция, то с – строгое отрицание.

Если ввести дополнительное условие, что с(с(m))=m, то будем иметь сильное отрицание или инволюцию.

Если с(с(m))≥m, то отрицание называется слабым.

Если с(с(m))≤m, то отрицание называется обычным.

Подобно тому, как существуют производящие функции, так и в теории нечетких множеств существуют генераторы операторов, и в частности генераторы отрицания

[Н1]