Показатели размытости
Можно выделить несколько аспектов связанных с понятием нечеткости или размытости:
1 аспект связан с интерпретацией показателя размытости, как меры отличия нечеткого множества от обычного или четкого множества (ближайшего к данному нечеткому множеству).
2 аспект связан с интерпретацией показателя размытости, как показателя внутренней неопределенности, двусмысленности, противоречивости обусловленных неполной, частичной принадлежностью объектов некоторому множеству.
3 аспект определен существованием нетривиального показателя размытости или показателя размытости специального вида, сущность которого вытекает из свойств алгебры нечетких множеств.
По 1 аспекту в качестве показателя размытости рассматривается два показателя: линейный индекс нечеткости и квадратичный индекс нечеткости. Первый определяется через расстояние Хемминга, а второй через Евклидово расстояние.
Они имеют следующий вид:
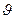 (A)=(2/n)d(A, Ä), Ä – обычное множество, ближайшее к данному.
(A)=(2/n)d(A, Ä), Ä – обычное множество, ближайшее к данному.
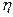 (A)=(2/
(A)=(2/ 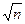 ) e(A, Ä), где d – обобщенное расстояние Хемминга
) e(A, Ä), где d – обобщенное расстояние Хемминга
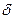 (A, B)=d(A, B)/n=(1/n)
(A, B)=d(A, B)/n=(1/n) 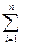 │mA(xi) - mA(xi)│ - относительное обобщенное расстояние Хемминга.
│mA(xi) - mA(xi)│ - относительное обобщенное расстояние Хемминга.
ε(A, B)=e(A, B)/ 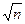 =
= 
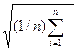 (m A(xi) - mA(xi))2 – относительное Евклидово расстояние.
(m A(xi) - mA(xi))2 – относительное Евклидово расстояние.
Пример: пусть А и В нечеткие множества
А={<0,7; x1>, <0,2; x2>, <0; x3>, <0,6; x4>, <0,5; x5>, <1; x6>, <0; x7>}
B={<0,2; x1>, <0; x2>, <0; x3>, <0,6; x4>, <0,8; x5>, <0,4; x6>, <1; x7>}
d(A, B)= │0,7-0,2│+│0,2-0│+│0-0│+│0,6-0,6│+│0,5-0,8│+│1-0,4│+│0-1│=2,6
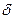 (A, B)=2,6/7=0,37
(A, B)=2,6/7=0,37
ε(A, B)= 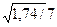 =0,5
=0,5
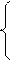 |
1, mA(x)>0,5
mÄ(x)= 0, mA(x)<0,5
0;1, mA(x)=0,5
Ä={<1; x1>, <0; x2>, <0; x3>, <1; x4>, <0; x5>, <1; x6>, <0; x7>}
d(A, Ä)/n=(│0,7-1│+│0,2-0│+│0-0│+│0,6-1│+│0,5-0│+│1-1│+│0-0│)/7=0,2
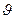 (A)=2
(A)=2 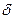 (A, Ä)=0,4
(A, Ä)=0,4
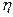 (A, Ä)=2 ε(A, Ä)=2 . 0,28=0,56
(A, Ä)=2 ε(A, Ä)=2 . 0,28=0,56
ε(A, Ä)= 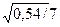 =0,28
=0,28
Пусть Е – универсальное множество, Е=[a, в]  R (непрерывное множество).
R (непрерывное множество).
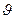 (A)=
(A)= 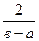
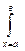 │mА(х)- mÄ(x)│dx
│mА(х)- mÄ(x)│dx
Справедливо следующее выражение для линейного индекса нечеткости.
 х
х  Ω : │mА(хi )- mÄ(xi) │=m A
Ω : │mА(хi )- mÄ(xi) │=m A 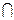 ┐A(xi)
┐A(xi)
┐A – дополнение к нечеткому множеству А,
отсюда
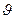 (A)=
(A)= 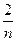
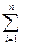 m A
m A 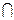 ┐A(xi)
┐A(xi)
а выражение 2 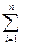 m A
m A 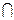 ┐A(xi) получило название индикатора нечеткости.
┐A(xi) получило название индикатора нечеткости.
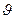 (A)=
(A)= 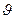 ( Ä)
( Ä)
Анализ проведенный для индексов нечеткости и операций 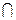 ,
, 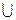 , ┐, показал, что ни одна из этих операций не дает систематического увеличения или уменьшения индекса нечеткости.
, ┐, показал, что ни одна из этих операций не дает систематического увеличения или уменьшения индекса нечеткости.
Введенный линейный индекс нечеткости можно записать так же следующим образом:
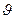 (A)=
(A)= 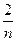
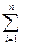 min {mА(хi ), m┐А(хi )}
min {mА(хi ), m┐А(хi )}
Перейдем к рассмотрению показателя размытости используемого с позиции 2 аспекта.
В качестве показателя размытости в этом случае используется понятие энтропии для нечетких множеств определяемое следующим образом:
H(πA(x1), πA(x2), …. πA(xn) )= 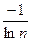
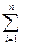 πA(xi)ln πA(xi)
πA(xi)ln πA(xi)
Здесь πA(xi)=mA(xi)/ 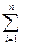 mA(xi)
mA(xi)
Пример: А – нечеткое множество с функцией принадлежности следующего вида:
mA(x1)=0,7
mA(x2)=0,9
mA(x3)=0
mA(x4)=0,6
mA(x5)=0,5
mA(x6)=1
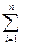 mA(xi)=3,7
mA(xi)=3,7
| i | 
| ||||||
| πA(xi) | 7/37 | 9/37 | 6/37 | 5/37 | 10/37 | ||
| Ln π | -1,67 | -1,4 | -1,8 | -2 | -1,3 | ||
| πA(xi) . Ln π | -0,32 | -0,34 | -0,29 | -0,27 | -0,35 | -1,57 |
Ln 6=1,79
1/ln 6=0,56
результат: H(πA(x1), πA(x2), πA(x3), πA(x4), πA(x5), πA(x6))=0,56 . 1,57=0,89
Сводка основных операций в алгебре нечетких множеств
| № | Название | Символическая запись F(x)/Ф([0,1]) | Логическая связка |
| Дополнение | —
m(х)= m(х)=1-m(х),  х х  Х
—
М(α)= М(α)=х\ Х
—
М(α)= М(α)=х\ 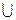 М/(1-β)
Β М/(1-β)
Β  [0,1], [0,1],  α α  [0,1] [0,1]
| не | |
| Пересечение 1 (минимум: невзаимодействующие переменные ) | m(х)= m1(х) 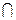 m2(х)
=min(m1(х), m2(х)), m2(х)
=min(m1(х), m2(х)),  х х  Х
M(α)= M1(α) Х
M(α)= M1(α) 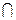 M2(α), M2(α),  α α  [0,1] [0,1]
| и и…и | |
| Объединение 1 (максимум: невзаимодействующие переменные ) | m(х)= m1(х) 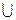 m2(х)
=max(m1(х), m2(х)), m2(х)
=max(m1(х), m2(х)),  х х  Х
M(α)= M1(α) Х
M(α)= M1(α) 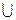 M2(α), M2(α),  α α  [0,1] [0,1]
| или либо…либо | |
| Пересечение 2 (ограниченное произведение) | m(х)= (m1 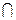 m2)х
=max[0, m1(х)+m2(х)-1] , m2)х
=max[0, m1(х)+m2(х)-1] ,  х х  Х
M(α)= Х
M(α)= 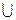 M1(β1) M1(β1) 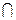 M2(β2), M2(β2),  α α  [0,1]
β1, β2>α [0,1]
β1, β2>α
| и | |
| Объединение 2 (ограниченная сумма) | m(х)= (m1 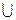 m2)х
=min[1, m1(х)+m2(х)] , m2)х
=min[1, m1(х)+m2(х)] ,  х х  Х
M(α)= Х
M(α)= 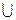 M1(β1) M1(β1) 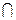 M2(β2), M2(β2),  α α  [0,1]
1≥β1, β2 ≥α [0,1]
1≥β1, β2 ≥α
| или | |
| Пересечение 3 (алгебраическое произведение) | m(х)= m1(х) . m2(х),  х х  Х
M(α)= Х
M(α)= 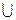 M1(β1) M1(β1) 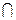 M2(β2), M2(β2),  α α  [0,1]
β1, β2>α [0,1]
β1, β2>α
| и | |
| Объединение 3 (алгебраическая сумма (*)) | m(х)= m1(х)*m2(х)= m1(х)+m2(х)-
m1(х) . m2(х),  х х  Х
M(α)= Х
M(α)= 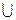 M1(β1) M1(β1) 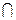 M2(β2), M2(β2),  α α  [0,1]
β1+β2 – β1 . β2≥ α, β1, β2 [0,1]
β1+β2 – β1 . β2≥ α, β1, β2  [0,1] [0,1]
| или | |
| Разность | m(х)= (m1(х)-m2(х)
=max[0, m1(х)-m2(х)] ,  х х  Х
M(α)= Х
M(α)= 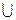 M1(β1) M1(β1)  M2(β2), M2(β2),  α α  [0,1]
β1-β2 ≤ α, β1, β2 [0,1]
β1-β2 ≤ α, β1, β2  [0,1] [0,1]
| ||
| Конденсация (возведение в степень) | mCOND(х)=m2(х) mS(х)=mа(х), а=0,5 dil | очень |
1 класс F(x)={m/ m: x 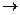 [0,1]}
[0,1]}
Ф([0,1])={М/ М:[0,1] 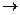 2x}
2x}
а) М(0)=0
б)  α1, α2
α1, α2  [0,1], α1 ≤α2
[0,1], α1 ≤α2 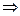 M(α1)
M(α1)  M(α2)
M(α2)
 | |||
 |



 α2
α2
α1
M(α2)
M(α1)
Связь между этими рассмотренными способами формализации нечеткости устанавливается теоремой представления. В соответствии с этой теоремой классы F и Ф изоморфны относительно операций объединений и пересечений. При этом любой бинарной операции в F(x) соответствует объединение пересечение различных срезов в Ф([0,1]).
 х
х  Х: m(х)= m1(х)*m2(х)
Х: m(х)= m1(х)*m2(х)  M(α)=
M(α)= 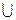 M1(β1)
M1(β1) 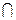 M2(β2),
M2(β2),  α
α  [0,1]
[0,1]
β1*β2≥α
Дата добавления: 2016-01-09; просмотров: 1321;
