Формы описания неопределенностей
Для учета и описания факторов неопределенности известны и используются следующие модели:
1. Стохастическая (вероятностная) модель
W(z) – плотность вероятности.
2. Статистическая модель (описывается статистической оценкой плотности вероятности или выборочными распределениями)
^
W(z) – оценка плотности вероятности.
3. Интервальная модель
(-z; z) – интервал.
4. Нечеткие модели в виде функции принадлежности μ(z) величины z нечеткому множеству А.[Н1]
Нечеткие множества
Определение 1: Обозначим через 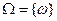 универсальное множество, тогда нечетким множеством Ã на множестве W называется совокупность пар следующего вида:
универсальное множество, тогда нечетким множеством Ã на множестве W называется совокупность пар следующего вида:
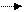 Ã={ω1, μà (ω)}, где μà (ω): Ω [0;1] и называется функцией принадлежности для нечеткого множества Ã.
Ã={ω1, μà (ω)}, где μà (ω): Ω [0;1] и называется функцией принадлежности для нечеткого множества Ã.
Если взять конкретный элемент 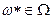 , то μÃ(
, то μÃ( 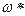 ) называется степенью принадлежности.
) называется степенью принадлежности.
Степень принадлежности есть субъективная мера того, что элемент 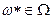 соответствует понятию, смысл которого формализуется нечетким множеством А.
соответствует понятию, смысл которого формализуется нечетким множеством А.
Определение 2: Носителем нечеткого множества А SА называется множество всех элементов принадлежащих универсалу и таких что степень принадлежности каждого больше 0
SА={ω/ω 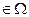 , μА(ω)>0}, SА подмножество универсального множества
, μА(ω)>0}, SА подмножество универсального множества 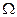
Определение 3: нечеткие множества А называются нормальными если выполняется следующее условие:
Sup μА(ω)=1
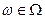
Для нечетких множеств - справедливы следующие операции:
 ПустьÃ, В – есть нечеткие множества на универсуме
ПустьÃ, В – есть нечеткие множества на универсуме 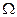
 Определение 4: Объединение нечетких множеств Ã, В называется множество
Определение 4: Объединение нечетких множеств Ã, В называется множество



 Ã
à 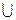 В = {ω, μà В(ω)}, μà В=max [μÃ(ω), μВ(ω)]
В = {ω, μà В(ω)}, μà В=max [μÃ(ω), μВ(ω)]
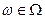
Определение 5: пересечением нечетких множеств Ã 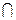 В называется нечеткое множество
В называется нечеткое множество



 Ã
à 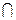 В = {ω, μà ∩В(ω)}, μÃ∩ В=min [μÃ(ω), μВ(ω)]
В = {ω, μà ∩В(ω)}, μÃ∩ В=min [μÃ(ω), μВ(ω)]
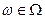
Определение 6: дополнение к нечеткому множеству Ã называется множество
 ┐à = {ω, μ┐à (ω)} для которого μ┐à (ω)= 1 – μÃ(ω)
┐à = {ω, μ┐à (ω)} для которого μ┐à (ω)= 1 – μÃ(ω)
Пусть Ãi есть нечеткое множество на 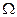 i тогда,
i тогда,
Определение 7: Декартовым произведением нечеткого множества А называется нечеткое множество Ã1  Ã2
Ã2  ……Ãn={<ω1, ….,ωn>, μÃ(ω1, ….,ωn)}, где ωi
……Ãn={<ω1, ….,ωn>, μÃ(ω1, ….,ωn)}, где ωi  Ωi
Ωi
μÃ(ω1, ….,ωn)= min { μÃ1(ω1), …., μÃn(ωn)}
Определение 8: Степенью 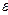 нечеткого множества Ã называется нечеткое множество
нечеткого множества Ã называется нечеткое множество
Аε={ω, μÃε(ω)} 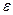 >0
>0
Частный случай: ε =2 то эта операция называется операцией сжатия или концентрации
ε =2 con (Ã)=Ã2
при ε =0,5 операция растяжения
dil (Ã)=Ã0,5
Отметим, что операция концентрации снижает степень нечеткости описания, а операция растяжения повышает.
Введем понятие множество α уровня.
Определение: множеством α уровня нечеткого множества à называется множество Sα={ω  Ω/μÃ(ω)≥α} при этом α=[0,1].
Ω/μÃ(ω)≥α} при этом α=[0,1].
Важность данного понятия состоит в том, что любое нечеткое множество может быть представлено объединением своих α уровневых четких множеств по всем α
mà (w)= 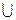 α mSα (w); где
α mSα (w); где
α  [0,1]
[0,1]
ó1, если mà (w) >=a
mSα (w)= í
è 0, если mà (w) < a
Пример: Пусть имеем два универсума
Ω1=(10,15,20,25)
Ω2=(5,6,7)
и нечеткие множества
Ã1={<10;1>,<15;0,8>,<20;0,5>,<25;0,3>}
Ã2={<5;1>,<6;0,5>,<7;0,2>}
Ã1  Ã2={<(10;5);1>,<(15;5);0,8>,<(20;5);0,5>,<(25;5);0,3>,<(10;6);0,5>,<(15;6);0,5>,
Ã2={<(10;5);1>,<(15;5);0,8>,<(20;5);0,5>,<(25;5);0,3>,<(10;6);0,5>,<(15;6);0,5>,
<(20;6);0,5>,<(25;6);0,3>,<(10;7);0,2>,<(15;7);0,2>,<(20;7);0,2>,<(25;7);0,2>}
Найдем CON (Ã1)=Ã12 и DIL (Ã1)=Ã10,5
Con (Ã1)={<10;1>,<15;0,64>,<20;0,25>,<25;0,09>}
Dil (Ã1)= {<10;1>,<15;0,89>,<20;0,71>,<25;0,55>}
α=0,3;0,5;0,8;1
| α | 0,3 | 0,5 | 0,8 | |
| Sα | 10;15;20;25 | 10;15;20 | 10;15 |
Ã=(10;15;20;25) 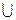 (10;15;20)
(10;15;20) 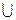 (10;15)
(10;15) 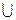 (10)
(10)
Определение 10: Имеем универсум Ω а также Ã1 и Ã2, степенью включения множества Ã1 в множество Ã2 называется величина
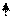
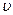 (Ã1, Ã2)= &[μÃ1(ω)
(Ã1, Ã2)= &[μÃ1(ω) 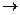 μÃ2(ω)]
μÃ2(ω)]
ω  Ω импликация
Ω импликация
2 способа нахождения импликации:
1. В логике Лукасевича
[μÃ1(ω) 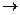 μÃ2(ω)]= 1&(1 - μÃ1(ω) + μÃ2(ω)]
μÃ2(ω)]= 1&(1 - μÃ1(ω) + μÃ2(ω)]
ω  Ω
Ω
2. По Заде
μÃ1(ω) 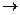 μÃ2(ω)= (1- μÃ1(ω))
μÃ2(ω)= (1- μÃ1(ω)) 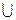 μÃ2(ω)
μÃ2(ω)
Определение 11: Степенью равенства нечетких множеств Ã1 и Ã2 называется величина следующего вида
η(Ã1;Ã2)= & (μÃ1(ω)∞μÃ2(ω)) 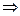 & [(μÃ1(ω)
& [(μÃ1(ω) 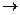 μÃ2(ω))&(μÃ2(ω)
μÃ2(ω))&(μÃ2(ω) 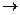 μÃ1(ω))]
μÃ1(ω))]
Пример: Ω={ω1;ω2;ω3;ω4;ω5}
Ã1={<ω2;0,1>;<ω3;0,6>;<ω5;0,4>}
Ã2={<ω1;0,8>;<ω2;0,5>;<ω3;0,7>;<ω5;0,6>}
В логике Лукасевича
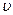 (Ã1, Ã2)= 1& [(0→0,8)&(0,1→0,5)&(0,6→0,7)&(0→0)&(0,4→0,6)]=
(Ã1, Ã2)= 1& [(0→0,8)&(0,1→0,5)&(0,6→0,7)&(0→0)&(0,4→0,6)]=
(1&(1-0+0,8)&(1-0,1+0,5)&(1-0,6+0,7)&(1-0+0)&(1-0,4+0,6))=
(1&1,8&1,4&1,1&1&1,2) 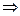 1
1
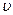 (Ã2, Ã1)=1& (0,8→0)&(0,5→0,1)&(0,7→0,6)&(0→0)&(0,6→0,4)=
(Ã2, Ã1)=1& (0,8→0)&(0,5→0,1)&(0,7→0,6)&(0→0)&(0,6→0,4)=
(1&(1-0,8+0)&(1-0,5+0,1)&(1-0,7+0,6)&(1-0+0)&(1-0,6+0,4))=
(1&0,2&0,8&0,9&1&0,8) 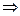 0,2
0,2
Дата добавления: 2016-01-09; просмотров: 1185;
