Основные теоретические положения. Основные теоретические положения
ЛИНЕЙНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Основные теоретические положения
Синусоидальным называется ток, изменяющийся во времени по синусоидальному закону. Значение тока в некоторый момент времени называется его мгновенным значением и обозначается малой буквой i. Ток считается определённым, если известен закон изменения его мгновенного значения и указано положительное направление. Для синусоидального тока
i(t) = Im×sin(wt + y ),
где: Im – максимальное значение или амплитуда тока;
= 2p/Т = 2pf – угловая частота;
T и f – период и частота тока;
y – начальная фаза.
Кроме амплитудного значения, он характеризуется еще и
средним Iср = 2Im /p, а также
действующим I = Im/ 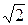 значениями.
значениями.
Пассивными элементами цепи синусоидального тока являются активное сопротивление R (учитывает преобразование электрической энергии в другие виды), индуктивность L (учитывает наличие магнитного поля и явление самоиндукции) и ёмкость C (учитывает наличие электрического поля). Состояние этих элементов при подключении их к напряжению u = Um×sinwt характеризуется данными табл. 3.1.
Таблица 3.1
| Элемент | Мгновенное значение тока | Закон Ома для действующих значений | 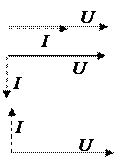 Векторная диаграмма Векторная диаграмма
|
| R | 
| 
| |
| L | 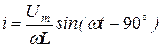
| 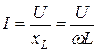
| |
| C | 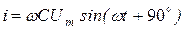
| 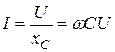
|
Основные величины, имеющие место в цепи с последовательным соединением R, L и C, если к ней подведено напряжение u = Um×sinωt, приведены в табл. 3.2.
При xL = xC, чего можно добиться, изменяя L, С или ω, в цепи R, L, С
возникает резонанс напряжений, и тогда UL = UС , UR = U, j = 0 (cosj =1), ток I = U/R имеет максимальное значение.
Таблица 3.2
| Цепь | Мгновенное значение тока | Закон Ома для действующих значений | Векторная диаграмма при xL>xC |
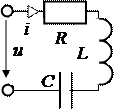
| i = 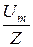 sin(ωt-j);
Z = sin(ωt-j);
Z = 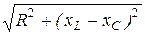 ;
j =arctg ;
j =arctg 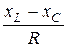
|
I = 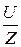
| 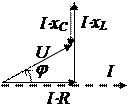
|
Если в цепи последовательно соединено по несколько R, L и С,то её полное сопротивление Z = 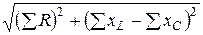 ,
,
а угол сдвига фаз напряжения и тока j = arctg 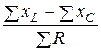 .
.
При параллельном соединении ветвей, в каждой из которых может быть включена любая комбинация R, L и С, токи раскладываются на активные (совпадающие с напряжением) и реактивные (перпендикулярные напряжению) составляющие. Для тока k-ой ветви Ikа= Ik×cosj k , Ikр = Ik×sinj k , Ik = 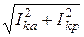 . Активная и реактивная составляющие тока в неразветвлённой части цепи, соответственно: Iа=SIkа , Iр=SIkр .
. Активная и реактивная составляющие тока в неразветвлённой части цепи, соответственно: Iа=SIkа , Iр=SIkр .
При расчёте параллельного соединения часто пользуются проводимос-тями ветвей. Активная, реактивная и полная проводимости k-ой ветви:
gk = 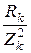 =
= 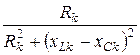 ; bk =
; bk = 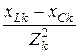 =
= 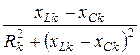 ; yk =
; yk = 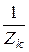 .
.
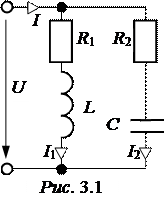 В схеме параллельного резонансного контура с потерями (рис. 3.1) при bL = bC или
В схеме параллельного резонансного контура с потерями (рис. 3.1) при bL = bC или 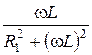 =
= 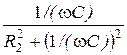 возникает резонанс токов. При этом I1р = I2р, j = 0 (cosj =1) и ток в нераз-ветвлённой части цепи имеет минимальное значение, если R1 и R2 меньше
возникает резонанс токов. При этом I1р = I2р, j = 0 (cosj =1) и ток в нераз-ветвлённой части цепи имеет минимальное значение, если R1 и R2 меньше 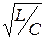 .
.
В схеме смешанного соединения, используя проводимости параллельно включенных ветвей, можно заменить их одной эквивалентной ветвью. После этого цепь будет представлять собой последовательное соединение, расчёт которого освещён выше.
При синусоидальном токе различают следующие мощности:
- мгновенную p(t) = u(t)×i(t),
- активную (среднее за период значение мгновенной мощности)
P = U×I×cosj = U×Iа = Uа×I = I 2×R = U 2×g,
- реактивную Q = U×I×sinj = ±U×Iр= ±Uр×I = ±I 2×x = ±U 2×b,
(здесь и далее в формулах верхний знак берётся в случае индуктивного характера нагрузки и нижний – в случае ёмкостного характера),
- полную S = U×I = I 2×Z = U 2×y.
В электроэнергетике большое значение имеет коэффициент мощности P/S = cosj. При его повышении возрастает эффективность использования оборудования и экономится электроэнергия. Для повышения используется обычно резонанс токов, а именно: параллельно нагрузке, которая носит, как правило, индуктивный характер, подключаются батареи статических конденсаторов.
Широкое распространение для расчёта цепей синусоидального тока получил комплексный (символический) метод, основанный на использовании теории комплексных чисел. Связь между синусоидальной величиной v(t)=Vm×sin(ωt+ψ) и комплексами: v=Im[Vm×ej(ωt+ψ)]=Im[Vm×ejωt×ejψ]=Im[Vm×ejωt], то есть (v¸V). Законы Ома и Кирхгофа в комплексной форме имеют точно та-кой же вид, как и при постоянном токе, нужно только использовать комплек-сы ЭДС, напряжений, токов и сопротивлений. В связи с этим цепи синусои-дального тока можно рассчитывать всеми методами, основанными на законах Ома и Кирхгофа и рассмотренными в разделе «Цепи постоянного тока».
Для любой ветви комплексное сопротивление
Z = R + j(xL – xC) = R ± jx = Z×e jj.
Используется и комплексная проводимость ветви Y= 1/Z= y×e-jj= g 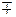 jb.
jb.
Комплексная мощность S = P + jQ = U× 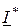 , то есть P = Re[U×
, то есть P = Re[U× 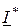 ], а Q = Im[U×
], а Q = Im[U× 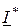 ]. В цепях синусоидального тока имеет место баланс не только активных мощностей, но ещё и реактивных.
]. В цепях синусоидального тока имеет место баланс не только активных мощностей, но ещё и реактивных.
Явление наведения ЭДС в одном контуре или катушке при изменении тока в другом контуре или катушке называется явлением взаимной индукции, а возникающая ЭДС еМ – ЭДС взаимоиндуции. В расчётах чаще используется напряжение, компенсирующее эту ЭДС: uМ = -еМ. Напряжение взаимной ин-дукции на k-ом элементе UМk = jwMkl×Il = jxMkl×Il = ZMkl×Il. При составлении уравнений по второму закону Кирхгофа знак напряжения определяется в со-ответствии со следующим правилом знаков: если направление обхода одной катушки и ток другой катушки относительно одноимённых зажимов совпада-ют, напряжение взаимоиндукции берётся с «плюсом», иначе – с «минусом».
При последовательном соединении двух индуктивно связанных элементов возможны их согласное и встречное включения. При согласном включении (в обоих элементах ток направлен одинаково относительно одноимённых зажимов) полное сопротивление цепи Zсогл = R + j(x + 2xМ), а при встречном – Zвстр = R + j(x – 2xМ).
Сложные цепи при наличии взаимной индуктивности рассчитываются путём решения уравнений, составленных по законам Кирхгофа, или методом контурных токов, причём явление взаимной индукции учитывается через напряжение UМk как указано выше. Применение метода эквивалентного гене-ратора возможно только в случае, если искомая ветвь не имеет индуктивной связи с ветвями двухполюсника. Остальные методы неприменимы.
При наличии общего узла у двух индуктивно связанных элементов часто применяется развязка индуктивной связи (замена исходной схемы эквивалентной, не содержащей индуктивной связи). Если к общему узлу элементы подключены одноимёнными зажимами, то к сопротивлениям элементов добавляется по –ZМ, а в общую ветвь включается +ZМ. Когда к общему узлу элементы подключены разноимёнными зажимами, знаки добавляемых сопротивлений меняются на противоположные.
Если токи в индуктивно связанных элементах I1 = I1×ejψ1 и I2 = I2×ejψ2 направлены относительно одноимённых зажимов одинаково, то передаваемая через взаимную индуктивность активная мощность
РМ1®2 = -РМ2®1 = Re[UМ1× 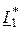 ] = Re[jωM×I2×
] = Re[jωM×I2× 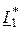 ] = wM×I1×I2×sin(y1 – y2).
] = wM×I1×I2×sin(y1 – y2).
Для измерения активной мощности всей цепи или её участка применяются ваттметры. Условное обозначение и схема включения ваттметра показаны на рис. 3.4, 3.5 (задачи 3.3, 3.4). По принципу действия ваттметра его показание определяется напряжением uW на катушке напряжения и током токовой катушки IW:
PW = uW×IW×cos 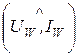 = Re[UW ×
= Re[UW × 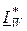 ].
].
Дата добавления: 2016-01-18; просмотров: 1074;
