РАСЧЁТ ПРОСТЕЙШИХ ЦЕПЕЙ
 3.2.1. Типовые примеры
3.2.1. Типовые примеры
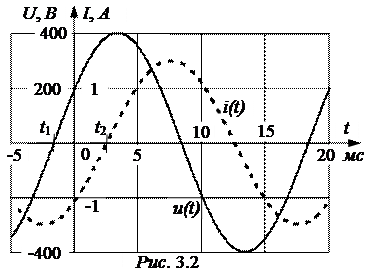
ЗАДАЧА 3.1. На рис. 3.2 приведены осциллограммы напряжения и тока. Требуется записать выражения для их мгновенных значений, определить действующие значения напряжения и тока.
Решение
По осциллограммам определяем период колебаний Т = 20 мс, следовательно, час-тота f =1/T = 50 Гц, а угловая частота w = 2pf = 314 рад/с. Начальные фазы напряжения и тока в градусах, соответственно:
ψu = -t1×(360/T) = 1,67×(360/20) = 30°, ψi = -t2×(360/T) = -2,5×(360/20) = -45°,
Амплитуды: Um = 400 B, Im = 1,5 A.
Следовательно, u(t) = 400×sin(314t+30°) B, i(t) = 1,5×sin(314t-45°) A.
Действующие значения: U = 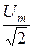 =
= 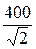 = 282 B, I =
= 282 B, I = 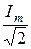 =
= 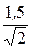 = 1,061 A.
= 1,061 A.
ЗАДАЧА 3.2. Цепь r, L с параметрами r = 35 Ом, L = 80 мГн питается от источника синусоидального напряжения частоты f = 50 Гц. Амплитудное значение напряжения питания Um= 200 B, а начальная фаза ψu = -20°. Рас-считать мгновенное и действующее значения тока. Построить векторную диаграмму цепи. Найти активную, реактивную и полную мощности цепи. Построить треугольник мощностей.
Решение
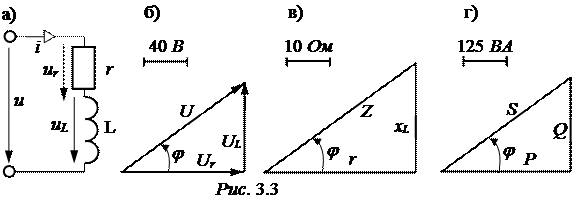
Приведём расчётную схему цепи (рис. 3.3,а).
 |
Запишем мгновенное значение приложенного к цепи r, L напряжения:
u(t) = Um×sin(ωt + ψu)= 200×sin(ωt – 20°) B.
Круговая частота ω = 2pf = 2p×50 = 314 рад/с.
Индуктивное сопротивление цепи xL= ωL = 314×80×10 -3 = 25,12 Ом.
По второму закону Кирхгофа для контура цепи u = ur + uL или в век-торной форме u = ur + uL. На основании этого уравнения строится вектор-ная диаграмма напряжений (рис. 3.3,б).
Треугольник сопротивлений цепи приведен на рис. 3.3,в. Это – прямо-угольный треугольник, из которого получаем
полное сопротивление цепи Z = 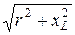 =
= 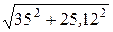 = 43,1 Ом
= 43,1 Ом
и угол сдвига фаз между током и напряжением
j = arctg 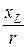 = arctg
= arctg 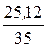 = 35,67°.
= 35,67°.
По закону Ома для амплитудных значений Im= 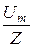 =
= 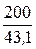 = 4,64 A.
= 4,64 A.
Начальная фаза синусоиды тока ψi = ψu – j = -20° – 35,67°= -55,67°.
Мгновенное значение искомого тока i(t) = 4,64×sin(314t – 55,67°) A.
Действующее значение тока I = 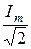 =
= 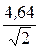 = 3,28 A.
= 3,28 A.
Действующие значения напряжений на участках:
- на резисторе ur = I× r = 3,28×35 = 115 B;
- на индуктивности uL = I× xL = 3,28×25,12 = 82,4 B;
- на входе цепи (напряжение сети) u = 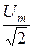 =
= 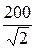 = 141,4 B.
= 141,4 B.
Активная мощность цепи P = U×I×cosj = I 2×r = 3,282×35 = 376,5 Bт.
Реактивная мощность Q= U×I×sinj = I 2×xL = 3,282×25,12 = 270,2 вар.
Полная мощность S = U×I = 141,4×3,28 = 464 BA.
Треугольник мощностей приведен на рис. 3.3,г.
Отметим, что на основании любого из треугольников рис. 3.3 можно рассчитать коэффициент мощности
cosj = 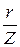 =
= 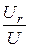 =
= 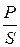 =
= 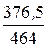 = 0,811 = cos35,67°,
= 0,811 = cos35,67°,
полученный ранее на основании треугольника сопротивлений цепи.
ЗАДАЧА 3.3. В цепи рис. 3.4,а протекает синусоидальный ток i(t) = 10×sin(ωt +15°) A частоты f = 400 Гц. Активные сопротивления r1 = = 10 Ом, r2 = 20 Ом, ёмкость С = 10 мкФ.
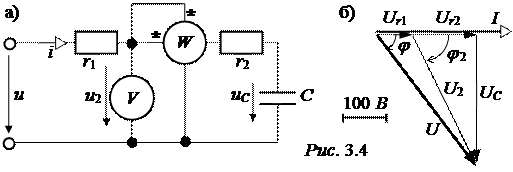 |
Рассчитать мгновенное значение напряжения сети u(t) и напряжения на конденсаторе uС(t). Найти показания вольтметра и ваттметра. Построить векторную диаграмму цепи.
Решение
Ёмкостное сопротивление xС = 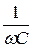 =
= 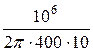 = 39,81 Ом.
= 39,81 Ом.
Дата добавления: 2016-01-18; просмотров: 1685;
