Задачи повышенной сложности. ЗАДАЧА 3.15. По показаниям приборов цепи рис
ЗАДАЧА 3.15. По показаниям приборов цепи рис. 3.13 определить параметры её элементов, если V ® 100 B; V1 ® 20 B; W ® 80 Bт; А ® 2 А.
 Ответы: r1 = 10 Ом, r2 = 20 Ом, х2 = 40 Ом.
Ответы: r1 = 10 Ом, r2 = 20 Ом, х2 = 40 Ом.
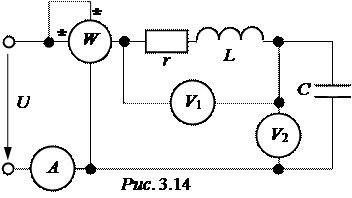
ЗАДАЧА 3.16. В схеме рис. 3.14 определить показание ваттметра, если u = 100 В, а показания приборов: А ® 1 А; V1 ® 150 B; V2 ® 100.
Ответ: Р = 198,4 Вт.
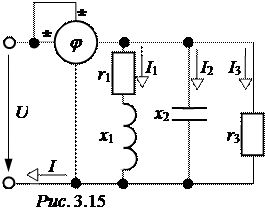
ЗАДАЧА 3.17. В схеме цепи рис. 3.15 задано: r1= r3; Р = 300 Вт; I1 = 5 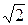 А; I2 = 5 А; фазометр показывает нуль. Опре-делить ток I, а также L и С. Частоту при-нять равной промышленной (f = 50 Гц).
А; I2 = 5 А; фазометр показывает нуль. Опре-делить ток I, а также L и С. Частоту при-нять равной промышленной (f = 50 Гц).
Ответы: I = 15 А, L = 6,37 мГн,
С = 796,3 мкФ.
 ЗАДАЧА 3.18. В схеме рис. 3.16 известно: u = 10 В; хL = 6 Ом; Р = 5 Вт.
ЗАДАЧА 3.18. В схеме рис. 3.16 известно: u = 10 В; хL = 6 Ом; Р = 5 Вт.
Определить сопротивление R.
Решение
Используем следующие соотношения:
Р = R×I 2 ; u = I× 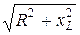 .
.
Тогда: I 2 = 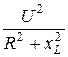 ; Р =
; Р = 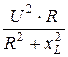 или Р×R 2 – u 2×R + Р×хL2 =0.
или Р×R 2 – u 2×R + Р×хL2 =0.
Отсюда R1,2 = 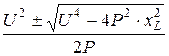 =
= 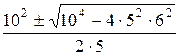 = 10 ± 8 Ом.
= 10 ± 8 Ом.
Задача имеет два ответа R1= 18 Ом и R2 =2 Ом.
 3.3. РАСЧЁТ СМЕШАННОГО СОЕДИНЕНИЯ С ИСПОЛЬЗОВА-НИЕМ МЕТОДА ПРОВОДИМОСТЕЙ
3.3. РАСЧЁТ СМЕШАННОГО СОЕДИНЕНИЯ С ИСПОЛЬЗОВА-НИЕМ МЕТОДА ПРОВОДИМОСТЕЙ
Типовые примеры
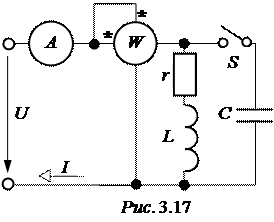
ЗАДАЧА 3.19. К цепи рис. 3.17 подведено напряжение u = 220 В. До подключения ёмкости С приборы показывали: А ® I=2 А; W ® P=40 Вт. Требуется определить минимально возможное показание амперметра после подключения ёмкости, а также величину последней.
Решение
До подключения ёмкости, используя показания приборов, определяем полное, активное и индуктивное сопротивления ветви с r, L:
Z = 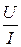 =
= 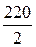 =110 Ом; r =
=110 Ом; r = 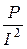 =
= 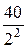 = 10 Ом;
= 10 Ом;
xL = 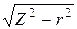 =
= 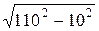 = 109,5 Ом.
= 109,5 Ом.
Минимальное значение тока в неразветвлённой части цепи будет иметь место при резонансе токов в цепи после подключения ёмкости, и в этом случае ток I будет иметь только активную составляющую: I = Ia = U×g, где g – активная проводимость всей цепи, равная активной проводимости ветви r, L, а именно: g = 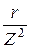 =
= 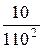 = 2,26×10 -4 См.
= 2,26×10 -4 См.
Тогда I = U×g = 220×2,26×10 -4 = 0,182 А.
Величину ёмкости определим из условия, что её реактивная проводимость должна равняться реактивной проводимости ветви r, L, т.е.
wС = 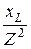 , откуда С =
, откуда С = 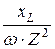 =
= 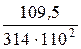 = 2,88×10 -5 Ф = 28,8 мкФ.
= 2,88×10 -5 Ф = 28,8 мкФ.
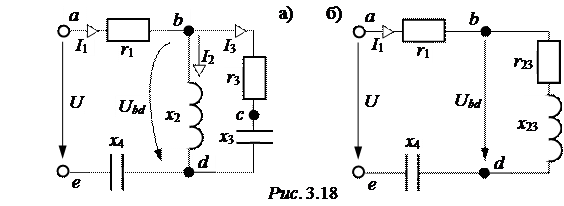 |
ЗАДАЧА 3.20. Для схемы (рис. 3.18,а) определить токи во всех ветвях и напряжения на всех участках, составить баланс активных и реактивных мощностей, построить полную векторную диаграмму цепи, записать мгновенные значения токов, если u(t) = Um×sin(wt +yu);
Um = 600 B; yu = -90°; r1 =10 Ом, r3 = x2 = x3 =20 Ом, x4 =20 Ом.
Решение
Заменим разветвлённый участок исходной схемы эквивалентной ветвью с параметрами r23, х23, для чего рассчитаем активные и реактивные (с учётом характера сопротивлений) проводимости параллельных ветвей:
g2 = 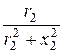 =
= 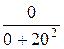 = 0; b2 =
= 0; b2 = 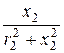 =
= 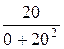 = 0,05 Cм (инд.);
= 0,05 Cм (инд.);
g3 = 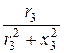 =
= 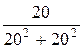 = 0,025 Cм; b3 =
= 0,025 Cм; b3 = 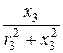 =
= 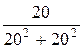 = 0,025 Cм (ёмк.);
= 0,025 Cм (ёмк.);
g23 = g2 + g3 = 0 + 0,025 = 0,025 Cм;
b23 = |b2 – b3| = 0,05 – 0,025 = 0,025 Cм (инд.);
r23 = 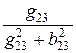 =
= 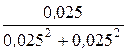 = 20 Ом;
= 20 Ом;
x23 = 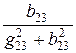 =
= 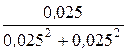 = 20 Ом (инд.).
= 20 Ом (инд.).
Эквивалентная схема, по которой рассчитаем ток в неразветвлённой части цепи, приведена на рис. 3.18,б: i1(t) = I1m×sin(wt +yu – j вх);
где I1m = 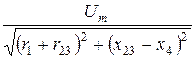 =
= 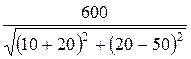 = 10
= 10 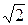 А;
А;
j вх = arctg 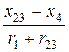 = arctg
= arctg 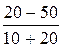 = -45°.
= -45°.
Дата добавления: 2016-01-18; просмотров: 2610;
