Следовательно, мгновенное значение тока
i1(t) = 10 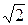 ×sin(wt – 90° + 45°) = 10
×sin(wt – 90° + 45°) = 10 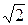 ×sin(wt – 45°) А,
×sin(wt – 45°) А,
действующее значение тока I1 = 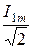 = 10 А.
= 10 А.
Напряжение на параллельно включенных ветвях
ubd(t) = Ubdm×sin(wt +yu – j вх + j 23);
где Ubdm = I1m× 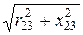 = 10
= 10 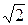 ×
× 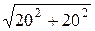 = 400 B;
= 400 B;
j 23= arctg 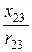 = arctg
= arctg 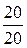 =45°,
=45°,
или ubd(t) = 400×sin(wt – 90° + 45°+ 45°) = 400×sin(wt) B.
действующие значения напряжения эквивалентного участка и токов параллельных ветвей
Ubd = 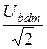 =
= 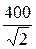 = 282 B; I2 =
= 282 B; I2 = 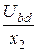 =
= 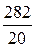 = 14,1 А;
= 14,1 А;
I3 = 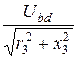 =
= 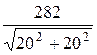 = 10 А.
= 10 А.
Углы сдвига фаз напряжений и токов второй и третьей ветвей
j 2 = arctg 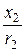 = arctg
= arctg 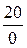 = 90°, j 3 = arctg
= 90°, j 3 = arctg 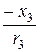 = arctg
= arctg 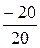 = -45°.
= -45°.
Мгновенные значения токов параллельных ветвей
i2(t) = I2 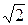 ×sin(wt+yubd – j 2) = 20×sin(wt – 90°) А;
×sin(wt+yubd – j 2) = 20×sin(wt – 90°) А;
i3(t) = I3 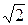 ×sin(wt+yubd – j 3) = 10
×sin(wt+yubd – j 3) = 10 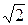 ×sin(wt + 45°) А;
×sin(wt + 45°) А;
где yubd = yu – j вх – j 23 = -90° + 45° + 45° = 0.
Проверим баланс активных мощностей: U×I1×cosj вх = I12×r1 + I32×r3.
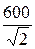 ×10×cos(-45°) = 102×10+102×20 или 3000 Вт = 3000 Вт.
×10×cos(-45°) = 102×10+102×20 или 3000 Вт = 3000 Вт.
Проверим баланс реактивных мощностей:
U×I1×sinj вх = I12×(-x4) + I22×x2 + I32×(-x3).
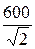 ×10×sin(-45°)=102×(-50)+(10
×10×sin(-45°)=102×(-50)+(10 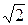 )2×20+102×(-20) или -3000 вар = -3000 вар.
)2×20+102×(-20) или -3000 вар = -3000 вар.
 Вывод: балансы активных и реактивных мощностей сходятся, следовательно, задача решена верно и можно переходить к построению полной векторной диаграммы.
Вывод: балансы активных и реактивных мощностей сходятся, следовательно, задача решена верно и можно переходить к построению полной векторной диаграммы.
Рассчитаем неизвестные напряжения на элементах электрической цепи.
Uab = I1×r1= 10×10 = 100 В; Ubc = I3×r3= 10×20 = 200 В;
Uca = I3×x3= 10×20 = 200 В; Ude = I1×x4= 10×50 = 500 В.
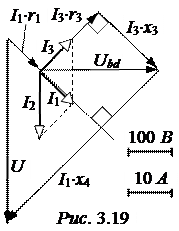
Векторная диаграмма приведена на рис. 3.19. Её построение начинается с выбора масштабов напряжений и токов. Затем в произвольном направлении строится вектор напряжения на параллельно включенных ветвях Ubd, от которого под углами j 2, j 3, j 23 строятся векторы токов I2, I3 и I1, соответственно. При этом следует учесть, что I1 = I2 + I3.
 Остальные векторы напряжений строятся в соответствии с уравнениями второго закона Кирхгофа и порядком расположения элементов эквивалентной схемы (см. рис. 3.18,б):
Остальные векторы напряжений строятся в соответствии с уравнениями второго закона Кирхгофа и порядком расположения элементов эквивалентной схемы (см. рис. 3.18,б):
Uab + Ubd + Ude = U.
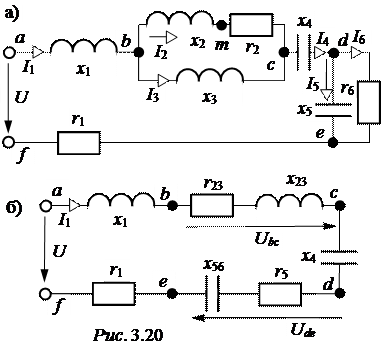
ЗАДАЧА 3.21. Рас-считать действующие значе-ния напряжений и токов в схеме рис. 3.20,а, проверить балансы активных и реак-тивных мощностей, постро-ить полную векторную диаг-рамму напряжений и токов, если: U = 300 B; r2 = 30 Ом, x2 =10 Ом; x3 = 33,33 Ом; x4 = 2 Ом;
x5 = 20 Ом; r6 = 10 Ом; x1 = 8 Ом; r1 = 4 Ом.
Решение
В рассматриваемой схеме два разветвления: на участке bc параллельно включены 2я и 3я ветви, которые могут быть заменены эквивалентной ветвью r23-x23 (рис. 3.20,б); на участке de параллельно включены 5я и 6я ветви, заменяемые последовательной эквивалентной цепью r56-x56. Замена осуществляется на основании соотношений между активными и реактивными проводимостями параллельных ветвей:
g2 = 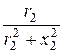 =
= 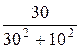 = 0,03 Cм; b2 =
= 0,03 Cм; b2 = 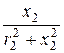 =
= 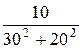 = 0,01 Cм (инд.);
= 0,01 Cм (инд.);
g3 = 0; b3 = 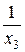 =
= 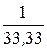 = 0,03 Cм (инд.);
= 0,03 Cм (инд.);
g23 = g2 + g3 = 0,03 + 0 = 0,03 Cм; b23 = b2 + b3 = 0,01 + 0,03 = 0,04 Cм (инд.);
r23 = 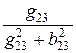 =
= 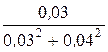 = 12 Ом;
= 12 Ом;
x23 = 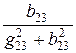 =
= 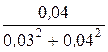 = 16 Ом (инд.).
= 16 Ом (инд.).
g5 = 0; g6 = 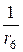 =
= 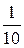 = 0,1 Cм; b5 =
= 0,1 Cм; b5 = 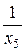 =
= 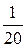 = 0,05 Cм (ёмк.); b6 = 0;
= 0,05 Cм (ёмк.); b6 = 0;
g56 = g5 + g6 = 0 + 0,1 = 0,1 Cм; b56 = b5 + b6 = 0,05 + 0 = 0,05 Cм (ёмк.);
r56 = 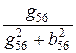 =
= 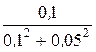 = 8 Ом; x56 =
= 8 Ом; x56 = 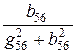 =
= 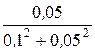 = 4 Ом (ёмк.).
= 4 Ом (ёмк.).
Входное сопротивление цепи по эквивалентной схеме (рис. 3.20,б)
Zвх = 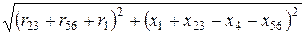
= 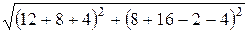 = 30 Ом;
= 30 Ом;
cosj вх = 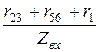 =
= 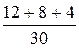 = 0,8;
= 0,8;
sinj вх = 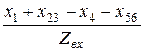 =
= 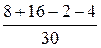 = 0,6.
= 0,6.
Ток в общей части схемы I1 = I4 = 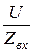 =
= 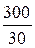 = 10 A,
= 10 A,
напряжения на разветвлениях Ubc = I1× 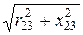 = 10
= 10 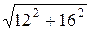 = 200 B,
= 200 B,
Ude = I1× 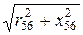 = 10
= 10 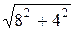 = 40
= 40 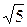 B,
B,
токи в остальных ветвях
I2 = 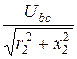 =
= 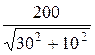 = 2
= 2 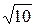 A, I5 =
A, I5 = 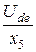 =
= 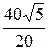 = 2
= 2 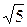 A,
A,
I3 = 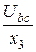 =
= 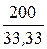 = 6 A, I6 =
= 6 A, I6 = 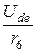 =
= 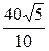 = 4
= 4 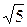 A.
A.
Проверим балансы мощностей. Баланс активных мощностей представляется для схемы рис. 3.20,а выражением
U×I1×cosj вх = I12×r1 + I22×r2 + I62×r6,
300×10×0,8 = 102×4+ 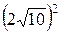 ×30+
×30+ 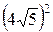 ×30
×30
или 3000 Вт = 3000 Вт - выполняется.
Баланс реактивных мощностей цепи
U×I1×sinj вх = I12×x1 + I22×x2 + I32x3 – I42×x4 – I52×x5,
300×10×0,6 = 102×8 + 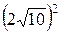 ×10 + 62×33,33 – 102×2 –
×10 + 62×33,33 – 102×2 – 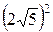 ×20
×20
или 1800 вар = 800 + 400 + 1200 – 200 – 400 вар - выполняется.
Так как оба баланса мощностей выполняются, задача расчёта цепи решена верно, и можно переходить к построению векторной диаграммы.
Так как в схеме рис. 3.20,а имеется два разветвления, то сначала строится векторная диаграмма для последовательной эквивалентной схемы рис. 3.20,б и построение начинается с выбора произвольного направления вектора тока I1 последовательной цепи (горизонтально, вправо) (рис. 3.21).
Уравнение по второму закону Кирхгофа запишем в векторной форме с соблюдением принципа: падения напряжений на элементах схемы строго следуют в соответствии с расположением элементов, и каждому вектору напряжения присваиваются соответствующие индексы точек схемы:
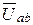 +
+ 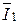 ×r23+
×r23+ 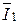 ×x23+
×x23+ 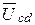 +
+ 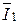 ×r56+
×r56+ 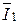 ×x56+
×x56+ 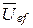 =
= 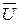 =
= 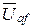 .
.
При этом 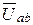 =
= 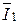 ×x1=10×8 = 80 B и этот вектор напряжения опережает ток
×x1=10×8 = 80 B и этот вектор напряжения опережает ток 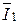 на 90°;
на 90°;
I1×r23= 10×12 = 120 B, I1×x23= 10×16 = 160 B,
Ucd = I1×x4= 10×2 = 20 B, I1×r56= 10×8 = 80 B,
I1×x56= 10×4 = 40 B, I1×r1= Uef = 10×4 = 40 B.
На рис. 3.21 падения векторных напряжений 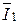 ×r23,
×r23, 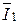 ×x23,
×x23, 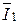 ×r56,
×r56, 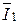 ×x56
×x56
построены пунктирно, так как эти напряжения отсутствуют в исходной схеме.
Далее переходим к построению векторов токов I2 и I3. Ток I3 перпендикулярен напряжению Ubc, а ток 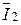 =
= 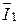 -
- 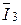 .
.
Параллельно вектору Ude откладывается ток I6, а ток 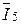 =
= 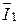 -
- 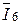 стро-ится в соответствии с первым законом Кирхгофа.
стро-ится в соответствии с первым законом Кирхгофа.
 |
Затем относительно тока I2 откладываются векторы падений напряжений
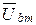 =
= 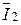 ×x2 и
×x2 и 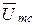 =
= 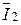 ×r2.
×r2.
Векторная диаграмма принимает окончательный вид рис. 3.21. На этой векторной диаграмме указан также вектор напряжения 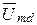 .
.
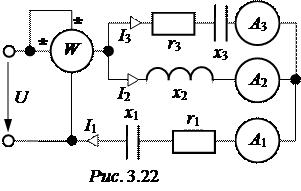 ЗАДАЧА 3.22. В схеме рис. 3.22 известно:
ЗАДАЧА 3.22. В схеме рис. 3.22 известно:
U = 200 B; r1 = 30 Ом; x1 = 50 Ом;
x2 = 10 Ом; r3 = 5 Ом; x3 = 15 Ом.
Определить показания приборов.
Решение
1. Заменяем параллельное соеди-нение ветвей 2 и 3 эквивалентным последовательным соединением сопротивлений r23 и x23:
g2 = 0; b2 = 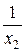 =
= 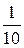 = 0,1 Cм; Z3 =
= 0,1 Cм; Z3 = 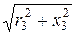 =
= 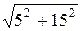 =
= 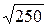 = 5
= 5 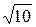 Oм;
Oм;
g3 = 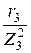 =
= 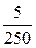 = 0,02 Cм; b3 =
= 0,02 Cм; b3 = 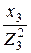 =
= 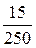 = 0,06 Cм;
= 0,06 Cм;
g23 = g2 + g3 = 0 + 0,02 = 0,02 Cм; b23 = b2 – b3 = 0,1 – 0,06 = 0,04 Cм;
Y23 = 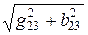 =
= 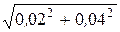 = 0,02
= 0,02 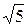 Cм; Z23 =
Cм; Z23 = 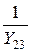 =
= 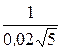 = 10
= 10 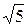 Oм;
Oм;
r23 = 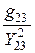 =
= 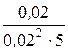 = 10 Ом; x23 =
= 10 Ом; x23 = 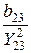 =
= 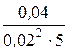 = 20 Ом.
= 20 Ом.
2. Входное сопротивление цепи и её коэффициент мощности:
Z = 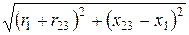 =
= 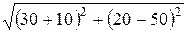 = 50 Oм;
= 50 Oм;
cosj = 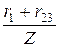 =
= 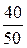 = 0,8.
= 0,8.
Действующее значение тока в неразветвлённой части цепи (показание первого амперметра): I1 = 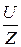 =
= 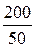 = 4 A.
= 4 A.
Напряжение на зажимах параллельных ветвей:
U23 = Z23×I1= 10 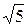 ×4 = 40
×4 = 40 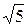 B.
B.
Показания второго и третьего амперметров:
I2 = 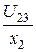 =
= 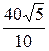 = 4
= 4 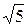 A; I3 =
A; I3 = 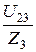 =
= 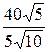 = 4
= 4 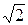 A.
A.
3. Ваттметр включен на измерение активной мощности цепи. Его показание:
P = U×I1×cosj = 200×4×0,8 = 640 Вт.
Активная мощность резисторов
PR = r1×I12 + r2×I22 = 30×42 + 5× 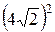 = 640 Вт
= 640 Вт
равна активной мощности источника, то есть налицо выполнение баланса активных мощностей.
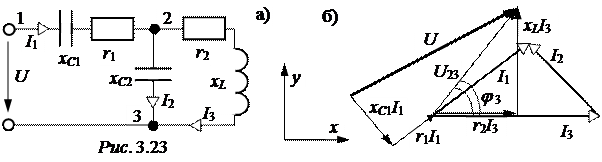
ЗАДАЧА 3.23. В схеме рис. 3.23,а известно: u(t) =100 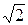 ×sin(wt+30°) B;
×sin(wt+30°) B;
r1 = 5 Ом; xC1 = 8 Ом; r2 = 3 Ом; xC2 = 10 Ом; xL = 4 Ом.
Определить токи, коэффициент мощности, построить полную векторную диаграмму цепи. Задачу решить методом пропорциональных величин. Дополнительно ответить на вопросы: при каком xC2 будет резонанс токов? При каком xC1 будет резонанс напряжений?
 |
Решение
1. Построим качественно векторную диаграмму (ВД) (рис. 3.23,б). Построение следует начинать с самого дальнего от источника участка цепи (это – третья ветвь). Поскольку здесь имеется последовательное соединение сопротивлений, сначала строим вектор тока I3. Далее построение диаграммы ведётся от конца схемы к началу (источнику) с соблюдением законов Кирхгофа и правил построения ВД.
2. Расчёт выполняем в том же порядке, в каком строилась ВД.
Пусть I3 = 1 A, т.е. i3(t) = 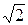 ×sin(wt) A. Тогда
×sin(wt) A. Тогда
Ur2 = r2×I3 = 3 B, UxL = xL×I3 = 4 B, I2 = 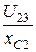 =
= 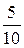 = 0,5 A.
= 0,5 A.
Проекции векторов токов на оси х и у:
I3x = I3 = 1 A, I3y = 0; j 3 = arctg 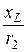 = arctg
= arctg 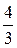 = 53,1°,
= 53,1°,
I2x = I2×cos(j 3 + 90°)= 0,5×(-0,8) = -0,4 A, I2y = I2×sin(j 3 + 90°)= 0,5×0,6 = 0,3 A.
Определяем первый ток по проекциям:
I1x = I2x + I3x = -0,4 + 1 = 0,6 A, I1y = I2y + I3y = 0,3 A,
I1 = 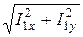 =
= 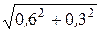 = 0,671 A.
= 0,671 A.
Фаза первого тока yi1 = arctg 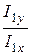 = arctg
= arctg 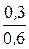 = 26,6°.
= 26,6°.
Определяем расчётное значение входного напряжения по проекциям:
UxC1 = xC1×I1 = 8×0,671 = 5,36 B; Ur1 = r1×I1 = 5×0,671 = 3,35 B,
Ux = UxC1×cos( 90° – yi1) + Ur1×cos(yi1) + Ur2 =
= 5,36×cos(90° – 26,6°) + 3,35×cos(26,6°) + 3 =8,40 B,
Uy = UxC1×sin(yi1 – 90°) + Ur1×sin(yi1) + UxL =
= 5,36×sin(26,6° – 90°) + 3,35×sin(26,6°) + 4 =0,707 B,
Uрасч = 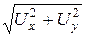 =
= 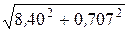 = 8,43 B,
= 8,43 B,
yUрасч = arctg 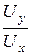 = arctg
= arctg 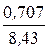 = 4,8°.
= 4,8°.
3. Коэффициенты пересчёта:
k = 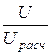 =
= 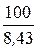 = 11,86; Dy =yU – yUрасч = 30° – 4,8° = 25,2°.
= 11,86; Dy =yU – yUрасч = 30° – 4,8° = 25,2°.
4. Получаем ответы i1(t) = 7,96 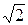 ×sin(wt + 51,8°) A;
×sin(wt + 51,8°) A;
i2(t) = 5,93 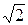 ×sin(wt + 168,4°) A;
×sin(wt + 168,4°) A;
i3(t) = 11,86 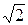 ×sin(wt + 25,2°) A.
×sin(wt + 25,2°) A.
5. Условие резонанса токов: b2= b3.
b2= 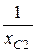 ; b3=
; b3= 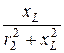 =
= 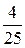 См; хС2 =
См; хС2 = 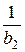 =
= 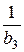 =
= 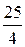 = 6,25 Ом.
= 6,25 Ом.
6. Условие резонанса напряжений хС1= х23,
но Z23= 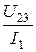 =
= 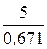 = 7,46 Ом,
= 7,46 Ом,
х23 = Z23×sin(j 3 – yi1) = 7,46×sin(53,1° –26,6°) = 3,33 Ом.
Таким образом, резонанс напряжений наблюдается при хС1= 3,33 Ом.
Дата добавления: 2016-01-18; просмотров: 1754;
