Статистические ряды распределения и их графическое изображение
В результате группировки единиц совокупности по какому-либо признаку получают ряды распределения.
Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
В более широком смысле ряд распределения – это первичная характеристика массовой статистической совокупности, в которой находят количественное выражение закономерности массовых явлений и процессов общественной жизни.
Ряды распределения дают возможность:
а) проследить закономерность распределения;
б) судить об однородности совокупности и границах ее вариации;
в) исчислить различные обобщающие показатели (среднюю, моду, дисперсию и т.д.).
Ряды распределения могут быть построены по различным признакам:
- по атрибутивному – атрибутивные ряды распределения;
- по количественному – вариационные ряды распределения.
Ряды распределения (вариационные) состоят из 2-х элементов:
- вариант (х);
- частот (f).
Вариантами (х) называются отдельные значения признака.
Частотами (f) называются величины, показывающие, сколько раз повторяется данная варианта.
Иногда частоты могут выражаться в относительных величинах: долях единицы или в процентах. Тогда их называют частости.
Сумму всех частот (Σf) называют объемом ряда распределения или численностью (объемом) совокупности и обозначают N (n).
Σf = 1, если это частости, выраженные в долях единицы;
Σf = 100, если это частости, выраженные в процентах;
Σf = N (n) – численность совокупности (N – генеральной, n – выборочной).
В зависимости от характера вариации признака вариационные ряды могут быть:
а) дискретными, когда величина признака принимает целочисленные значения.
Например:
Количество детей в семье Число семей
х f
0 100
1 120
2 110
3 50
4 5
5 2
6 1
б) интервальными, когда величина признака представлена в виде интервалов (как правило, непрерывный признак, но не обязательно).
Например:
Балл успеваемости студента Число студентов
х f
4 – 6 15
6 – 8 20
8 – 10 35
Порядок построения дискретного ряда распределения следующий:
1) ряд данных ранжируют, т.е. располагают в порядке возрастания или убывания;
2) считают число повторений каждого значения признака, т.е. частоту.
Например, имеются сведения об оценках, полученных на экзамене по статистике студентами группы (24 чел.):
| Поряд.№ студента в списке | |||||||||||||
| Оценка, х | |||||||||||||
| № | |||||||||||||
| х |
1. Ранжируем уровни ряда (в порядке возрастания):
х : 2, 3, 4, 4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 10, 10.
2. Строим дискретный ряд распределения (т.к. признак – прерывный):
| х | ||||||||||
| f | Σf = 24 |
При построении интервальных рядов порядок действий следующий:
1) определяют число групп,
2) определяют ширину интервала,
3) считают число значений признака, попадающих в каждый интервал.
Например, в нашем примере:
1) n = 24, следовательно, по формуле Стерджесса число групп К = 5;
2) ширина интервала 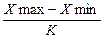 =
= 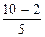 = 1,6;
= 1,6;
3) строим интервальный ряд (таблица 3.11):
Таблица 3.11 – Группировка студентов по успеваемости
| Оценка на экзамене, х | Число студентов, f |
| 2,0 – 3,6 | |
| 3,6 – 5,2 | |
| 5,2 – 6,8 | |
| 6,8 – 8,4 | |
| 8,4 – 10,0 | |
| Всего | Σf = 24 |
Для графического изображения рядов распределения широко применяются линейные и плоскостные диаграммы.
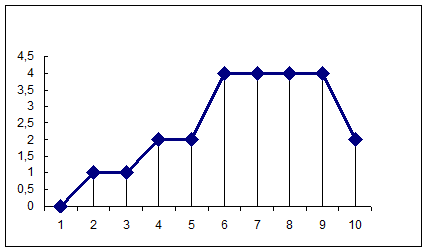
Так, для изображения дискретных вариационных рядов используется полигон.
При этом на оси абсцисс откладываются значения признака (х), на оси ординат – частоты (f). В местах их пересечения ставятся точки, которые затем соединяются ломаной линией (полигоном).
|
 | |||||
| |||||
 | |||||
Рисунок 3.2 – Полигон распределения оценок, полученных на экзамене по статистике
Для изображения интервальных рядов распределения обычно используют гистограммы. На оси абсцисс откладывают интервалы признака, на оси ординат – частоты и строят прямоугольники (основание прямоугольника – ширина интервала, высота – соответствующая частота).
В нашем примере:
|
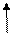





|
Рисунок 3.3 – Гистограмма распределения оценок, полученных на экзамене по статистике
Если интервалы в интервальном ряду неравные, то при построении гистограммы на ось ординат наносится плотность распределения – частота, рассчитанная на единицу ширины интервала.
Если на графике (рисунок 3.3) соединить ломаной линией центры интервалов, то получится полигон распределения для интервального ряда.
Ряды распределения могут также изображаться с помощью кумуляты (кумулятивной кривой или кривой сумм). На оси абсцисс – значения признака, на оси ординат – накопленные частоты. Накопленные частоты определяются последовательным суммированием по группам. Они показывают, сколько единиц совокупности имеют значения признака не большее, чем рассматриваемое значение.
Например, наш вариационный ряд (дискретный):
| x | f | Накопленная частота |
| 2 (1+1) 4 (1+1+2) 6 (1+1+2+2) и т.д. | ||
| ∑f = 24 |
|

|
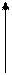
Рисунок 3.4 – Кумулята распределения оценок, полученных на экзамене по статистке
Помимо указанных способов графического изображения рядов распределения, некоторые авторы указывают на возможность использования для этих целей огивы. Однако существуют разные точки зрения. Так, в [15] отмечается, что огиву можно получить, если на оси ординат не частоты, а частости. А в [1] авторы указывают, что огива получается, если при графическом изображении кумуляты поменять местами оси.
Дата добавления: 2016-01-16; просмотров: 1158;
