ПРОЕКТИРОВАНИЕ И АНАЛИЗ ЧАСТОТНО-ИЗБИРАТЕЛЬНЫХ ФИЛЬТРОВ С ПРИМЕНЕНИЕМ САПР

5.1. Классификация и основные характеристики фильтров

Электрический фильтр – это частотно-избирательное устройство, изменяющее амплитудный или фазовый спектр сигнала.

Характеристику частотно-избирательного фильтра в частотной области принято описывать при помощи передаточной функции W(p).

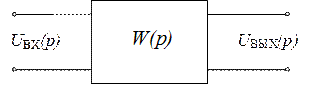
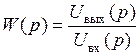
Рис. 5.1. Частотно-избирательный фильтр как четырехполюсник

На рис. 5.1 как U_вх(p) и U_вых(p) обозначены р-изображения входного и выходного сигналов, полученные путем прямого непрерывного преобразования Лапласа:

.

АЧХ фильтра – это модуль передаточной функции |W(jw)|, а фазочастотная характеристика (ФЧХ) – это аргумент передаточной функции j(w) .

АЧХ определяет фильтрующие свойства по амплитуде: составляющие сигнала, имеющие различные частоты, будут ослабляться фильтром в разной степени.

ФЧХ характеризует фильтрующие свойства по фазе: составляющие сигнала, имеющие различные частоты, будут сдвигаться фильтром по фазе в разной степени.

По виду амплитудно-частотной характеристики (АЧХ) различают 4 основных вида фильтров (рис. 5.2):

- фильтр нижних частот (ФНЧ) – пропускает НЧ от 0 Гц и задерживает ВЧ;

- фильтр верхних частот (ФВЧ) – пропускает ВЧ и задерживает НЧ;

- полосно-пропускающий фильтр (ППФ) – пропускает полосу частот и подавляет частоты выше и ниже этой полосы;

- полосно-заграждающий фильтр (ПЗФ) – подавляет определенную полосу частот и пропускает частоты выше и ниже этой полосы.

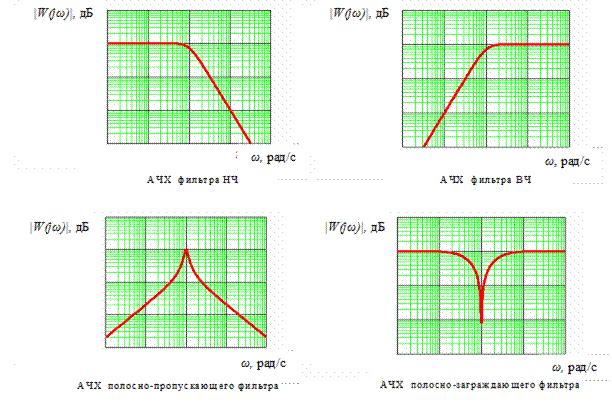Рис. 5.2. Амплитудно-частотные характеристики (АЧХ)
основных видов фильтров

Для возможности анализа формы АЧХ в широких диапазонах изменения коэффициентов передачи и частот, АЧХ, как правило, представляют в логарифмическом масштабе (т.н. логарифмическая АЧХ, или ЛАЧХ):

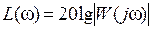, дБ.

Также возможно представление АЧХ в виде затухания для нормированной АЧХ (имеющей единичный коэффициент передачи в полосе пропускания):

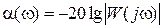, дБ.

ЛАЧХ ФНЧ, выраженные через коэффициент передачи и через
затухание, показаны на рис. 5.3; ЛАЧХ идеального и реального фильтров нижних частот показаны на рис. 5.4.

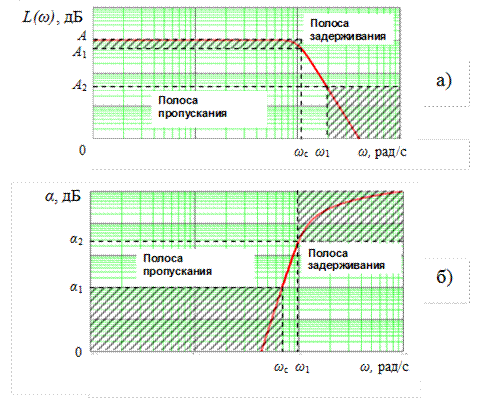
Рис. 5.3. ЛАЧХ ФНЧ: а – через коэффициент передачи;
б - через затухание

Частота среза ω_с – это частота, на которой происходит сопряжение областей пропускания и задерживания. Для идеального с точки зрения АЧХ ФНЧ полоса задерживания начинается сразу за полосой пропускания, т.е. отсутствует переходная область АЧХ.

В фильтрах с монотонной АЧХ для определения частоты среза используют критерий «половинной мощности», согласно которому на частоте среза квадрат АЧХ должен быть равен половине своего максимального значения в полосе пропускания. Иными словами, ω_с таких фильтров определяется как частота, на которой АЧХ уменьшается в 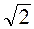раз (или на 3 дБ) по отношению к ее максимальному значению в полосе пропускания.

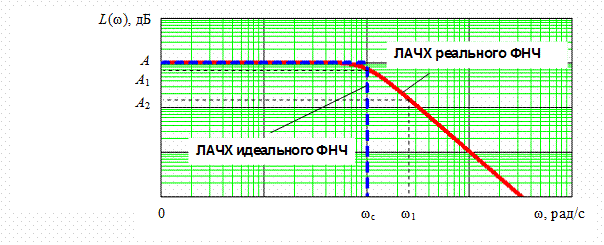
Рис. 5.4. ЛАЧХ фильтра нижних частот: 0¸w_с – полоса пропускания;
w_с¸ w₁ – переходная область; w₁¸ ¥ – полоса задерживания

В полосе пропускания затухание никогда не превышает значение α₁ = 3 дБ. Минимальное значение затухания α₂, соответствующее началу полосы задерживания, в зависимости от требований, предъявляемых к ФНЧ, может находиться в диапазоне 20…100 дБ.

Коэффициент усиления ФНЧ k – это значение модуля коэффициента передачи при ω=0.

С помощью физически реализуемых фильтров невозможно построить ФНЧ с идеальной АЧХ, но можно максимально приблизить реальную АЧХ к идеальной. Передаточная функция реализуемого фильтра представляет собой отношение полиномов:

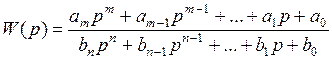. (5.1)

Фильтры, у которых все коэффициенты 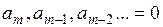, кроме a₀, называются полиномиальными. Порядок фильтра определяется максимальной степенью n знаменателя передаточной функции. Чем выше n, тем ближе АЧХ к идеальной. Однако при высоких n увеличиваются аппаратные затраты на реализацию фильтра и, как правило, ухудшаются его динамические свойства.

Фильтр физически реализуем, если выполнены следующие условия:

1) полюсы должны иметь отрицательные действительные части,

2) старшая степень n полинома в знаменателе должна быть больше или равна старшей степени m полинома в числителе.

Большинство типов фильтров имеет нелинейную ФЧХ, что допустимо во многих областях применения. Однако существуют задачи, где требуется линейная ФЧХ (радиолокация, телевидение, аудиотехника, обработка речевых сообщений).

Групповое время задержки (время замедления)

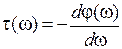. (5.2)

характеризует фазовые искажения, вносимые фильтром на разных частотах (время задержки фильтром максимума передаваемой энергии). С точки зрения ФЧХ идеальным считается фильтр, имеющий постоянное групповое время задержки в полосе пропускания, и, следовательно, линейную ФЧХ (этому условию удовлетворяют фильтры нижних частот Бесселя). Такие фильтры не вносят в сигнал линейных искажений – изменений формы сложного сигнала во времени, вызываемых различными условиями передачи его гармонических составляющих.

ФЧХ идеального и реального фильтров нижних частот показаны на рис. 5.5.

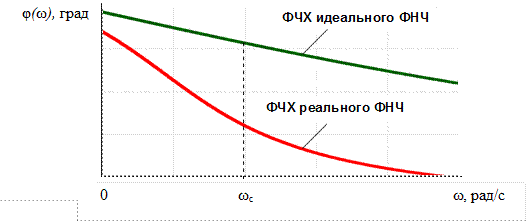
Рис. 5.5. ФЧХ фильтра нижних частот

Общим свойством фильтров нижних частот является то, что при улучшении АЧХ (повышении избирательности) фазочастотная характеристика будет ухудшаться (становиться нелинейной).

5.2. Проектирование фильтров

Проектирование фильтра производится с учетом одного или нескольких из следующих требований:

1) форма АЧХ должна обеспечивать частотную избирательность (требуемое отношение «сигнал/помеха» на выходе фильтра);

2) в случае, сигнал широкополосный (т.е. содержит набор гармоник), форма ФЧХ в полосе пропускания должна быть близка к линейной;

3) время установления выходного сигнала фильтра должно быть минимальным, а переходный процесс – иметь малую амплитуду перерегулирований;

4) аппаратные затраты на реализацию схемы фильтра должны быть минимальны.

При проектировании фильтров, в зависимости от задачи, стремятся к наилучшему приближению (аппроксимации) идеальных частотных характеристик (АЧХ либо ФЧХ). Следует отметить, что одновременная аппроксимация и АЧХ, и ФЧХ невозможна.

Необходимо выбрать такие коэффициенты полиномов числителя и знаменателя передаточной функции, которые обеспечат не только аппроксимацию выбранной частотной характеристики, но и физическую реализуемость фильтра. Применительно к квадрату АЧХ это означает выполнение следующих условий:

1) полиномы числителя и знаменателя должны быть полиномами от ω²;

2) коэффициенты полиномов должны быть ве

щественными числами;

3) значения полиномов должны быть положительны для всех ω>0 .

Известно довольно много аппроксимаций, отвечающих этим условиям, однако наибольшее распространение получили аппроксимации АЧХ Баттерворта, Чебышева, инверсная Чебышева, Кауэра (эллиптическая) и аппроксимации ФЧХ Бесселя и Гаусса.

Все эти аппроксимации предназначены для ФНЧ, но довольно просто могут быть преобразованы в аппроксимации других типов фильтров.

5.2.1. ФНЧ Баттерворта

Фильтр нижних частот Баттерворта обладает монотонной АЧХ, никогда не возрастающей с увеличением частоты, наиболее близкой к идеальной горизонтали на низких частотах (рис. 5.6). Частота среза ω_с фильтра Баттерворта определяется по относительному уровню
A₁= – 3 дБ (т.е. по уровню затухания 3 дБ).

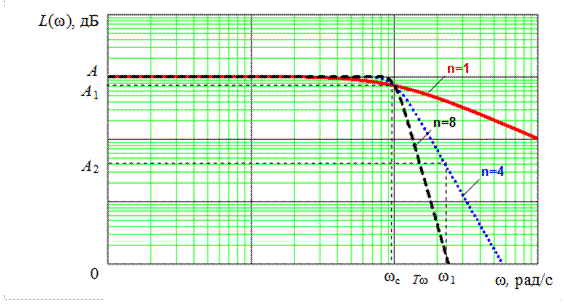
Рис. 5.6. ЛАЧХ ФНЧ Баттерворта: n – порядок фильтра;
T_w=w₁ – w_c – переходная область АЧХ

Для нормированного фильтра, т.е. при значении w_c, равном
1 рад/cек, передаточную функцию ФНЧ Баттерворта можно записать в виде произведения сомножителей для n = 2, 4, 6...

,

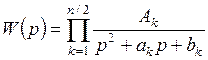или для n = 1, 3, 5...

.

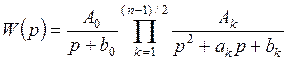В обоих случаях коэффициенты задаются при b₀ = 1 и для
k = 1, 2,... следующим образом:

.

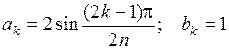АЧХ ФНЧ Баттерворта описывается следующим выражением:

,

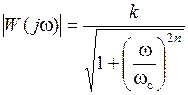где k – коэффициент усиления; n – порядок фильтра.

Увеличение порядка n ФНЧ приближает АЧХ к идеальной. Для низкочастотного диапазона АЧХ фильтра Баттерворта наилучшим образом аппроксимирует идеальную АЧХ ФНЧ.

ЛАЧХ ФНЧ Баттерворта описывается функцией:

.

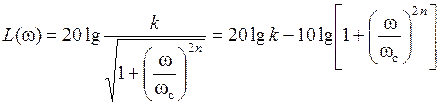Для нормированной АЧХ k = 1, отсюда:

, , .

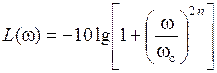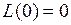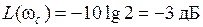Найдем порядок n_тр ФНЧ Баттерворта, требуемый для реализации заданной АЧХ. Для этого необходимо выразить значение n из логарифмической частотной характеристики:

; ;

; ;

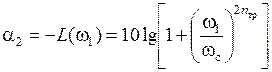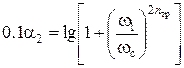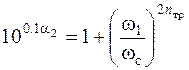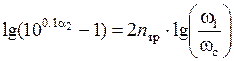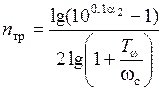, (5.3)

где 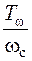– нормированная ширина переходной области АЧХ.

5.2.2. ФНЧ Чебышева

ФНЧ Чебышева представляет собой оптимальный полиномиальный фильтр. При данном порядке n и допустимом отклонении коэффициента передачи k от заданного в полосе пропускания он обеспечивает минимальную ширину переходной области АЧХ и превосходит в этом отношении фильтр Баттерворта. ЛАЧХ ФНЧ Чебышева показана на рис. 5.7.

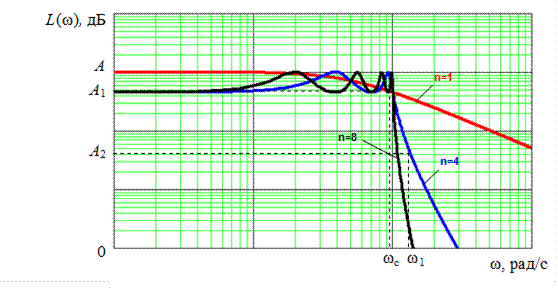
Рис. 5.7. ЛАЧХ ФНЧ Чебышева

АЧХ ФНЧ Чебышева описывается следующим выражением:

,

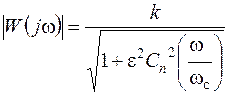где ε и k – постоянные числа, С_n(x) – полином Чебышева первого рода степени n:

,

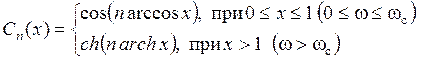где n – порядок фильтра.

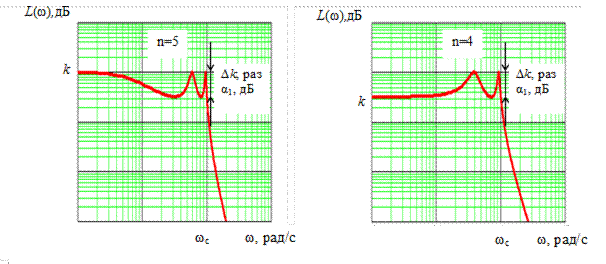
Величиной ε определяется неравномерность коэффициента передачи вполосе пропускания (см. рис. 5.8):

.

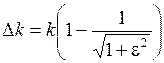а)	б)

Рис. 5.8. ЛАЧХ ФНЧ Чебышева: а) – нечетного порядка; б) – четного порядка.

Для нечетного n частота среза ω_сопределяется по уровню затухания АЧХ α₁ дБ (или Dk раз), а для четного n – по уровню 0 дБ (или
1 раз) относительно коэффициента усиления на постоянном токе k.

ЛАЧХ ФНЧ Чебышева описывается функцией:

.

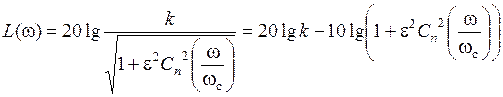Для нормированной АЧХ (k = 1):

.

.

.

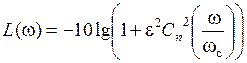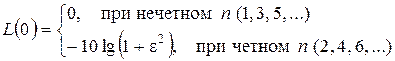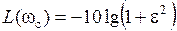Для нахождения требуемого порядка n_тр ФНЧ Чебышева запишем:

;

;

.

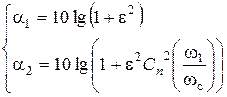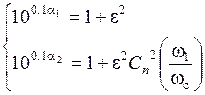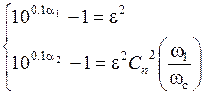Разделив второе уравнение системы на первое, извлекаем квадратный корень из правой и левой частей:

;

; ;

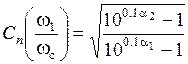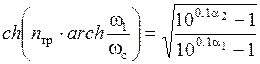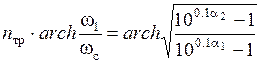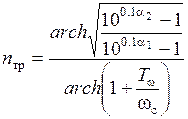. (5.4)

5.2.3. ФНЧ Бесселя

Фильтр нижних частот Бесселя отличается от других фильтров тем, что имеет оптимальную фазочастотную характеристику с точки зрения неискаженной передачи сигнала в полосе пропускания. Проходящий через фильтр сигнал не изменит своей формы, если все гармоники сигнала будут задерживаться в фильтре на одно и то же время, т.е. ФЧХ фильтра будет иметь линейный характер. Фильтр Бесселя обеспечивает наилучшее приближение реальной ФЧХ к идеальной линейной зависимости, но имеет меньший наклон АЧХ в полосе подавления и переходной области, чем фильтры Баттерворта и Чебышева. Частота среза фильтра Бесселя определяется не по АЧХ, а по излому характеристики группового времени задержки τ(ω), пример которой изображен на рис. 5.9.

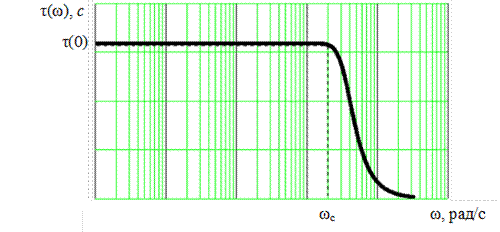
Рис. 5.9. Характеристика группового времени задержки
ФНЧ Бесселя 4-го порядка

Передаточная функция фильтра Бесселя n-го порядка имеет вид:

,

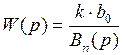где k – коэффициент усиления фильтра на постоянном токе; B_n(p) – полином Бесселя:

,

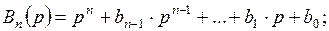
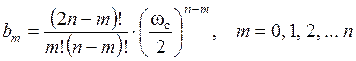где b_m – числовые коэффициенты полинома Бесселя; n – порядок фильтра, определяемый числом реактивных элементов; ω_c – частота среза ФНЧ Бесселя – предельная частота, на которой сохраняется постоянное время замедления, вносимое фильтром.

Характеристика времени замедления фильтра Бесселя максимально плоская, подобно амплитудно-частотной характеристике фильтра Баттерворта.

Для реального фильтра время замедления определяется согласно (5.2) как производная ФЧХ, взятая с отрицательным знаком. Частотная характеристика времени замедления фильтра Бесселя τ(ω) в диапазоне частот от 0 до ω_cмонотонно спадает от значения на частоте ω = 0, равного τ(0) ≈ 1/ω_c, до значения на частоте ω = ω_с, которое составляет:

для n = 2 ;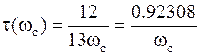

для n = 3 ;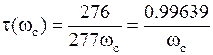

для n = 4 .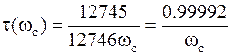

Видно, что при увеличении порядка фильтра время замедления приближается к постоянному значению. При этом обеспечиваются условия неискаженной передачи сигнала сложной формы.

Фильтр Бесселя относится к полиномиальным фильтрам нижних частот. АЧХ фильтра Бесселя монотонно спадает от расположенного на нулевой частоте максимального значения (рис. 5.10), но при этом АЧХ фильтра Бесселя уступает характеристикам фильтров Баттерворта и Чебышева, т.к. имеет меньшую крутизну спада в переходной частотной области.

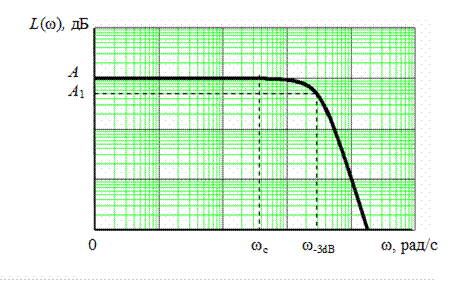
Рис. 5.10. ЛАЧХ фильтра Бесселя 4-го порядка

Для заданного времени замедления τ(0)в полосе пропускания можно приблизительно найти частоту среза ω_cФНЧ и частоту по уровню затухания АЧХ 3 дБ (для n ≥ 3):

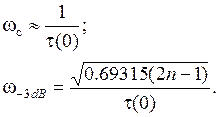
5.2.4. Инверсный и эллиптический ФНЧ Чебышева

Инверсный и эллиптический ФНЧ Чебышева относятся к классу неполиномиальных фильтров, т.е. тех, которые описываются передаточной функцией общего вида (5.1) при ненулевых коэффициентах не только знаменателя, но и числителя.

Инверсный фильтр Чебышева имеет АЧХ, которая монотонна в полосе пропускания и содержит пульсации в полосе задерживания. На рис. 5.11 показана ЛАЧХ инверсного фильтра Чебышева 4-го порядка.

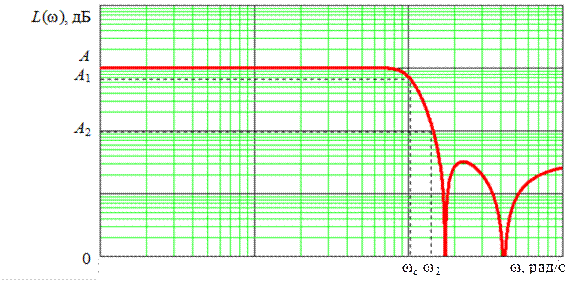
Рис. 5.11 ЛАЧХ инверсного фильтра Чебышева 4-го порядка

АЧХ инверсного ФНЧ Чебышева описывается выражением:

,

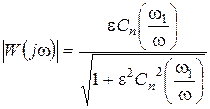где ε – постоянное число, С_n(x) – полином Чебышева первого рода степени n:

,

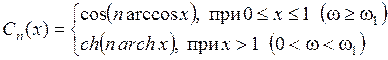где ω₁ – начальная частота полосы задерживания, n – порядок фильтра.

Величиной εопределяется неравномерность коэффициента передачи вполосе задерживания (ω ≥ ω₁):

.

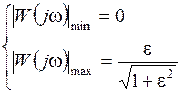Размах пульсаций составляет 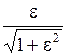, или в логарифмическом масштабе для затухания:

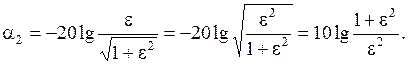
Отсюда можно определить величину ε:

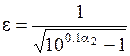. (5.5)

Частота среза ω_сдля инверсного фильтра Чебышева любого порядкаопределяется по уровню затухания 3 дБ.

Для определения требуемого порядка n_тр инверсного ФНЧ Чебышева запишем значение АЧХ на частоте ω_с (в абсолютных единицах):

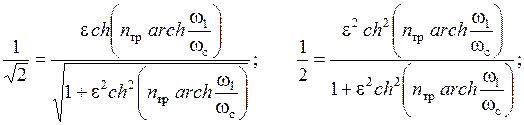
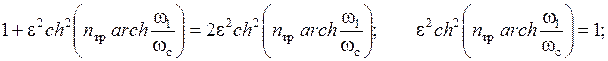
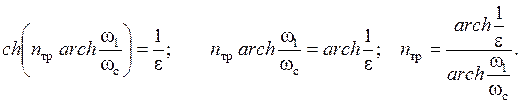
С учетом выражения (5.5) получим:

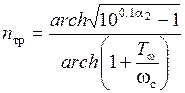. (5.6)

Анализ выражения (5.6) показывает, что требуемый порядок инверсного ФНЧ Чебышева примерно требуемому порядку ФНЧ Чебышева, имеющего допустимое затухание в полосе пропускания α₁ = 3 дБ.

Эллиптический фильтр Чебышева имеет АЧХ, содержащую пульсации как в полосе пропускания, так и в полосе задерживания. АЧХ эллиптического ФНЧ Чебышева имеет самый крутой наклон на частотах выше ω_с. На рис. 5.12 показана ЛАЧХ эллиптического фильтра Чебышева 4-го порядка.

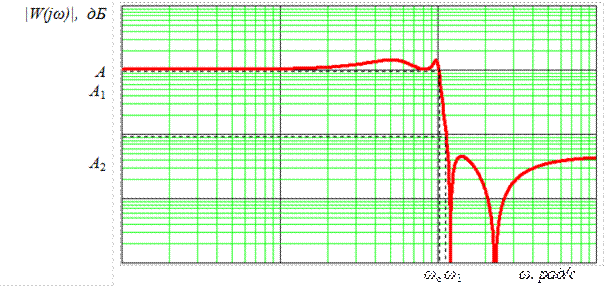Рис. 5.12. ЛАЧХ эллиптического фильтра Чебышева 4-го порядка