Передаточные функции элементарных звеньев 1-го и 2-го порядка
| Тип фильтра, функциональное обозначение | Звенья 1-го порядка | Звенья 2-го порядка | |
| Полиномиальный ФНЧ-прототип (Баттерворта, Чебышева, Бесселя) | Неполиномиальный ФНЧ-прототип (инверсный Чебышева, эллиптический Чебышева) | ||
ФНЧ

| 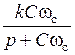
| 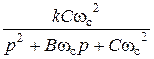
| 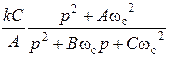
|
ФВЧ

| 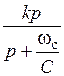
| 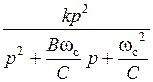
| 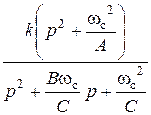
|
ППФ

| – | 
| 
|
ПЗФ

| – | 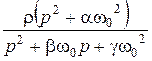
| 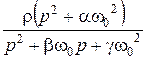
|
Возможный вид ЛАЧХ полиномиального звена ФНЧ 2-го порядка показан на рис. 5.16.

Рис. 5.16. Возможный вид ЛАЧХ полиномиального звена ФНЧ 2-го порядка
Добротность полиномиального звена ФНЧ 2-го порядка определяется по формуле: 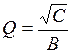 . АЧХ звена ФНЧ 2-го порядка имеет максимум только при выполнении условия
. АЧХ звена ФНЧ 2-го порядка имеет максимум только при выполнении условия 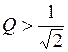 , в противном случае АЧХ монотонно убывает.
, в противном случае АЧХ монотонно убывает.
Возможный вид ЛАЧХ звена ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом показан на рис. 5.17.
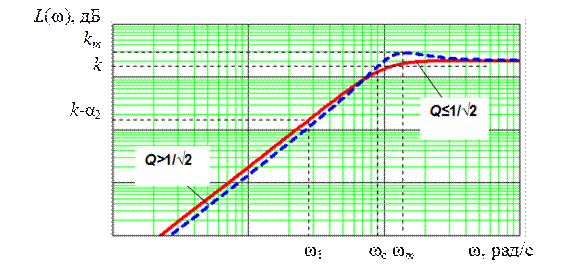
Рис. 5.17. Возможный вид ЛАЧХ полиномиального звена ФВЧ 2-го порядка
Добротность определяется по формуле: 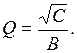 Переходная область АЧХ определяется, как разность:
Переходная область АЧХ определяется, как разность: 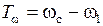 .
.
АЧХ звена ФВЧ 2-го порядка имеет максимум только при выполнении условия 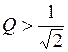 , в противном случае АЧХ монотонно возрастает.
, в противном случае АЧХ монотонно возрастает.
Возможный вид ЛАЧХ звена ППФ 2-го порядка с полиномиальным ФНЧ-прототипом показан на рис. 5.18.
 Рис. 5.18. Возможный вид ЛАЧХ звена ППФ 2-го порядка с полиномиальным ФНЧ-прототипом: ω0 – центральная частота; ωL, ωU – нижняя и верхняя частоты среза, определяемые по уровню затухания α1= 3 дБ и для ППФ Баттерворта, и для ППФ Чебышева; Δω = ωU – ωL – полоса пропускания; 0 ÷ ω1; ω2 ÷ ∞ – нижняя и верхняя полосы задерживания
Рис. 5.18. Возможный вид ЛАЧХ звена ППФ 2-го порядка с полиномиальным ФНЧ-прототипом: ω0 – центральная частота; ωL, ωU – нижняя и верхняя частоты среза, определяемые по уровню затухания α1= 3 дБ и для ППФ Баттерворта, и для ППФ Чебышева; Δω = ωU – ωL – полоса пропускания; 0 ÷ ω1; ω2 ÷ ∞ – нижняя и верхняя полосы задерживания
АЧХ ППФ имеет две боковые полосы, и две переходные области:
- нижнюю: 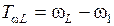 ,
,
- верхнюю: 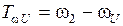 .
.
Для любой АЧХ звена ППФ выполняется соотношение:
TωU> TωL.
Добротность 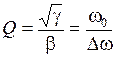 характеризует качество ППФ, т.е. его избирательность. Зависимость ЛАЧХ ППФ от добротности и порядка фильтра поясняет рис. 5.19.
характеризует качество ППФ, т.е. его избирательность. Зависимость ЛАЧХ ППФ от добротности и порядка фильтра поясняет рис. 5.19.
Коэффициент усиления ППФ k определяется как значение его АЧХ на центральной частоте ω0.
|
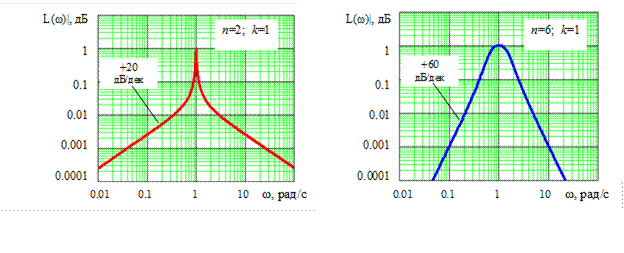 Рис. 5.19. Зависимость ЛАЧХ ППФ Баттерворта от добротности и порядка фильтра: а) – ППФ 2-го порядка с добротностью Q=40; б) – ППФ 6-го порядка с добротностью Q=1
Рис. 5.19. Зависимость ЛАЧХ ППФ Баттерворта от добротности и порядка фильтра: а) – ППФ 2-го порядка с добротностью Q=40; б) – ППФ 6-го порядка с добротностью Q=1
Возможный вид ЛАЧХ звена ПЗФ 2-го порядка с полиномиальным ФНЧ-прототипом показан на рис. 5.20.
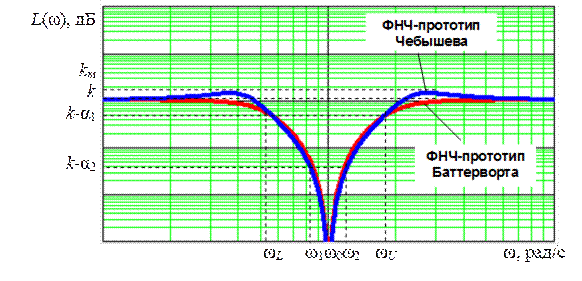 Рис. 5.20. Возможный вид ЛАЧХ звена ПЗФ 2-го порядка с полиномиальным ФНЧ-прототипом: ω0– центральная частота; ωL, ωU – нижняя и верхняя частоты среза, определяемые по уровню затухания 3 дБ и для ПЗФ Баттерворта, и для ПЗФ Чебышева; Δω = ω2 – ω1– полоса задерживания; 0 ÷ ωL ; ωU ÷ ∞ – нижняя и верхняя полосы пропускания
Рис. 5.20. Возможный вид ЛАЧХ звена ПЗФ 2-го порядка с полиномиальным ФНЧ-прототипом: ω0– центральная частота; ωL, ωU – нижняя и верхняя частоты среза, определяемые по уровню затухания 3 дБ и для ПЗФ Баттерворта, и для ПЗФ Чебышева; Δω = ω2 – ω1– полоса задерживания; 0 ÷ ωL ; ωU ÷ ∞ – нижняя и верхняя полосы пропускания
АЧХ ПЗФ имеет две боковые полосы, и две переходные области:
- нижнюю: 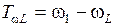 ,
,
- верхнюю: 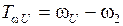 .
.
Для любой АЧХ звена ПЗФ выполняется соотношение TωU> TωL.
Добротность Q характеризует избирательность ПЗФ. Коэффициент усиления ПЗФ k определяется как значение его АЧХ на постоянном токе.
Так какдля ППФ и ПЗФ TωU> TωL, при их проектировании требуемая ширина переходной области ФНЧ-прототипа, а, следовательно, и необходимый порядок ФНЧ-прототипа, определяются по минимально допустимому значению TωU.
Дата добавления: 2015-11-26; просмотров: 2741;
