Пример расчета требуемого порядка фильтра для различных аппроксимаций ФНЧ.

Задано:

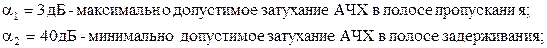
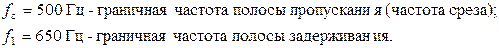
Определим ширину переходной области АЧХ: .

Требуемый порядок ФНЧ Баттерворта:

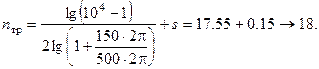
Требуемый порядок ФНЧ Чебышева:

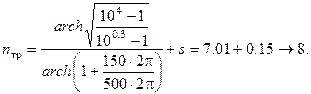
Требуемый порядок инверсного ФНЧ Чебышева:

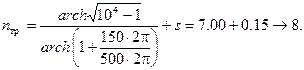
Порядок фильтра n_тр выбирается с коэффициентом запаса s=0.15, с дальнейшим округлением в сторону увеличения. Для эллиптического фильтра Чебышева (n_тр=5) и фильтра Бесселя (n_тр=29) определение требуемого порядка производится графоаналитическим или табличным способом.

В общем случае проектирование фильтра включает в себя следующие этапы:

1. Выбор аппроксимации.

2. Определение порядка фильтра.

3. Выбор структуры фильтра.

4. Расчет и выбор элементов схемы.

5. Согласование фильтра с источником сигнала и нагрузкой.

6. Схемотехническое моделирование и оптимизация схемы.

7. Макетирование и экспериментальная проверка схемы.

При проектировании фильтров, в зависимости от задачи, стремятся к наилучшему приближению (аппроксимации) идеальных частотных характеристик (АЧХ либо ФЧХ). Следует отметить, что одновременная аппроксимация и АЧХ, и ФЧХ невозможна.

Сравнение амплитудно-частотных характеристик различных аппроксимаций фильтров показано на рис. 5.13, фазочастотных характеристик – на рисунке 5.14, импульсных характеристик (рекций на
δ-импульс, или функцию Дирака) – на рисунке 5.15.

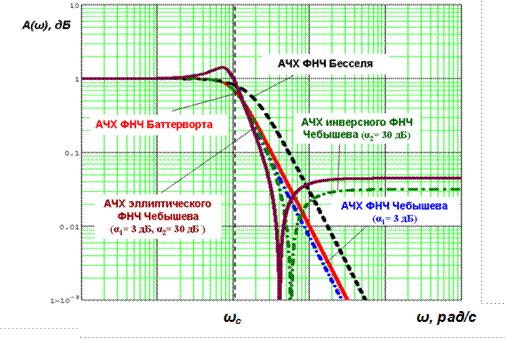
Рис. 5.13. Сравнение ЛАЧХ различных аппроксимаций ФНЧ 2-го порядка

Рис. 5.14. Сравнение ФЧХ различных аппроксимаций ФНЧ 2-го порядка

Рис. 5.15. Сравнение импульсных характеристик различных

аппроксимаций ФНЧ 2-го порядка

Практические рекомендации по использованию аппроксимаций АЧХ и ФЧХ можно сформулировать в следующем виде:

1. Если есть требование неискаженной передачи широкополосного сигнала, спектр которого находится в полосе пропускания фильтра, то следует выбрать аппроксимацию Бесселя, имеющую линейную ФЧХ. Такой же выбор следует сделать, если в техническом задании (ТЗ) есть требование минимальной длительности и «гладкой» формы переходных процессов при воздействии импульсных сигналов.

2. Если, согласно ТЗ, требуется высокая стабильность коэффициента передачи фильтра в полосе пропускания, то используется инверсная аппроксимация Чебышева.

3. Если согласно ТЗ, требуется высокая стабильность коэффициента передачи фильтра на низких частотах и большой коэффициент подавления на всех частотах выше полосы пропускания, то используется аппроксимация Баттерворта.

4. Если, согласно ТЗ, допускается неравномерность коэффициента передачи в полосе пропускания, но требуется крутой спад АЧХ на частотах выше ω_с (при отсутствии требований к линейности ФЧХ фильтра и малой длительности переходных процессов), наиболее простая реализация фильтра – с использованием эллиптической аппроксимации Чебышева (Кауэра). Она будет обеспечивать наименьший из всех рассмотренных аппроксимаций порядок фильтра. В этом же случае, если рассчитанный порядок фильтра отличается незначительно, может быть целесообразно использование аппроксимации Чебышева, так как фильтр на ее основе будет обладать лучшими динамическими характеристиками, чем фильтр Кауэра.

5.2.5. Частотные преобразования фильтров. Передаточные функции и АЧХ фильтров 1-го и 2-го порядков

В общем случае, для нормированного ФНЧ 1-го порядка (т.е. при ω_с=1 рад/с), передаточная функция представляется в виде:

, (5.7)

где C – постоянное число, а F(p) – полином нулевой или первой степени.

Для нормированного ФНЧ 2-го порядка передаточная функция имеет вид:

, (5.8)

где B и С – постоянные числа, а F(p) – полином второй или меньшей степени.

Рассмотренные аппроксимации ФНЧ могут быть преобразованы в другие типы фильтров заменой оператора Лапласа в выражениях (5.7) и (5.8) на иную функцию оператора Лапласа. Для полученных в результате этого передаточных функций фильтров, описываемые исходными выражениями (5.7) или (5.8) фильтры, называют ФНЧ-прототипами.

Для перехода от нормированного ФНЧ к ФНЧ с заданной частотой среза ω_с, необходимо выполнить замену переменных:

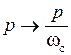. (5.9)

Для перехода от нормированного ФНЧ к ФВЧ с заданной частотой среза ω_с:

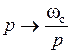. (5.10)

Для перехода от нормированного ФНЧ к ППФ с заданной центральной частотой ω₀:

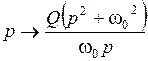, (5.11)

где Q – добротность, которая характеризует избирательность АЧХ фильтра (чем выше добротность Q, тем меньше относительная длина переходной области АЧХ для ФНЧ и ФВЧ; меньше относительная полоса пропускания для ППФ и полоса задерживания для ПЗФ).

Для перехода от нормированного ФНЧ к ПЗФ с заданной центральной частотой ω₀:

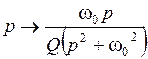. (5.12)

Передаточные функции элементарных звеньев 1-го и 2-го порядка, полученные в результате замен переменных (5.9) – (5.12), примененных к выражениям (5.7) и (5.8), приведены в табл. 5.1.

В передаточных функциях, перечисленных в табл. 5.1, приняты следующие обозначения: k – коэффициент усиления фильтра в полосе пропускания; А, B, С, α, β, γ, ρ – числовые коэффициенты, определяющие форму частотных характеристик соответствующего фильтра; ω_с – частота среза ФНЧ и ФВЧ; ω₀ – центральная частота ППФ и ПЗФ.

Таблица 5.1