Схемы активных фильтров 2-го порядка
Существует достаточно большое количество схем, реализующих передаточные функции фильтров 2-го порядка. Наиболее распространенными являются схема Рауха (схема на основе ОУ с многопетлевой обратной связью), схема Саллен-Ки (схема на основе источника напряжения, управляемого напряжением) и биквадратная схема.
5.4.2.1. Схема Рауха (схема на основе ОУ с многопетлевой
обратной связью)
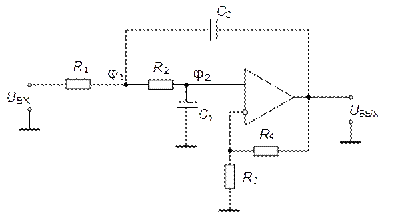
Схема Рауха показана на рис. 5.28.
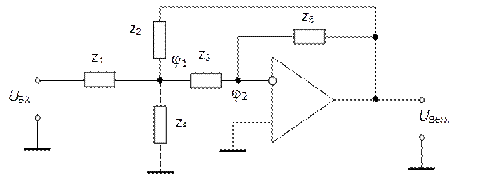
Рис. 5.28. Схема Рауха
Достоинство схемы – минимальное количество элементов
(1 ОУ, 5 пассивных элементов). Недостаток – ограничения по добротности и коэффициенту усиления:
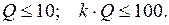
ФНЧ: 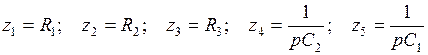 ; (5.16)
; (5.16)
ФВЧ: 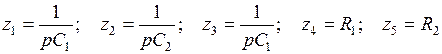 ; (5.17)
; (5.17)
ППФ: 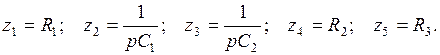 (5.18)
(5.18)
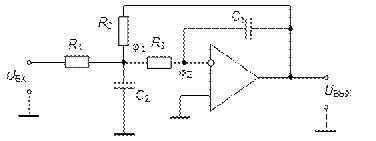 а)
а)
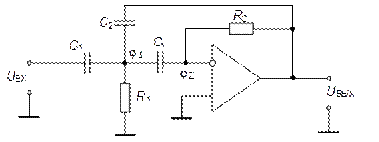 б)
б)
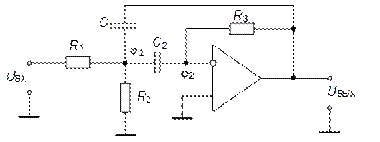 в)
в)
Рис. 5.29. Фильтры 2-го порядка на основе схемы Рауха:
а) – ФНЧ; б) – ФВЧ; в) – ППФ
Для нахождения передаточной функции схемы рис. 5.28 составим систему уравнений для потенциалов φ1 и φ2:
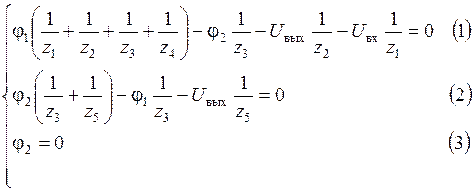
Из (2) с учетом (3): 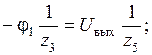
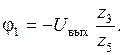 (*)
(*)
Подставляем (3) и (*) в (1):
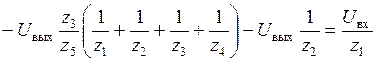 ;
;
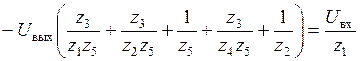 ;
;
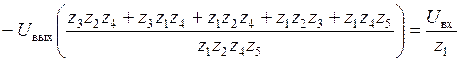 ;
;
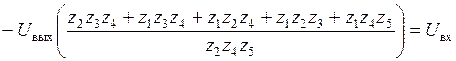 ;
;
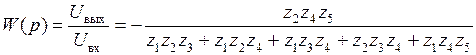 . (5.19)
. (5.19)
После подстановки в передаточную функцию (5.19) схемы Рауха значений (5.16), получается передаточная функция, соответствующая общему виду передаточной функции полиномиального ФНЧ 2-го порядка:
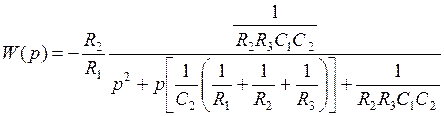 .
.
Коэффициенты передаточной функции ФНЧ:
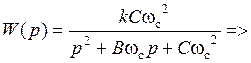
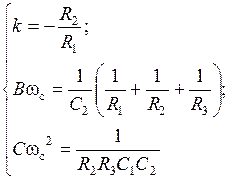
Схемные элементы выбираются из условий:

Регулировки схемы: fc → R3; 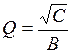 → R1 или R2; k → R2/R1.
→ R1 или R2; k → R2/R1.
После подстановки в передаточную функцию (5.19) схемы Рауха значений (5.17), получается передаточная функция, соответствующая общему виду передаточной функции ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
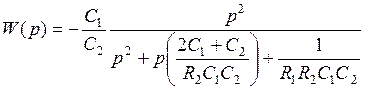 .
.
Коэффициенты передаточной функции ФВЧ:
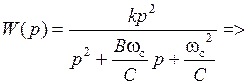
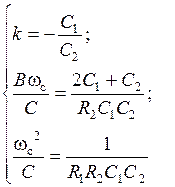
Схемные элементы выбираются из условий:
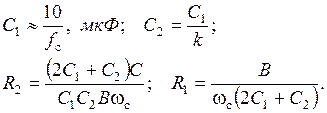
Регулировки схемы: fc → изменение R1 и R2 в равном процентном соотношении; Q → R1 или R2; k → С1/С2.
После подстановки в передаточную функцию (5.19) схемы Рауха значений (5.18), получается передаточная функция, соответствующая общему виду передаточной функции ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
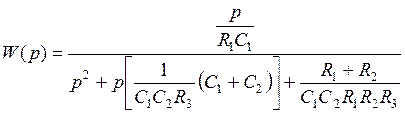 . (5.20)
. (5.20)
Коэффициенты передаточной функции ППФ:
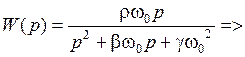
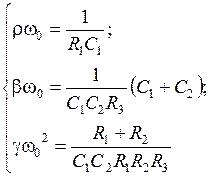
Схемные элементы выбираются из условий:
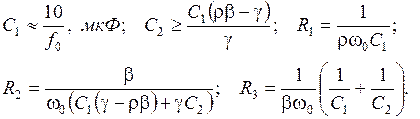
Регулировки схемы: f0 → R2 и R3 (в равном процентном соотношении); 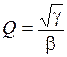 → R2; k → R1.
→ R2; k → R1.
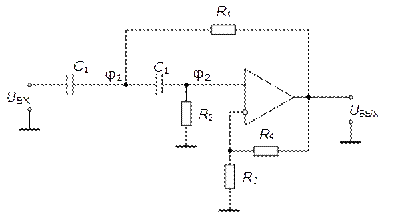
Реализация ПЗФ 2-го порядка на основе схемы Рауха, соответствующая структурной схеме, показанной на рис. 5.25, показана на рис. 5.30.
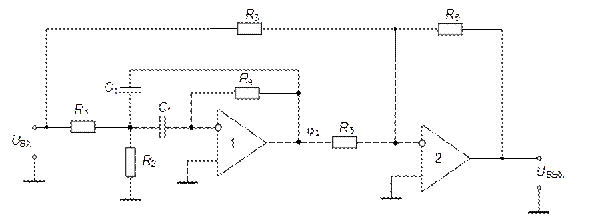
Рис. 5.30. Реализация ПЗФ 2-го порядка на основе схемы Рауха
Для нахождения передаточной функции схемы рис. 5.30, составим систему уравнений для потенциалов φ1 и Uвых:
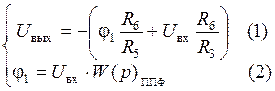
Схема на ОУ1 представляет собой ППФ на основе схемы Рауха, его передаточная функция W(p)ППФ определяется выражением (5.20). С учетом этого уравнение (2) системы запишется в виде:
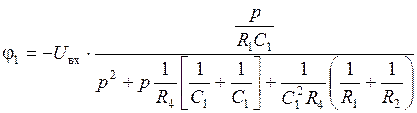 ,
,
подставляем в (1):
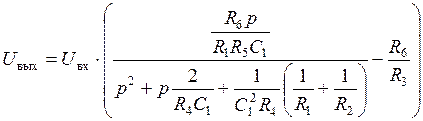 .
.
После упрощения получаем:
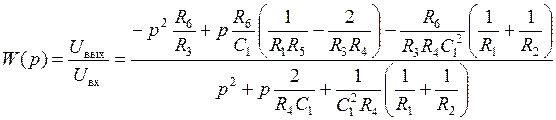 .
.
При соблюдении условия 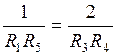 ,
,
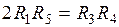 , (*)
, (*)
передаточная функция схемы принимает вид:
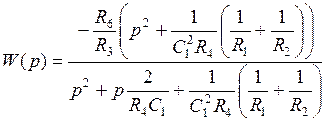 .
.
Из полученного выражения можно определить коэффициенты типовой передаточной функции звена ПЗФ с полиномиальным ФНЧ-прототипом:
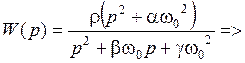
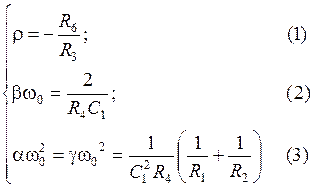
Из (3) видно, что a = g. Следовательно, эта схема применяется исключительно для ПЗФ 2-го порядка или для звеньев ПЗФ 2-го порядка, имеющих ФНЧ-прототип 1-го порядка. Для таких звеньев ПЗФ справедливы соотношения [41]:
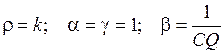 .
.
Задаваясь значениями емкости С1» 10/f0, мкФи сопротивления 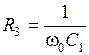 , из (1) – (3), с учетом (*), получим расчетные соотношения для остальных элементов схемы:
, из (1) – (3), с учетом (*), получим расчетные соотношения для остальных элементов схемы:
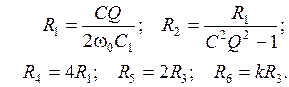
Регулировки схемы: f0 → R2 (без изменения добротности);
k → R6.
5.4.2.2. Схема Саллен-Ки (схема на основе источника
напряжения, управляемого напряжением)
Схема Саллен-Ки показана на рис. 5.31.
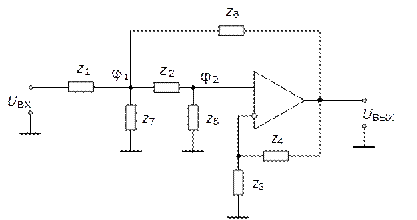
Рис. 5.31. Схема Саллен-Ки
Достоинство схемы – высокое входное сопротивление.
Недостаток – ограничения по добротности и коэффициенту усиления:
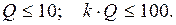
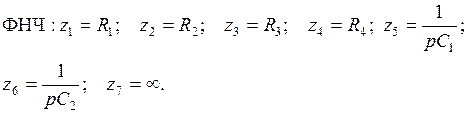 (5.21)
(5.21)
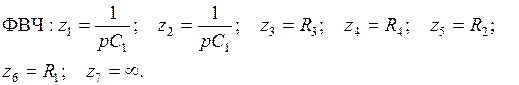 (5.22)
(5.22)
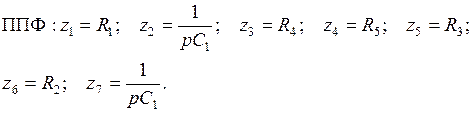 (5.23)
(5.23)
 а)
а)
 б)
б)
 в)
в)
Рис. 5.32. Фильтры 2-го порядка на основе схемы Саллен-Ки:
а) – ФНЧ; б) – ФВЧ; в) – ППФ
Для нахождения передаточной функции схемы Саллен-Ки (рис. 5.31) составим систему уравнений для потенциалов φ1 и φ2:
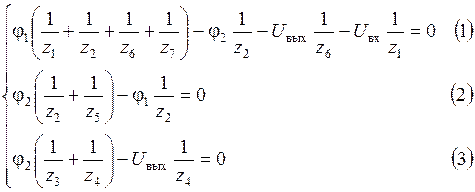
Из (2): 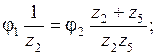
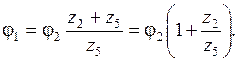
Из (3): 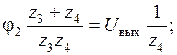
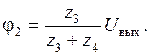
Подставляем в (1):
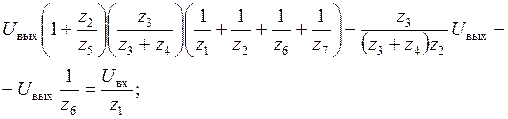
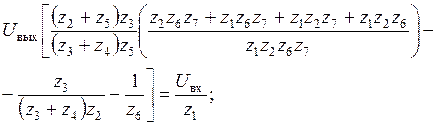
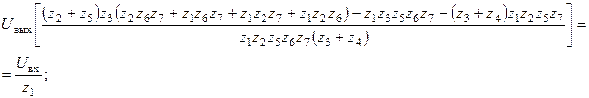
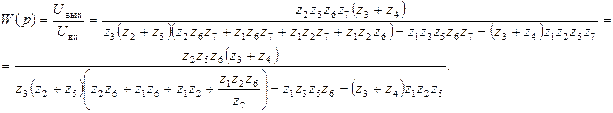
|
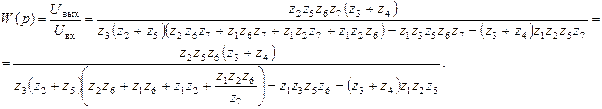
После подстановки в передаточную функцию (5.24) схемы Саллен-Ки значений (5.21), получается передаточная функция, соответствующая общему виду передаточной функции ФНЧ 2-го порядка:
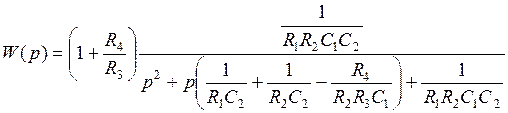 .
.
Коэффициенты передаточной функции ФHЧ:
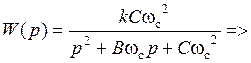
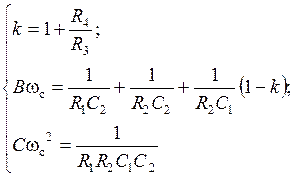
Учитывая условие симметрирования ОУ: 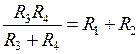 , получаем расчетные соотношения для элементов схемы:
, получаем расчетные соотношения для элементов схемы:
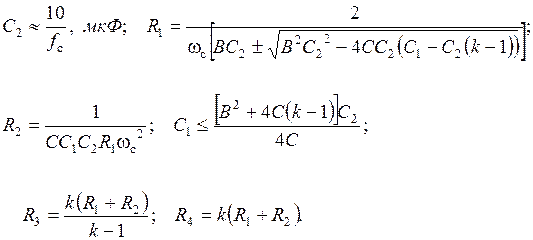
Регулировки схемы: fc → R1 и R2 (в равном процентном соотношении); 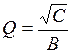 → R1 или R2; k → R4/R3.
→ R1 или R2; k → R4/R3.
После подстановки в передаточную функцию (5.24) схемы Саллен-Ки значений (5.22), получается передаточная функция, соответствующая общему виду передаточной функции ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
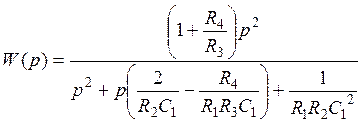 .
.
Коэффициенты передаточной функции ФВЧ:
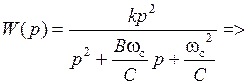
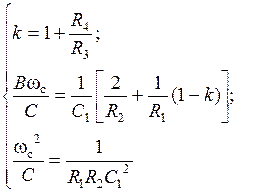
Учитывая условие симметрирования ОУ: 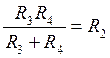 , получаем расчетные соотношения для элементов схемы:
, получаем расчетные соотношения для элементов схемы:
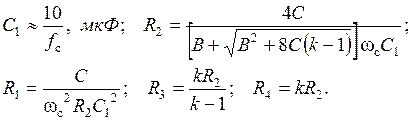
Регулировки схемы: fc → R1 и R2 (в равном процентном соотношении); 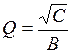 → R1 или R2; k → R4/R3.
→ R1 или R2; k → R4/R3.
После подстановки в передаточную функцию (5.24) схемы Саллен-Ки значений (5.23), получается передаточная функция, соответствующая общему виду передаточной функции ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
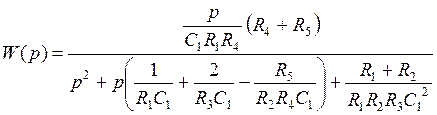 .
.
Принимая обозначение 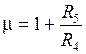 , запишем коэффициенты передаточной функции ППФ:
, запишем коэффициенты передаточной функции ППФ:
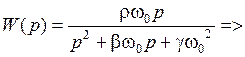
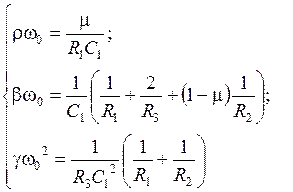
Для удобства примем μ=2.Учитывая условие симметрирования, дополнение к системе имеет вид:
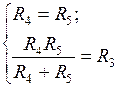
Схемные элементы выбираются из условий:
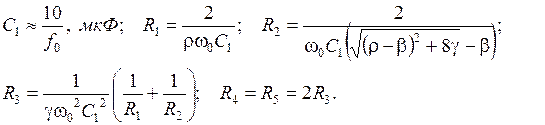
Регулировки схемы: f0 → R3; 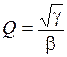 → R2 или R3; k → R1.
→ R2 или R3; k → R1.
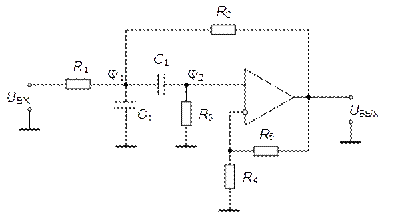
Реализация ПЗФ 2-го порядка на основе схемы Саллен-Ки, требует использования схемы иной топологии, показанной на рис. 5.33.
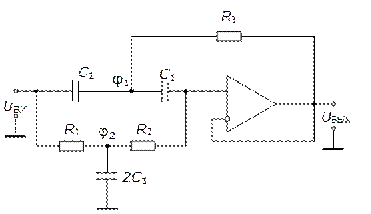
Рис. 5.33. Реализация ПЗФ 2-го порядка на основе схемы Саллен-Ки
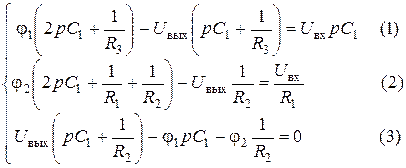
Из (3): 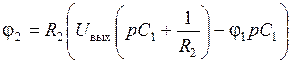 , подставляем в (2):
, подставляем в (2):
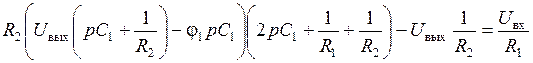 (2’).
(2’).
Из (1):
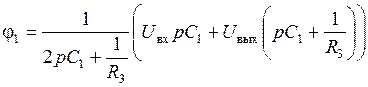 . (1’)
. (1’)
Подставляем (1’) в (2’) с учетом равенства:
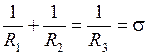 . (*)
. (*)
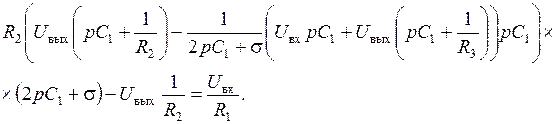
После упрощений получаем:
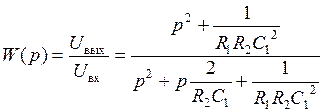 .
.
Из полученного выражения можно определить коэффициенты типовой передаточной функции звена ПЗФ 2-го порядка с полиномиальным ФНЧ-прототипом:
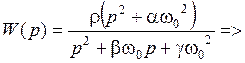
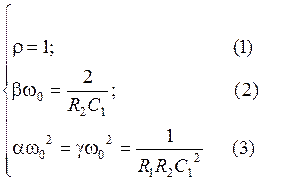
Из (3) видно, что a = g, а из (1), что коэффициент усиления равен 1. Следовательно, эта схема предназначена только для реализации ПЗФ 2-го порядка или звеньев ПЗФ 2-го порядка, имеющих ФНЧ-прототип 1-го порядка.
С учетом того, что для звена ПЗФ 2-го порядка, имеющего ФНЧ-прототип 1-го порядка, 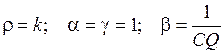 , схемные элементы выбираются из условий:
, схемные элементы выбираются из условий:
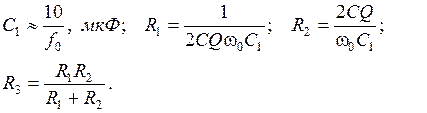
Регулировки схемы: R1 → Q; R2 → f0.
Биквадратная схема
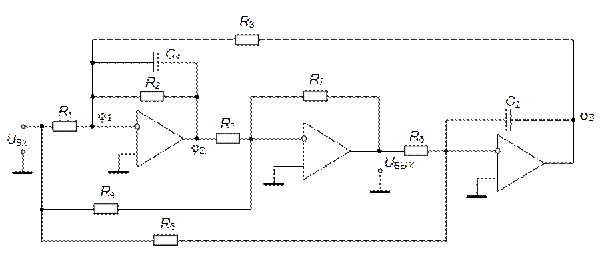
Биквадратная схема показана на рис. 5.34.
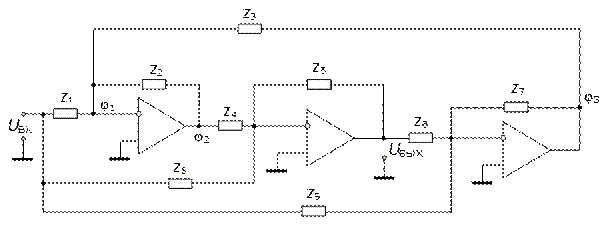 Рис. 5.34. Биквадратная схема
Рис. 5.34. Биквадратная схема
Достоинства схемы:
1) высокая возможная добротность:
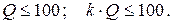
2) возможность построения звеньев, реализующих как полиномиальные (Баттерворта, Чебышева, Бесселя), так и неполиномиальные аппроксимации ЧХ (инверсный Чебышева, Кауэра).
Недостатки:
1) высокие аппаратные затраты;
2) сложность настройки с учетом обеспечения точных соотношений номиналов резисторов.
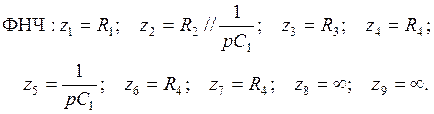 (5.25)
(5.25)
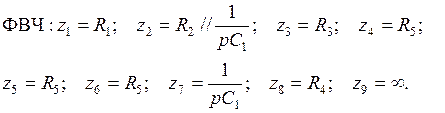 (5.26)
(5.26)
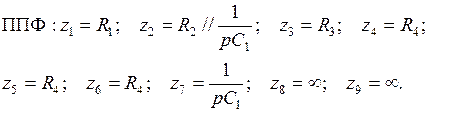 (5.27)
(5.27)
Неполиномиальный ФНЧ (инверсный Чебышева и Кауэра);
ФВЧ, ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом:
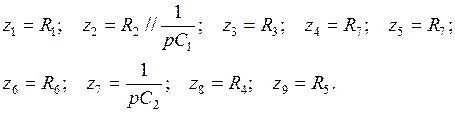 (5.28)
(5.28)
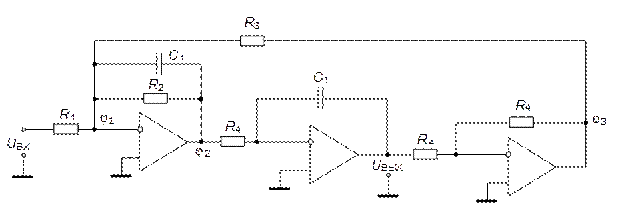 а)
а)
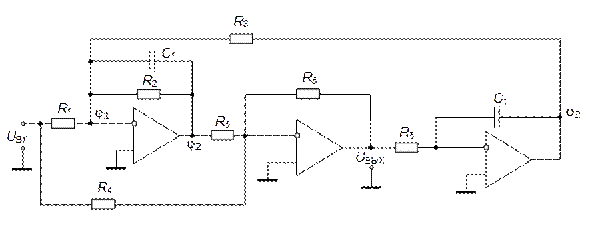 б)
б)
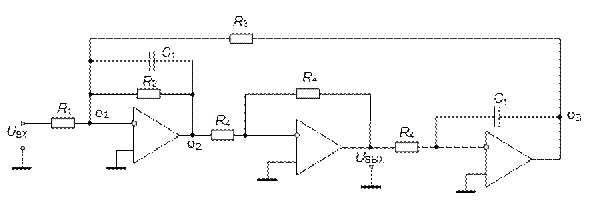 в)
в)
 г)
г)
Рис. 5.35. Фильтры 2-го порядка на основе биквадратной схемы: а) – ФНЧ;
б) – ФВЧ; в) – ППФ; г) – неполиномиальный ФНЧ; ФВЧ, ППФ и ПЗФ
с неполиномиальным ФНЧ-прототипом
Составим систему уравнений для потенциалов φ1, φ2, и φ3 схемы рис. 5.34:
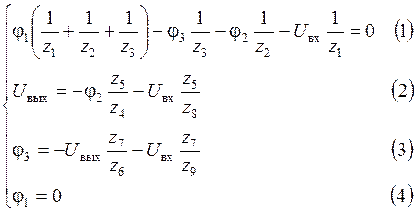
Из (2): 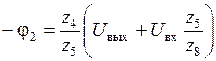 . (*)
. (*)
Подставляем (*), (3) и (4) в (1):
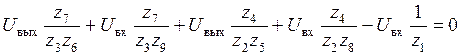 ;
;
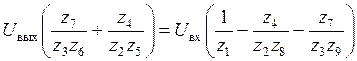 ;
;
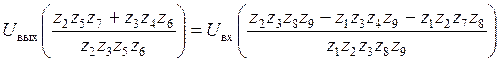 ;
;
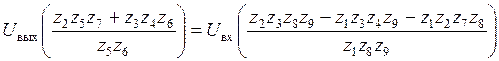 ;
;
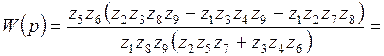
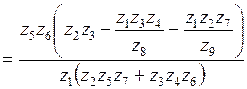 . (5.29)
. (5.29)
После подстановки в передаточную функцию (5.29) биквадратной схемы значений (5.25), получается передаточная функция, соответствующая общему виду передаточной функции полиномиального ФНЧ 2-го порядка:
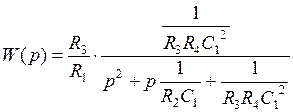 .
.
Коэффициенты передаточной функции ФHЧ:
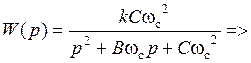
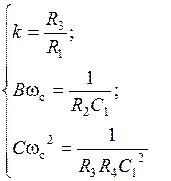
Схемные элементы выбираются из условий:
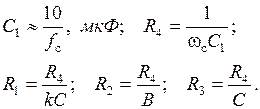
Регулировки схемы: fc → R3; 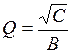 → R2; k → R1.
→ R2; k → R1.
После подстановки в передаточную функцию (5.29) биквадратной схемы значений (5.26), при соблюдении в схеме рис. 5.35, б условия:
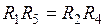 (*),
(*),
получается передаточная функция, соответствующая общему виду передаточной функции ФВЧ 2-го порядка с полиномиальным ФНЧ-прототипом:
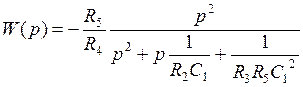 .
.
Коэффициенты передаточной функции ФВЧ:
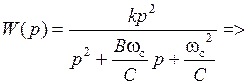
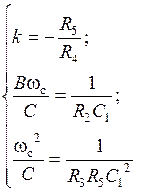
Схемные элементы выбираются из условий:
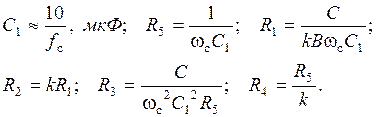
Регулировки схемы: fc → R3; 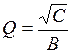 → R2; k → R1.
→ R2; k → R1.
После подстановки в передаточную функцию (5.29) значений (5.27), получается передаточная функция, соответствующая общему виду передаточной функции ППФ 2-го порядка с полиномиальным ФНЧ-прототипом:
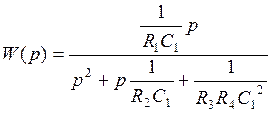 .
.
Коэффициенты передаточной функции ППФ:
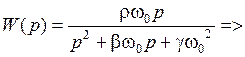
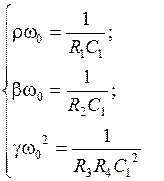
Схемные элементы выбираются из условий:
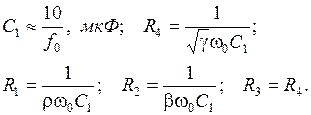
Регулировки схемы: f0 → R3; 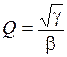 → R2; k → R1.
→ R2; k → R1.
После подстановки в передаточную функцию (5.29) значений (5.28), при соблюдении в схеме рис. 5.35, г условия:
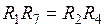 (*),
(*),
получается передаточная функция, соответствующая общему виду передаточной функции неполиномиального звена 2-го порядка:
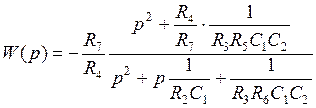 .
.
Коэффициенты передаточной функции неполиномиального ФHЧ:
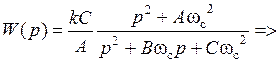
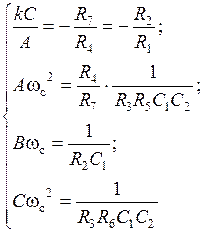
Емкость C1 выбирается из условия:
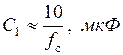 .
.
При реализации фильтров, имеющих невысокую добротность, емкость C2 может быть выбрана равной емкости С1, но в общем случае они могут быть не равны между собой. Значение R7 выбирается из условия:
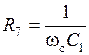 .
.
Остальные схемные элементы выбираются из условий:
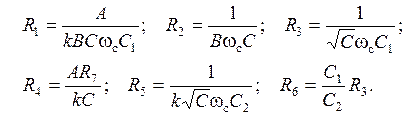
Регулировки схемы: максимальное подавление в полосе задерживания → R4; fc → R3; 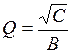 → R2; k → R1 или R5.
→ R2; k → R1 или R5.
Коэффициенты передаточной функции ФВЧ с неполиномиальным ФНЧ-прототипом:
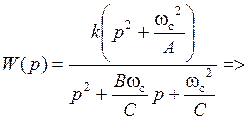
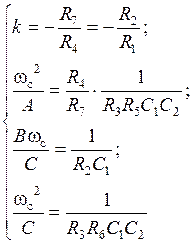
Емкость C1 выбирается из условия:
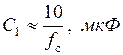 .
.
При реализации фильтров, имеющих невысокую добротность, емкость C2 может быть выбрана равной емкости С1, но в общем случае они могут быть не равны между собой. Значение R7 выбирается из условия:
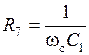 .
.
Остальные схемные элементы выбираются из условий:
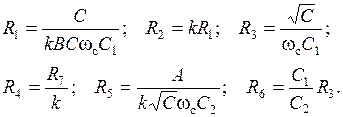
Регулировки схемы: максимальное подавление в полосе задерживания → R4; fc → R3; 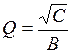 → R2; k → R1.
→ R2; k → R1.
Коэффициенты передаточной функции ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом:
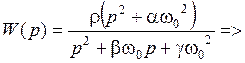
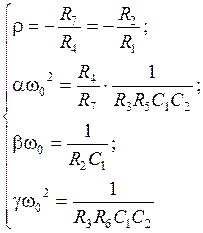
Емкость C1 выбирается из условия:
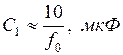 .
.
При реализации фильтров, имеющих невысокую добротность, емкость C2 может быть выбрана равной емкости С1, но в общем случае они могут быть не равны между собой. Значение R7 выбирается из условия:
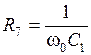 .
.
Остальные схемные элементы выбираются из условий:
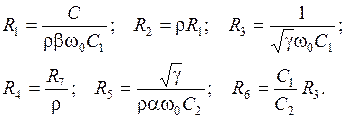
Если добротность Q и (или) коэффициент усиления k имеют значения более 10, то C2 и R7 должны выбираться таким образом, чтобы сохранился небольшой разброс значений сопротивлений схемы.
Регулировки схемы: максимальное подавление в полосе задерживания → R4; f0 → R3; 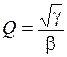 → R2; r → R1 или R5.
→ R2; r → R1 или R5.
Реализованные на биквадратной схеме неполиномиальный ФНЧ (инверсный Чебышева и Кауэра); ФВЧ, ППФ и ПЗФ с неполиномиальным ФНЧ-прототипом имеют одну и ту же схемную реализацию, и один и тот же вид передаточной функции. Разница в их частотных характеристиках обусловлена различными соотношениями 4-х коэффициентов, входящих в передаточную функцию.
Дата добавления: 2015-11-26; просмотров: 12305;
