Примеры построения чертежей деталей, усеченных проецирующими плоскостями

Иногда на практике возникает необходимость в построении фигуры сечения не на проекциях детали, а отдельно на чертеже, на- пример с целью определения истинной величины этой фигуры. Если при этом секущая плоскость наклонена к плоскостям проекций, сечение называют наклонным

Пример наклонного сечения детали дан на рис 6.11 Как видно из чертежа, фигура сечения детали фронтально-проецирующей пло- скостью состоит из прямоугольника (результат пересечения наруж- ной поверхности детали — многогранника) и эллипса (результат пересечения плоскостью цилиндрического отверстия). Кроме того, в плоскость сечения попали прямоугольный вырез, идущий вдоль основания детали, два цилиндрических отверстия, из них одно сквозное, и вырез в верхней части детали. Цилиндрические отверстия изображаются в форме прямоугольников, так как секущая плоскость направлена вдоль образующих этих поверхностей.

Истинная величина фигуры сечения определена способом замены плоскостей проекций.Ось проекций новой системы на чертеже не по

казана. Поскольку полученная фигура сечения симметрична, в подстроении ее использована ось симметрии.Начертеже эту ось лучше располагать параллельно следу секущей плоскости. Тогда все размеры, выражающие длину фигуры сечения (I) и ее частей, могут быть непосредственно с помощью линий проекционной связи перенесены с фронтальной проекции на указанную ось. Размеры, относящиеся к ширине фигуры сечения (/; и др.), взяты с горизонтальной проекции.

Величина большой оси эллипса, как проекции линии сечения цилиндра наклонной плоскостью, определена по фронтальной проекции. Малая ось равна диаметру цилиндрического отверстия.

Фигуру сечения детали можно размещать и не в проекционной связи с фронтальной проекцией, в том числе и с ее поворотом.

Рис 6.11

МЕТРИЧЕСКИЕ ЗАДАЧИ

Метрическими называются задачи, в которых приходится определять значения измеряемых величин - измерять величину угла между' двумя прямыми и расстояние между двумя точками.

К метрическим относятся также задачи на построение угла и отрезка с наперед заданным соответственно градусной и линейной величины.

В основе алгоритма решения любой метрической задачи лежит свойство плоской фигуры, параллельной плоскости проекций: она (фигура) проецируется на эту плоскость в конгруентную фигуру;

ф½½аÞФа@Ф.

В задачах на построение проекций угла, равного 90°, используется теорема о частном случае проецирования прямого угла: прямой угол проецируется ортогонально без искажения, если одна из его сторон параллельна плоскости проекции, а вторая сторона не перпендикулярна к этой плоскости:

([АВ]^[ВС])Ç([АВ]½½a,[ВС]^a)Þ[А^aВ^a]^[В^aС^a]

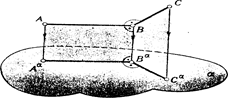
Рис 7.1

При определении расстояния между двумя точками или построении отрезка заданной длины можно использоватькак методы преобразования ортогональных проекций, так и пользоваться построением прямоугольного треугольника.

Отметим ряд свойств ортогональных проекцийплоскихуглов (доказательства рассмотреть самостоятельно).

2. Если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол:

а) проекция острого угла будет меньше проецируемого угла;

б) прямой угол проецируется без искажения;

в) проекция тупого угла больше проецируемого угла,

3.Если обе стороны любого угла параллельны плоскости проекции, то на эту плоскость он проецируется без искажения.

4.Проекции острого и тупого углов могут проецироваться на плоскость без искажения не только при условии параллельности сторон угла плоскости проекции.

5. Если стороны угла параллельны плоскости проекции или одинаково наклонены к ней, то деление пополам проекции угла соответствует его делению пополам в пространстве.

Если проекция некоторого угла, у которогоодна сторона, параллельная плоскости проекции, равна прямому углу, то и проецируемый угол также