Пересечение конуса с плоскостью

В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые вершину конуса, в его сечении получается пара прямых - образующие конуса ( рис 6.6, а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис 6.6, б).

Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться парабола (рис.6.6. в), гипербола (рис.6.6, г) или эллипс (рис.6.6.д,е).

Если углы a (угол наклона образующей конуса к его оси) и b (угол наклона секущей плоскости к оси конуса) равны, т.е. секущая плоскость параллельна одной из образующих конуса, в сечении получается парабола (рис^.6.6, в). В этом случае секущая плоскость a(av) пересекает все образующие, кроме одной, которой она параллельна.

Если секущая плоскость а (a v), направленная под углом к оси вращения конуса, пересечет его так, что угол b будет меньше угла a, то в сечении получится гипербола (рис.6.6.г). В этом случае секущая плоскость параллельна двум образующим конуса.

Эллипс получается в том случае, когда угол b между секущей плоскостью a (a_n) и осью вращения больше, чем угол a между осью вращения и образующей конуса (рис.6.6. д, е), т.е. когда плоскость пересекает все образующие конуса.

На рис.6.7 дано построение проекций линии сечения конуса фронтально - проецирующей плоскостью a, когда в сечении получается эллипс. На фронтальной плоскости проекций V фигура сечения - эллипс - изобразится в виде прямой А²В², совпадающей с фронтальной проекцией a_n секущей плоскости. Эта прямая будет большой осью эллипса. Малая ось эллипса перпендикулярна большой и проходит через ее середину. Отрезок А²В²делят пополам и получают фронтальную проекцию малой оси в виде точки C²D". Для нахождения горизонтальной проекции малой оси через нее проводят параллель, которая проецируется на горизонтальную

плоскость проекции окружностью радиусаО¢Т¢. Точки 1 и 1^- сечения принадлежат профильным очерковым образующим конуса.Ониотделяют видимую в профильной проекции часть l²¢-C²¢-A "'-D"'-1^-'^//

сечения от невидимой 1²¢-В²¢ -1^-///.

Натуральная величина сечения AoBoCoDo построена способом замены плоскостей проекций на плоскости Т, перпендикулярной плоскости V. Большая ось эллипса - отрезок АоВо @ А₂В₂, малая - отрезок CoDo @ d. Наряду с построением эллипса по точкам возможно построение его по большой и малой осям.

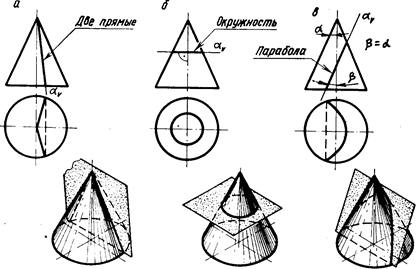
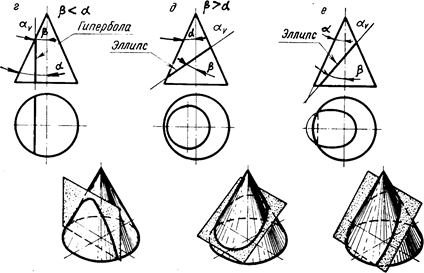
Рис 6.6

81

Рис 6.7