Пересечение цилиндра с плоскостью

При пересечении цилиндра плоскостью фигура сечения будет зависеть от угла наклона плоскости по отношению к оси вращения.

Если секущая плоскость параллельна оси вращения (рис 6.4 а ), в сечении цилиндра получится прямоугольник. Если плоскость перпендикулярна оси вращения (рис 6.4 , б), в сечении получится окружность.

Когда секущая плоскость расположена под углом к оси вращения цилиндра, в сечении получается эллипс (рис 6.4 в) или его часть ( рис 6.4', г).

Рис 6.4

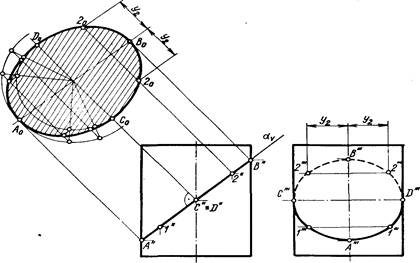
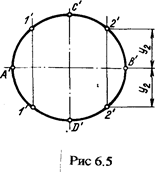
На рис 6.5 показано построение проекций линиисечения цилиндра фронтально - проецирующей плоскостью a (a_v).

Линией пересечения является эллипс. Большая ось эллипса - АВ = А' 'В'^/, малая ось CD = С¢D¢ - диаметр цилиндра.

Ось цилиндра и вся цилиндрическая поверхность перпендикулярны плоскости Н. Следовательно, все точки цилиндрической поверхности, в том числе и линия пересечения ее с плоскостью а(а ) проецируется на плоскость Н в окружность, на ней отмечают горизонтальные проекции точек А¢,1¢, С¢, 2¢, В', D', 2', 1' эллипса, расположив их равномерно по окружности. В проекционной связи строят фронтальные проекции А², \", С², В², 2^//, В² на фронтальном следе a_v секущей плоскости.

Профильные проекции точек строят по их горизонтальной и фронтальной проекциям на линиях связи. Профильная проекция линии пересечения цилиндра с секущей плоскостью - эллипс, большая ось C²¢D²¢ которого в данном случае равна диаметру цилиндра , а малая ось А²¢В²¢ - профильная проекция отрезка АВ. Натуральный вид сечения построен способом замены плоскостей проекций на плоскости Т, перпендикулярной плоскости V. Большая ось эллипса - отрезок АоВо @ A₂B₂, малая - отрезок CoDo @ d. Эллипс может быть построен по его большой и малой осям.