Способ вспомогательных секущих плоскостей

На рис 5.13 показано, что две криволинейные поверхности А и В пересекаются третьей секущей вспомогательной плоскостьюQ, Находят линии пересечения KL и MN вспомогательной поверхности с каждой из заданных. Точка Т пересечения построенных линий KL и MN принадлежат линии пересечения заданных поверхностей А и В.

Повторяя такие построения многократно с помощью других вспомогательных поверхностей, находят необходимое число общих точек двух поверхностей для построения линии их пересечения.

Сформулируем общее правило построения линии пересечения поверхностей:

выбирают вид вспомогательных поверхностей;

строят линии пересечения вспомогательных поверхностей с заданными поверхностями;

находят точки пересечения построенных линий и соединяютих между собой.

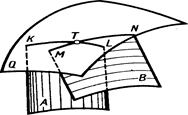
Рис 5.13

Вспомогательные секущие плоскости выбираем таким образом, чтобы в пересечении с заданными поверхностями получались геометрически простые линии (прямые или окружности).

Пример. Построить линию пересечения конуса вращения и сферы (рис 5.14 ). Алгоритм решения;

1) К,СфÇТn(Qn)

2) KÇTv=n;

3) СфÇa=m;

4) mÇn= 6-5

Выбираем вспомогательные секущие плоскости.Чаще всего, в качестве вспомогательных секущих плоскостей выбирают проецирующие плоскости, в частности, плоскости уровня. При этом необходимо учитывать линии пересечения, получаемые на поверхности, в результате пресечения поверхности плоскостью. Так конус является наиболее сложной поверхностью по числу получаемых на нем линий.

Только плоскости, проходящие через вершину конуса или перпендикулярные оси конуса, пересекают его соответственно по прямой линии и окружности (геометрически простейшие линии). Плоскость, проходящая параллельно одной образующей пересекает его по параболе, плоскость параллельная оси конуса пересекает его

по гиперболе, а плоскость, пересекающая все образующие и наклонные к оси конуса, пересекает его по эллипсу.

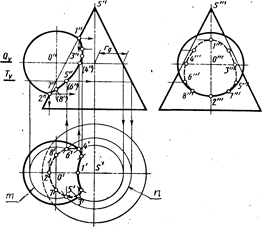
Рис 5.14

На сфере, при пересечеиии ее плоскостью, всегда получается окружность, а если пересекать ее плоскостью уровня, то эта окружность проецируется на плоскости проекции соответственно в прямую линию и окружность.

Итак, в качестве вспомогательных плоскостей выбираем горизонтальные плоскости уровня, которые пересекают и конус, и сферу по окружностям (простейшие линии).

Построение начинают обычно с отыскания проекций характерных точек. Проекции 1¢¢ высшей и 2¢¢ низшей точек являются точками пересечения фронтальных проекций очерков, так как центр сферы и ось конуса лежат в плоскости, параллельной плоскости V. их горизонтальные 1¢, 2¢ и профильные 1''',2"¢ про-

екции находят в проекционной связи. Проекции 3",3',3"' и 4^//,4^/,4^/'', лежащие на экваторе

сферы, находят с помощью горизонтальной плоскости Q(Qv), проходящей через центр сферы 0(0¢¢ ). Она пересекает сферу по экватору и конус по окружности радиуса r_q, в пересечении горизонтальных проекций которых и находят горизонтальные проекции 3¢ и 4¢ точек искомой линии пересечения. Горизонтальные проекции 3¢ и 4¢ этих точек являются границами видимости участков линии пересечения на этой проекции. Проекции промежуточных точек, например 5¢¢,5',5¢¢¢ и 6¢¢,6¢,6¢¢, находят с помощью вспомогательной горизонтальной плоскости Т (Тv). Их построение ясно из чертежа. Аналогично построены другие точки. Профильные проекции точек линии пересечения строят по их фронтальной и горизонтальной проекциям, точки с проекциями 7¢¢,7¢,7¢¢¢ и 8¢¢,8¢,8"¢ являются границами видимости участков профильной проекции линии пересечения. Ниже проекций 7¢¢¢ и 8"' профильная проекция линии пересечения видима.

5.7.Способ вспомогательных секущих сфер с постоянным
центром

Известно, что если центр сферы находится на оси какой- нибудь поверхности вращения, то сфера соосна с поверхностью вращения и в их пересечении получаются окружности AB,CD, EF, КL(,рис5.15 ).

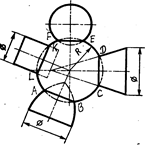
Рис 5.15.

Это свойство сферы с центром на оси какой-либо поверхности вращения и положено в основу способа концентрических сфер, который применяют при следующих условиях:

1.0бе пересекающиеся поверхности- поверхности вращения.

2. Оси поверхностей пересекаются; точку пересечения принимают за центр вспомогательных, (концентрических) сфер.

3.Плоскость, образованная осями поверхностей (плоскость симметрии), должна быть, параллельна плоскости проекции. Еслиэто условие не соблюдается, то чтобы его достигнуть, прибегают к способам преобразования чертежа.

Пример. Определить линию пересечения двух конических поверхностей с пересекающимися осями (рис 5.16).

Рис.5.16

Построение начинаем с определения характерных точек А, В, С D, которые лежат во фронтальной плоскости, проходящей через плоскость симметрии поверхностей. Их фронтальные проекции А",В ,С ,D определяются пересечением главных меридианов. Далее определяем сферы R min и R max. Сфера R min определяется двумя способами:

1.Если образующие пересекающихся поверхностей прямые линии, то из центра 0¢¢ проводим перпендикуляры к образующим заданных поверхностей. Наибольший из этих перпендикуляров будет являться R min.

2. Если образующая хотя бы одной поверхности кривая линия, то R min находится подбором, т.е. сфера R min должна быть, вписана в одну поверхность и описана вокруг другой.

Сфера R max - это расстояние от центра 0¢' до наиболее удаленной от него точки линии пересечения. В нашем случае это 0"В¢¢.

Величина радиуса вспомогательных сфер для определения линии пересечения находим в пределах от R min = (О¢'М¢¢) до R max = (О¢¢ В¢¢). Точка М¢¢ определяется как точка касания окружности, проведенной к главному меридиану m¢¢₂ из центра О¢¢. Для определения линии L₂-Rmax=½О"С"½, R min =½О¢¢М¢¢½. Для определения точек N¢¢₁ и N¢¢₂, принадлежащих линии 1₂ находим окружность (на фронтальной плоскости - прямая), по которой пересекаются конус a¢¢ и сфера R min, и находим окружность (на фронтальной плоскости - прямая), по которой пересекаются конус b¢¢ и сфера R min . на пресечении этих линий находим точки N¢¢₁и N¢¢_2.

Построив несколько сфер с центром в точке О¢¢, в промежутке,

между R min и R max находим точки, принадлежащие линии пересечения

Вторую проекцию линии пересечения строят исходя из условия принадлежности точек этой линии той или другой поверхности.

Недостаток метода сфер

1) При построении должна соблюдаться графическая точность.

2) Линия пересечения строится на одной плоскости проекций.