Точка и линия на поверхности
 Выше было сказано, что поверхность считается заданной, если по одной проекции точки на поверхности можно построить ее вторую проекцию. Так же ранее было дано определение принадлежности точки плоскости (частный случай поверхности). Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности. Причем линии, проведенные через точку на данной поверхности должны быть геометрически простейшими (прямыми или окружностями). Положение точки на поверхности вращения определяют с помощью окружности, проходящей через эту точку на поверхности вращения. В случае линейчатых поверхностей для этой цели возможно применение и прямолинейных образующих.
Выше было сказано, что поверхность считается заданной, если по одной проекции точки на поверхности можно построить ее вторую проекцию. Так же ранее было дано определение принадлежности точки плоскости (частный случай поверхности). Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности. Причем линии, проведенные через точку на данной поверхности должны быть геометрически простейшими (прямыми или окружностями). Положение точки на поверхности вращения определяют с помощью окружности, проходящей через эту точку на поверхности вращения. В случае линейчатых поверхностей для этой цели возможно применение и прямолинейных образующих.
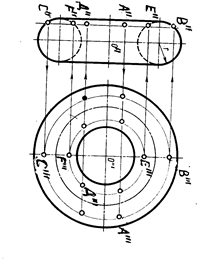
На рис 5.9 показано построение точки К принадлежащей поверхности тора. Следует отметить, построение выполнено для видимых горизонтальной проекции К и фронтальной проекции К .Для построения К по заданной проекции К", через К" проводим параллель, которая на фронтальную плоскость проецируется в прямую линию, а на горизонтальную плоскость в окружность, на которой находим К'.
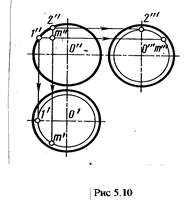
На рис 5.10 показано построение по заданной фрактальной
проекции m" точки на поверхности
Рис 5.9
сферы ее горизонтальной m¢ и
 61
61
профильной m'" проекцией. Проекция m построена с помощью
окружности - параллели, проходящей через проекцию m . Ее радиус - O'-l' . Проекция т" построена с помощью окружности, плоскость которой параллельна профильной плоскости проекций, проходящей через проекцию m¢'. Ее радиус - О -m".
Дата добавления: 2016-01-11; просмотров: 2141;
