Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости.
Поэтому построение плоскости a, перпендикулярной к плоскостиb,можно осуществить двумя путями;
1. Проводим прямую m, перпендикулярную к плоскости b (или a), затем прямую m заключаем в плоскость a (или b).
2. Проводим прямую n, принадлежащую или параллельную плоскости b (или a), затем строим плоскость a (илиb), перпендикулярно к прямой n.
 Так как через прямую m можно провести множество плоскостей (первый путь решения), то задача имеет множество решений. То же самое происходит и при решении по второму пути ( в плоскости или параллельно ей можно провести множество прямых n). Чтобы конкретизировать задачу, необходимо указать дополнительные условия.
Так как через прямую m можно провести множество плоскостей (первый путь решения), то задача имеет множество решений. То же самое происходит и при решении по второму пути ( в плоскости или параллельно ей можно провести множество прямых n). Чтобы конкретизировать задачу, необходимо указать дополнительные условия.
Пример 1. Чрез данную прямую а провести плоскость a, перпендикулярную к плоскостиb, заданной параллельными прямыми 1 и f (рис.7.7.).
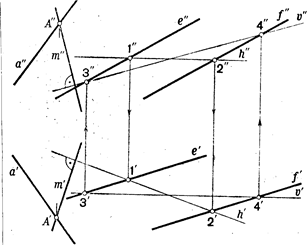
Рис 7.7
1. Определяем направление проекций перпендикуляра к плоскости a. для этого находим горизонтальную проекцию горизонтали h' и фронтальную проекцию фронтали u²,
2. Из проекции произвольной точки Аеа проводим проекции перпендикуляра m'^h' и m²^u². Плоскость a^b, т.к m^b
Пример 2.Через данную точку А провести горизонтально проецирующую плоскость b, перпендикулярную к плоскости a, заданной следами (рис.7.8)
Искомая плоскость рдолжна проходить перпендикулярно к прямой, принадлежащей плоскости a В связи с тем, что плоскость b должна быть горизонтально проецирующей, то прямая, перпендикулярная к ней , должна быть параллельна плоскости H, т.е. являться горизонталью плоскости а или (что тоже самое) горизонтальным следом этой плоскости - aн. Поэтому через горизонтальную проекцию точки А¢ проводим горизонтальный след bн^aн, фронтальный след bv^оси X.
7.3. Определение действительной величины угля между прямой и плоскостью. Между двумя плоскостями
 Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на данную плоскость (прямая не перпендикулярна плоскости).
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на данную плоскость (прямая не перпендикулярна плоскости).
Пространственная геометрическая модель, иллюстрирующаяэто определение, показана на рис 7.9 .
План решения задачи может быть, записан:
1 .Из произвольной точки АÎa опускаем перпендикуляр на плоскость;
2. Определяем точку встречи этого перпендикуляра с плоскостью a(точка Аa ортогональная проекция точки А на плоскость a);
3.Находим точку пересечения прямой a с плоскостью а (точка Аa- след прямой а на плоскости a);
4.Проводим (А°Аa)- проекдию прямой а на плоскость a;
 5.Определяем действительную величину ÐААaАa,т.е.Ðj0. Решение этой задачи может быть значительно упрощено, если определять не Ðj0между прямой и плоскостью, а дополнительный до 90° Ðg° В этом случае отпадает необходимость в определении точки Аa и
5.Определяем действительную величину ÐААaАa,т.е.Ðj0. Решение этой задачи может быть значительно упрощено, если определять не Ðj0между прямой и плоскостью, а дополнительный до 90° Ðg° В этом случае отпадает необходимость в определении точки Аa и
проекции аaЗная величину у0 , вычисляем— j0=90-g0.
Дата добавления: 2016-01-11; просмотров: 1065;
