Задачи принятия решений

Исследование операций включает в себя целый ряд научных дисциплин, отличающихся целями и методами принимаемых решений:

·

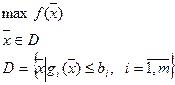
где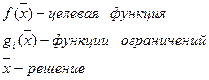

Задача (1–2) относится к классу экстремальных задач. Если область допустимых решений D совпадает с пространством вещественных чисел Rⁿ, то есть отсутствуют ограничения (2),то данная экстремальная задача является классической задачей оптимизации.

· Линейное программирование. Задача линейного программирования – это задача математического программирования (1–2), в которой целевая функция и функции ограничений линейные. Для таких задач разработаны точные методы решений.

· Транспортные задачи – задачи линейного программирования специального вида, имеющие более эффективные методы решений.

· Задачи о назначениях – задачи о распределении работы между исполнителями с целью достижения максимальной эффективности.

· Задачи нелинейного программирования – задачи математического программирования, в которых хотя бы одна из функций нелинейна. В общем случае эти задачи не имеют точных аналитических методов решений. Основные методы их решения – приближенные.

· Задачи выпуклого программирования – задачи нелинейного программирования, имеющие вогнутую (Ç) функцию цели и выпуклую (È) область допустимых значений. Это гарантирует одноэкстремальность задачи и позволяет сформулировать признак оптимальности решения.

· Задачи квадратичного программирования – задачи выпуклого программирования, имеющие квадратичную целевую функцию с линейными ограничениями.

· Задачи дискретного программирования – задачи математического программирования, имеющие дискретную область допустимых решений (в частности, конечное или счетное множество решений).

· Задачи динамического программирования – задачи, в которых применяются пошаговые методы решения.

· Задачи стохастического программирования – задачи, в которых используются функции случайных величин.

· Векторная (многокритериальная) оптимизация изучает задачи исследования операций, в которых требуется обеспечить наибольшее (наименьшее) значение нескольким показателям эффективности в одной и той же области допустимых решений.

· Теория игр рассматривает задачи принятия решений в конфликтных ситуациях.

· Теория управления запасами изучает задачи определения объемов поставки и сроков хранения продукции.

· Сетевое планирование и управление предлагает методы планирования работ, связанных сетевыми графиками.

· Теория расписаний или теория календарного планирования рассматривает методы планирования работ во времени.

· Имитационное моделирование – моделирование систем с помощью электронной вычислительной техники.

· Моя теория – это Ваша, читатель, теория, которую Вы разработаете для решения прикладных задач, которые встанут перед Вами в ходе Вашей профессиональной деятельности. Для этого Вам потребуется использовать уже известные методы принятия решений, в первую очередь это методы решения экстремальных задач.