Деление чисел в прямых кодах
Алгоритм деления с восстановлением остатка состоит в следующем.
1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1 < 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – переполнение и переход к пункту 5.
2. Если Аi < 0, то восстанавливаем предыдущий остаток Ai=Ai+[Дт]доп.
3. Формирование очередного остатка. Ai+1=Ai∙2+[-Дт]доп если Ai+1<0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).
4. Если достигнута заданная точность частного или получен нулевой остаток Ai+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма.
5. Окончание алгоритма.
Из рассмотренного алгоритма видно следующее:
1) необходимо затрачивать время на восстановление остатка;
2) процесс деления нерегулярный, в зависимости от делимого и делителя
частное будет содержать нулей больше или меньше, и чем больше нулей, тем больше требуется времени на восстановление остатков.
Рассмотрим пример деления чисел.
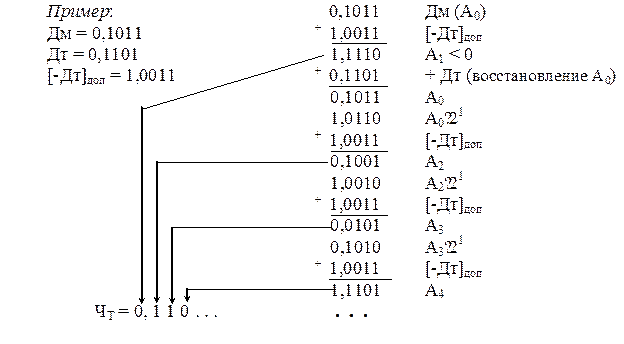
Как видно из примера, для получения остатка Аi+2 необходимо выполнить
Аi+2 = ( Ai+1 + ДT ) ∙ 21 - ДT = Ai+1 ∙ 21 + 2ДT - ДT = Ai+1 ∙ 21 + ДT
Из этого следует, что восстанавливать остаток необязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка.
Алгоритм деления без восстановления остатка.
1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1 < 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – что является признаком переполнение и ос4уществляется переход к пункту 5.
2. Формирование очередного остатка. Если Аi < 0, то Ai+1=Ai∙2+[Дт]доп, иначе Ai+1=Ai∙2+[-Дт]доп.
3. Если Аi+1 < 0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).
4. Если достигнута заданная точность частого или получен нулевой остаток Ai+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма.
5. Окончание алгоритма.
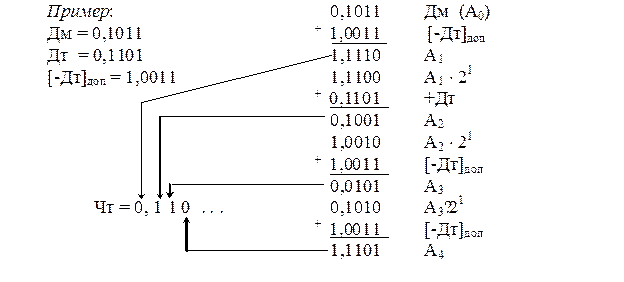
Дата добавления: 2016-01-09; просмотров: 1357;
