Умножение на два разряда множителя в дополнительных кодах
| i | i+1 | i | i+1 |
| +4Mн | -Mн | +4Mн | -2Mн |
В отличие от умножения в прямых кодах преобразованию подвергается не только пара 11, но также и пара 10. Это позволяет упростить анализ кода и формирование преобразованного множителя.
В табл. 2 приведены преобразования i и i+1 пары множителя.
Таблица 2
| i-я пара | i+1-я пара | Преобраз. пара | Алгоритм | ||||
| х | y | z | - | x¢ | y¢ | A | Г |
| - | |||||||
| - | |||||||
| - | |||||||
| - | |||||||
 1 1
| - | ||||||
 1 1
| - | ||||||
 1 1
| - | ||||||
| - |
Действия, осущестляемые при выполнении, например, алгоритмов А и Г следующие:
(1) 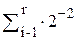 (6)
(6) 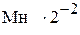
(2) 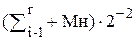 (7)
(7) 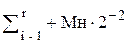
(3)  (8)
(8) 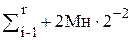
(4)  (9)
(9) 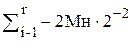
(5) 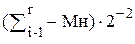 (10)
(10) 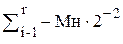
Если i+1 пара имеет старшую цифру 1, то умножение на эту пару будет соответствовать вычитанию одного или двух множителей. На рис. 9 приведена логическая схема для формирования сигнала выполняемого действия при анализе пары (xy) и старшего разряда (z) предыдущей пары при умножении чисел согласно алгоритму Г.
Как было показано выше, при умножении чисел в дополнительных кодах в общем случае необходимо вводить поправку для получения верного произведения. Однако при умножении на два разряда множителя этого выполнять не требуется. Если на умножение поступает отрицательный множитель, то при преобразовании его старшей пары происходит формирование дополнительной пары:
Мт = -10110
 [Мт]доп= 1.0 10 10
[Мт]доп= 1.0 10 10


 [Мт]допп= 01 01 01 10
[Мт]допп= 01 01 01 10
 При умножении на дополнительную пару (01) происходит вычитание одного множителя, а затем он должен быть добавлен в качестве поправки. Таким образом, тратится два такта на выполнение взаимоисключающих операций.
При умножении на дополнительную пару (01) происходит вычитание одного множителя, а затем он должен быть добавлен в качестве поправки. Таким образом, тратится два такта на выполнение взаимоисключающих операций.
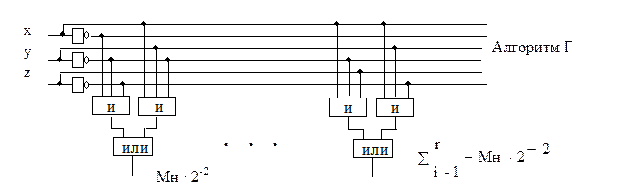
Рис. 9. Логическая схема формирования сигнала выполняемого действия
Пример:
Мн = + 0101 умножение выполним согласно
Mт = + 1100111 алгоритму Г
[Mн]доп = 0.0101
[Mт]доп = 0.1 10 01 11
Анализ пар Мт можно производить начиная от старших (при умножении по алгоритмам В и Г) и от младших разрядов (алгоритмы А и Б).

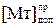
 = 10 10 10 01
= 10 10 10 01
[-2Mн]доп = 1.0110 [2Mн]доп = 0.1010
0.0000 00000000 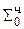
+ 0.0010 10000000 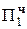 = 2MH∙2-2
= 2MH∙2-2
0.0010 10000000 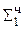
+ 1.1111 01100000 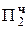 = -2MH∙2-4
= -2MH∙2-4
0.0001 11100000 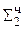
+ 0.0000 00101000 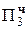 = 2MH∙2-6
= 2MH∙2-6
0.0010 00001000 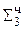
+ 1.1111 11111011 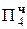 = -MH∙2-8
= -MH∙2-8
0.0010 00000011 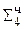 = [Mн Mт]доп
= [Mн Mт]доп
Пример:
Mн= - 0101 умножение выполним согласно
Mт = -1100111 алгоритму Б
[Mн]доп = 1.1011
[Mт]доп = 1.0 01 10 01


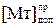 = 1.0 10 10 01
= 1.0 10 10 01
[2Mн]доп = 1.0110 [-2Mн]доп = 0.1010
0.000000 0000 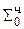
+ 1.111111 1011 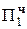 = Mн
= Mн
1.111111 1011 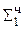
+ 0.000010 1000 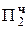 = -2Mн ∙ 22
= -2Mн ∙ 22
0.000010 0011 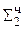
+ 1.110110 0000 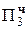 = 2Mн ∙ 24
= 2Mн ∙ 24
1.111000 0011 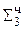
+ 0.101000 0000 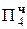 = -2Mн ∙ 26
= -2Mн ∙ 26
0.100000 0011 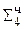 =Mн×Mт
=Mн×Mт
Дата добавления: 2016-01-09; просмотров: 845;
