Определение реакций в опорах и изгибающих моментов

В табл. 4.1 и на рис. 4.1 приведены формулы для определения реакций опор и изгибающих моментов двухопорных валов с характерными случаями нагружения [3].

Таблица 4.1

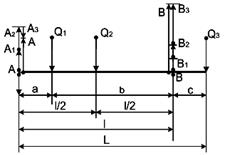1. А = А1 + А2 + А3; В = В1 + В2 + В3 (алгебраическая сумма). 2. Если приложенная сила Qn имеет направление, обратное указанному на рисунке, то реакции в опоре Аn и Bn меняют знак на обратный. 3. Qn =Аn + Bn (для проверки)
Приложенная сила	Q1	Q2	Q3
Реакция опор	+А1	+В1	+A2	+B2	–A3	+B3
Формула	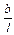Q1	Q1	A2 = B2 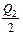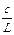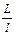=	Q3	Q3

При расчете вал принимают за балку, лежащую на шарнирных опорах. Эта расчетная схема точно соответствует действительному положению для валов на подшипниках качения. Для других опор такую расчетную схему можно применить как приближенную. При длинных несамоустанавливающихся подшипниках скольжения, расположенных по концам вала, равнодействующую реакции подшипника следует предполагать приложенной к точке, отстоящей от его кромки со стороны пролета на 1/3–1/4 длины подшипника.

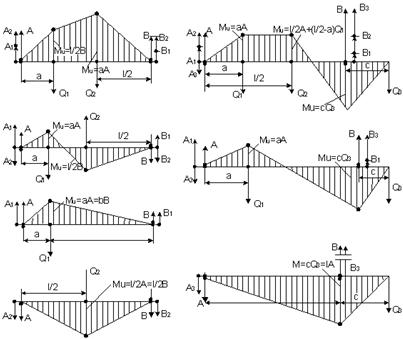
Рис. 4.1. Определение реакций опор и изгибающих моментов двухопорных валов
с приведенными случаями нагружения