ЗАКОН ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ

Изменение количества движения жидкого объёма за единицу времени равно сумме всех приложенных к нему внешних (массовых и поверхностных) сил. Количество движения и силы - величины векторные, поэтому уравнение, выражающее этот закон, является векторным. Ему соответствует система трёх уравнений, связывающих проекции векторов на оси координат.

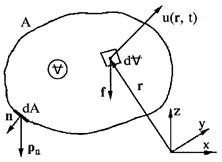
Рис.6.1. К выводу уравнения количества движения

Выделим в пространстве объём жидкости V и ограничим его контрольной поверхностью А (рис.6.1). Бесконечно малый объём dV имеет массу rdVи количество движения rudV. Количество движения всего объёма равно 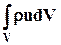. Изменение количества движения при перемещении этого объёма за единицу времени составит

(6.3.1)

Вектор внешних массовых сил, плотность распределения которых обозначим через f (х,у,z), находим аналогично: на элементарный объём dV массой rdV действует сила frdV, следовательно, внешняя массовая сила, действующая на весь объём V, равна

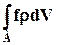(6.3.2)

Плотность распределения внешней поверхностной силы (напряжение) на контрольной поверхности А обозначим через pn, учитывая, что n - нормаль к А. Тогда на элементарную площадку dA действует сила pn dA, а на всю поверхность действует результирующая поверхностная сила

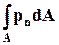. (6.3.3)

Приравняв изменение количества движения (6.3.1) сумме сил (6.3.2) и (6.3.3), получим уравнение, выражающее закон изменения количества движения:

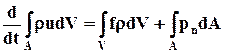. (6.3.4)

Это векторное уравнение равносильно трём скалярным уравнениям, которое можно записать, проектируя все слагаемые на координатные оси х,у,z. Например, в проекции на ось х имеем

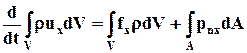. (6.3.5)

Уравнение (6.3.4) используется и в приведённом выше виде в виде гидравлического уравнения количества движения или в виде систем дифференциальных уравнений, получаемых из (6.3.4), когда контрольный объём V бесконечно мал.