СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
Упругая твёрдая среда называется линейной и изотропной в том случае, если напряжения в ней линейно связаны с деформациями, а механические свойства среды не зависят от направления. В такой среде главные оси напряжений и деформаций совпадают. Связь между напряжениями и деформациями удобно записать в системе координат, связанной с главными осями:
s1 = (l + 2G)e1 + l e2 + le3, (5.3.1)
s2 = le1+ (l + 2G ) e2 + le3, (5.3.2)
s3 = le1+ le2 + (l+2G )e3, (5.3.3)
где упругие модули l и G (модуль сдвига) называются параметрами Ламе. Свойства среды таковы, что от действия компонент деформации e возникает напряжение (l+2G)e в том же направлении и напряжения le в других взаимно перпендикулярных направлениях:
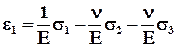 , (5.3.4)
, (5.3.4)
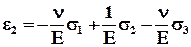 , (5.3.5)
, (5.3.5)
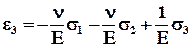 , (5.3.6)
, (5.3.6)
где Е (модуль Юнга, меняется для горных пород в пределах 10–100 ГПа) и n (коэффициент Пуассона, меняется в пределах 0.1 – 0.4) - материальные параметры среды. Главная компонента напряжения s создаёт деформацию s/E в направлении своего действия и деформации - ns/E в двух других взаимно перпендикулярных направлениях. Упругие свойства среды характеризуют, задавая l и G или E и n. Эти параметры не являются независимыми.
Одноосное напряжённое состояние. В этом случае отлично от нуля только одно главное напряжение, например, s1. s2 = s3 = 0 , тогда
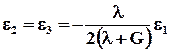 . (5.3.7)
. (5.3.7)
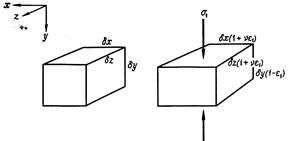 Рис. 5.6. Деформация под действием
одноосного сжатия
Рис. 5.6. Деформация под действием
одноосного сжатия
|
Отсюда видно, что напряжение s1 вызывает не только деформацию e1 в направлении своего действия, но и деформации в перпендикулярных направлениях e2 и e3. Если s1 - напряжение сжатия, то e1 - укорочение, а e2 и e3 - удлинения.
Эти деформации показаны на рис. 5.6, где элемент dxdydz стал короче в направлении оси y, но толще в направлении осей х и z. В соответствии с равенствами (5.3.4) - (5.3.6)мы можем написать
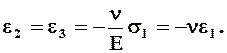 (5.3.8)
(5.3.8)
Сравнивая это равенство с (5.3.7), получаем
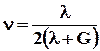 . (5.3.9)
. (5.3.9)
Из (5.3.1) и (5.3.7)находим
 , (5.3.10)
, (5.3.10)
совместно с (5.3.8) для модуля Юнга получаем
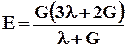 . (5.3.11)
. (5.3.11)
С помощью (5.3.9) - (5.3.11) выражаем l и G через E и n:
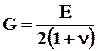 , (5.3.12)
, (5.3.12)
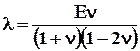 . (5.3.13)
. (5.3.13)
В случае одноосного сжатия или растяжения соотношение (5.3.8) превращается в закон Гука:
s1 = E e1. (5.3.14)
Дата добавления: 2016-01-09; просмотров: 886;
