СИЛЫ, ДЕЙСТВУЮЩИЕ НА ТЕКУЧЕЕ ТЕЛО
Движение сплошной среды вызывают силы. Они могут быть внешними и внутренними.
Внешние силы возникают в результате взаимодействия рассматриваемого тела с другими телами. Такие силы вызывают или могут вызвать изменение количества движения и кинетической энергии выделенного объёма. Типичным примером внешней силы для объектов, находящихся вблизи поверхности Земли, является сила тяжести.
Внутренние силы возникают в результате взаимодействия элементов данного тела. Они не могут изменить количество движения этого объёма, так внутри него каждая внутренняя сила уравновешивается равной ей по модулю внутренней силой, имеющей противоположное направление. Вместе с тем работа внутренних сил может изменить кинетическую и (или) потенциальную энергию рассматриваемого объёма тела. Примерами внутренних сил являются сила давления, действующая на поверхность, построенную внутри выделенного объёма жидкости; сила трения между слоями движущейся жидкости.
Внешние и внутренние силы могут быть объёмными (массовыми) и поверхностными.
Величина объёмных (массовых) сил пропорциональна объёму (массе) жидкости или газа, на который они действуют. Характеристикой объёмной (массовой) силы является плотность распределения этой силы в пространстве. Это векторная величина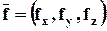 
, которая равна силе, действующей на единицу объёма (массы). Примером объёмной силы является сила тяжести. Плотность её распределения представляют в виде силы, приходящейся на единицу массы сплошной среды. Если принять оси х и у горизонтальными, а z направить вертикально вверх, то плотность распределения силы тяжести 
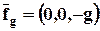, где g = 9,81 м/с2 - ускорение свободного падения. При этом вес FgобъёмаVравен
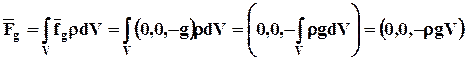. (4.1.1)
Таким образом, вес тела направлен вниз, о чём свидетельствует знак минус, и равен rgV. Величина поверхностных сил пропорциональна площади поверхности, на которую они действуют. Примером такой силы является сила взаимодействия между двумя соприкасающимися слоями жидкости, которые движутся друг относительно друга.
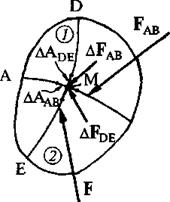Рис. 4.1. Напряжение в точке сплошной среды
|
Характеристикой поверхностной силы на заданной поверхности является плотность её распределения, которую при использовании модели сплошной среды называют напряжением. Напряжение - величина векторная.
Напряжение в данной точке фиксированной поверхности обычно проектируют на нормаль к ней и на касательную плоскость, при этом различают нормальные и касательные напряжения.
Физически поверхностные силы обусловлены силами ближнего взаимодействия молекул, расположенных по разные стороны от рассматриваемой поверхности, и переносом молекул сквозь эту поверхность в процессе их теплового движения.
4.2. НАПРЯЖЁННОЕ СОСТОЯНИЕ В ТОЧКЕ СПЛОШНОЙ СРЕДЫ. ТЕНЗОР НАПРЯЖЕНИЙ
Разделим произвольную часть сплошной среды поверхностью АВ на две части (Рис.4.1), при этом часть 1 будет действовать на часть 2 с силой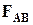 
. Обозначив площадь поверхности АВ через ААВ , среднее напряжение на АВ выразим вектором, имеющим то же направление, что и :
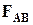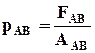. (4.2.1)
Обозначим произвольную малую часть поверхности АВ, содержащую точку М, через DААВ; на неё будет действовать сила D 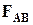. Стягивая D ААВ в точку М, получаем вектор напряжения в этой точке:
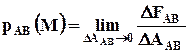. (4.2.2)
Проведя через точку М другую поверхность, например, ДЕ,можно с помощью таких же рассуждений получить другой вектор напряжения рДЕ (М).
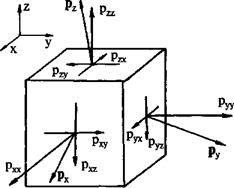Рис. 4.2. Обозначения напряжений в сплошной среде и их проекций на оси координат
|
Таким образом, вектор напряжения (плотности распределения поверхностной силы) на поверхности, проходящей через данную точку, зависит от ориентации этой поверхности.
Выделим в пространстве элементарный куб, грани которого параллельны координатным плоскостям (рис.4.2), и обозначим векторы напряжений на этих гранях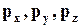 
, где индекс соответствует координатной оси, к которой грань куба перпендикулярна.
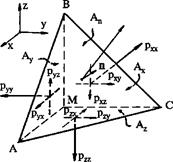Рис. 4.3. Определение напряжения на произвольно-ориентированной площадке
|
Для обозначения проекции вектора напряжений на какую-либо координатную ось введём второй подстрочный индекс, соответствующий этой оси. Например, рух - это проекция вектора напряжения ру на ось х. Как видно из рисунка, рхх, руу, рzz - нормальные напряжения; рху, рхz, рух, рzх, рzу - касательные.
Выделим в сплошной среде элементарную (с точки зрения напряжений) пирамиду с вершиной в точке М (рис.4.3.), три грани которой перпендикулярны осям координат х, у, z, а ориентация четвёртой грани АВС определяется единичным вектором нормали n,имеющим проекции на координатные оси :
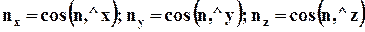(4.2.3)
Обозначим площади граней пирамиды, ортогональных осям х,у, z, соответственно Ах, Ау, Аz , площадь грани АВС обозначим Аn , а напряжение на ней - pn. Отметим, что проекции pn на координатные оси рnх, рnу, рnz не являются ни нормальными, ни касательными напряжениями. Исходя из геометрических соотношений, получим
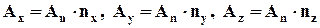. (4.2.4)
Считаем линейные размеры пирамиды бесконечно малыми; при этом объёмные силы, действующие на пирамиду, это бесконечно малые величины третьего порядка, и ими можно пренебречь, по сравнению с поверхностными силами, которые являются бесконечно малыми второго порядка. Имея это в виду, приравняем нулю сумму проекций на ось х всех поверхностных сил, действующих на пирамиду АВСМ:
. (4.2.5)
Подставляя (4.2.4) в (4.2.5) и сокращая на Аn, получаем проекцию вектора pn на ось х
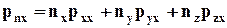. (4.2.6)
Исходя из равенства нулю сумм проекций сил на координатные оси у и z, найдём две другие проекции pn:
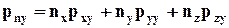; (4.2.7)
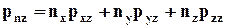. (4.2.8)
Тем самым определим вектор напряжений на грани АВС:
.
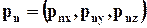Таким образом, зная три вектора напряжений на взаимно ортогональных площадках и используя уравнения статистики, можно найти напряжение на произвольно ориентированной площадке. Следовательно, три вектора напряжений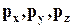 
полностью характеризуют напряжённое состояние в данной точке пространства.
Представленную в виде квадратной матрицы совокупность девяти проекций на координатные оси трёх векторов, определяющих напряжения в точке сплошной среды, обозначим буквой П:
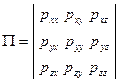. (4.2.9)
Используя матричную форму записи, можно представить равенства (4.2.3), (4.2.4), (4.2.5) в виде
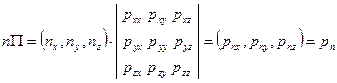. (4.2.10)
Если задать другую систему координатных осей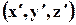 
, то соответствующие этим осям три вектора напряжений также характеризовали бы напряжённое состояние в этой же точке М. Матрицы, которые определяют какую-либо физическую величину, т.е. величину, не зависящую от выбора системы координат, называют тензорами. Эти матрицы при введении новой системы координат преобразуются определённым образом.
1.Составляющие матрицы, образующие строки, считаются компонентами векторов, относящихся к площадкам, перпендикулярным соответствующим координатным осям (например, в нашем случае строки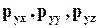 
являются компонентами вектора напряжения ру, действующего на площадке, перпендикулярной оси у).
2.Проекции на координатные оси х, у, z векторов, действующих на площадке, перпендикулярные новым координатным осям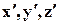 
, находим, считая, что векторы представляют собой плотности распределения поверхностных сил (напряжений) и что выполняется условие статики, т.е. по уравнениям (4.2.6)-(4.2.8). В общем случае матрица необязательно характеризует напряжённое состояние, поэтому векторы, составляющие строки матрицы, могут быть и несиловыми характеристиками.
3.Определив проекции векторов 
на старые координатные оси х, у, z, исходя из геометрических соотношений, находим их проекции на новые координатные оси и из этих проекций образуем матрицу тензора в новой системе координат.
В тензорных обозначениях равенство (4.2.9) можно представить в виде
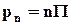(4.2.11)
Как доказывается в тензорном исчислении, сумма диагональных элементов матрицы не зависит от системы координат, в которой она записана. Эта величина называется линейным инвариантом тензора. Для тензора напряжений П имеем
.
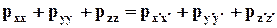Сумма нормальных напряжений по трём взаимно ортогональным площадкам не зависит от ориентации их в пространстве. Благодаря этому важную роль в механике вязкой жидкости играет гидродинамическое давление р, которое определяется равенством
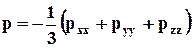(4.2.12)
и может рассматриваться как скалярная величина.
Рассматривая равновесие элементарного (в отношении напряжений) кубика, представленного на рис. 4.2, из равенства нулю суммы моментов поверхностных сил относительно трёх его взаимно ортогональных рёбер (пренебрегая при этом моментом от массовых сил как величиной более высокого порядка малости) получим
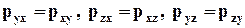. (4.2.13)
Это свойство равенства касательных напряжений свидетельствует о симметричности матрицы тензора напряжений.
В соответствии с определением (4.2.2) единицей напряжения является
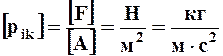ºПа.
На практике часто пользуются производными от паскаля единицами: гектопаскаль (гПа = 100 Па), килопаскалями (кПа = 100 Па) и мегапаскалями (МПа = 1000 000 Па). В этих же единицах измеряется и гидродинамическое давление р.
Дата добавления: 2016-01-09; просмотров: 998;