ЦИРКУЛЯЦИЯ СКОРОСТИ. ВИХРЬ ВЕКТОРА СКОРОСТИ
Если в поле 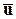 мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S,то линейный интеграл
мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S,то линейный интеграл
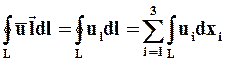
называется циркуляцией скорости,а вектор, определяемый в виде
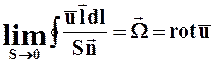 ,
,
называется вихрем или ротором скорости.
В данном случае 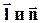 - единичные векторы, направленные соответственно по касательной к Lи по нормали к поверхности S.
- единичные векторы, направленные соответственно по касательной к Lи по нормали к поверхности S.
В декартовой системе координат вихрь скорости вычисляется по формуле
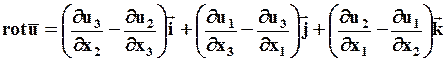 .
.
На основании теоремы Стокса имеет место равенство
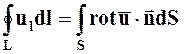 .
.
Проводя аналогию с механикой твердого недеформируемого можно отметить, что при движении элементарного объема жидкости можно выделить два вида движения, которые уже изучались в курсе теоретической механики - поступательное движение твердого тела со скоростью полюса и вращение его вокруг полюса. Для жидкости дополнительным видом движения является деформационное. Поэтому иногда подразделяют движение элементарного объема жидкости на квазитвёрдое(поступательное и вращательное) и деформационное.
Из шести составляющих тензора, описывающего вращение жидкого объема вокруг полюса, только три отличаются друг от друга абсолютной величиной. Каждая из них определяет значение мгновенной угловой скорости вращения вокруг оси, параллельной одной из координатных осей. Эти угловые скорости wx,wy,wz можно рассматривать как проекции на соответствующие координатные оси вектора w, определяющего угловую скорость вращения элементарного объема жидкости при его перемещении в трехмерном пространстве. Например, как было показано выше,
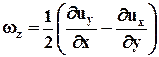 .
.
Обратим внимание на то, что буква z не входит в качестве индекса или координаты в правую часть равенства, определяющего wz. Аналогично записываются выражения для wz и wу. Вектор w в матричной форме имеет вид
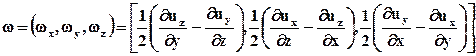 . (3.5.1)
. (3.5.1)
В векторном анализе вместо w рассматривают вектор 2w, который обозначают rot u и называют вихрем вектора u (или вихрем скорости):
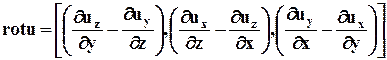 . (3.5.2)
. (3.5.2)
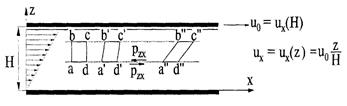 Рис. 3.10. Сдвиговое продольно-однородное течение (течение Куэтта)
Рис. 3.10. Сдвиговое продольно-однородное течение (течение Куэтта)
|
Следует обратить внимание, что ранее рассматривалось лишь перемещение объема за бесконечно малые интервалы времени Dt. Если рассматривать конечные интервалы времени, то, например, после поворота с угловой скоростью w за время Dt элементарный объем жидкости займет другие точки в поле скорости, и за следующий отрезок времени его угловая скорость может измениться. В результате даже при наличии во всех точках скорости 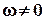 и rot u ¹ 0 (такие поля называются вихревыми) может оказаться, что при перемещении на конечные расстояния элементарного объема жидкости поворот его вокруг полюса не будет восприниматься как вращение в обычном смысле. Например, при сдвиговом продольно-однородном течении (течении Куэтта), представленном на рис. 3.10 с полем скорости
и rot u ¹ 0 (такие поля называются вихревыми) может оказаться, что при перемещении на конечные расстояния элементарного объема жидкости поворот его вокруг полюса не будет восприниматься как вращение в обычном смысле. Например, при сдвиговом продольно-однородном течении (течении Куэтта), представленном на рис. 3.10 с полем скорости 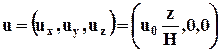 , имеем, что только
, имеем, что только 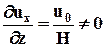 , а все остальные составляющие тензора grad u равны нулю.
, а все остальные составляющие тензора grad u равны нулю.
Отметим, что, хотя мгновенная угловая скорость этого объема отлична от нуля,
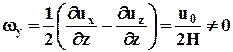 ,
,
при перемещении объема abсd на большое расстояние его поворот вокруг точки а не воспринимается как вращение.
В том случае, когда все проекции скорости 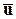 могут быть определены одной функцией j (х1, х2, х3, t) в виде
могут быть определены одной функцией j (х1, х2, х3, t) в виде 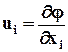 , то есть
, то есть 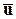 = grad j , то говорят, что поле скоростей потенциальное, а функция j - потенциал скорости.
= grad j , то говорят, что поле скоростей потенциальное, а функция j - потенциал скорости.
Проекция скорости vl на любое направление l определяется производной dj/dl .
Необходимым и достаточным условием существования потенциальных течений являются равенства ( 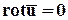 ):
):
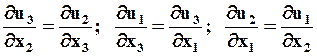 .
.
Следовательно,безвихревое течение жидкости потенциально.
Дата добавления: 2016-01-09; просмотров: 1930;
