ПОЛЯ В ГИДРОДИНАМИКЕ
При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики.
В общем случае поле является пространственным (трёхмерным), иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат.
Если физические величины не зависят от времени, то поле называют стационарным, в противном случае - нестационарным.
При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов.
Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду.
Скалярным называют поле, которое в каждой точке пространства характеризуют одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры).
Основное свойство скалярной функцииа(х1 ,х2 ,х3)состоит в том, что её численное значение не меняется при преобразовании координат.
Если перейти от старой х1 ,х2 ,х3 к новой х¢1 ,х¢2 ,х¢3 системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются:
а (х¢1 ,х¢2 ,х¢3) = а (х1 ,х2 ,х3).
Векторным называют поле, которое в каждой точке пространства характеризуется величиной и направлением.
Например, поле скоростей жидкости. Вектор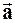 в пространстве трёх измерений может быть задан тремя компонентами:
в пространстве трёх измерений может быть задан тремя компонентами:
а1(х1 ,х2 ,х3), а2(х1 ,х2 ,х3), а3(х1 ,х2 ,х3),
то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:
а ÜÞ 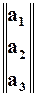
Введём новую декартову систему координат с тем же началом, но с другим направлением осей.
Пусть lij - направляющий косинус оси x¢j относительно оси xi (i = 1,2,3; j = 1,2,3).Вычислим проекции того же вектора на новые оси координат:
a¢1 = l11 a1 + l21 a2 + l31 a3;
a¢2 = l21 a1 + l22 a2 + l23 a3;
a¢3 = l31 a1 + l32 a2 + l33 a3.
Следовательно, вектор подчиняется определённому закону преобразования его компоненти отличается от скалярной величины, численное значение которой не меняется при преобразовании координат.
То есть,сам вектор не меняется в новых координатах, а меняются его компоненты.
Это выражение можно представить в индексной форме записи как сумму:
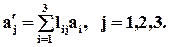
Или ещё более короткой 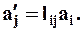
При такой записи пользуются двумя правилами:
1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.
2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3.
Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений.
Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля.
Многие задачи физики и механики сплошной среды приводят к понятию тензора. Тензор, хотя и является обобщением понятия вектора, имеет гораздо более сложный характер. Разница заключается в том, что вектор просто интерпретируется геометрически, у тензора такого наглядного представления не существует.
Описание происходит в прямолинейных (декартовых) системах координат. Координаты обозначаем х1, х2, х3, единичные векторы по осям - i1,i2, i3.
Предположим, что в результате вращения осей координат как единого целого вокруг начала координат, мы перешли к новой системе координат Ox1´x2´x3´. Обозначим косинус угла между осями xi и x´k старой и новой системы aik = cos (x´i^xk). Для удобства пользования дальнейшими формулами приводим таблицу.
Таблица 3.1
| х1 | х2 | х3 | |
| х´1 | a11 | a12 | a13 |
| х´2 | a21 | a22 | a23 |
| х´3 | a31 | a32 | a33 |
Теперь перейдём к определению тензора. Пусть каждому направлению 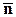 соответствует вектор
соответствует вектор 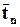 (не обязательно коллинеарный n).
(не обязательно коллинеарный n).
Направлениям осей соответствуют векторы 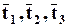 , разложение которых опишем подробно:
, разложение которых опишем подробно:
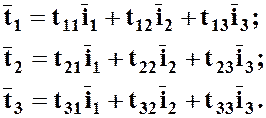 (3.6.1)
(3.6.1)
Если векторы 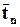 для любого направления
для любого направления 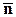 выражаются лишь через 3 вектора
выражаются лишь через 3 вектора 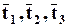 согласно формуле
согласно формуле
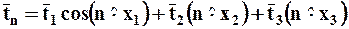 , (3.6.2)
, (3.6.2)
то множество векторов 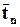 образует тензор Т.
образует тензор Т.
Обозначим векторы, определяемые тензором для направлений новых осей 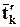 . Подставляя в предыдущее выражение (2.6.2) вместо
. Подставляя в предыдущее выражение (2.6.2) вместо 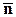 направления новых осей (по очереди), получим:
направления новых осей (по очереди), получим:
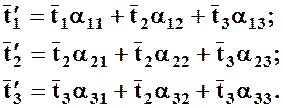 (3.6.3)
(3.6.3)
Эти условия равносильны (2.6.2) и их можно взять за новое определение тензора, если для каждой системы координат имеется тройка векторов 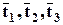 , преобразующаяся по формулам (2.6.3) в тройку
, преобразующаяся по формулам (2.6.3) в тройку 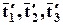 , отвечающую другой системе координат, то этим определяется тензор.
, отвечающую другой системе координат, то этим определяется тензор.
Аналогичное определение можно дать и для вектора, если в уравнении (2.6.3) заменить векторы на проекции вектора. Поэтому тензор является обобщением вектора. Формулы (2.6.3) можно записать в сокращённом виде
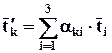 .
.
Тензор определяется векторами 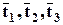 , которые в свою очередь определяются своими компонентами (3.6.1). Поэтому тензор вполне задаётся 9 числами, которые называются компонентами тензора, и обычно записываются в виде
, которые в свою очередь определяются своими компонентами (3.6.1). Поэтому тензор вполне задаётся 9 числами, которые называются компонентами тензора, и обычно записываются в виде
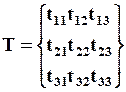 .
.
Из (2.6.1) и (2.6.3) можно получить формулы преобразования компонент тензора при переходе к новой системе координат:
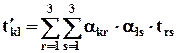 , (3.6.4)
, (3.6.4)
где t´kl – компоненты в новой системе.
Эти формулы можно также взять за определение тензора.
Простейшими примерами являются нулевой и единичный тензоры.
Согласно (2.6.4) у нулевого тензора в любой системе координат компоненты равны 0.
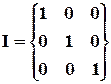 .
.
Для того, чтобы в дальнейшем не испытывать трудностей при использовании тензоров, запишем некоторые математические правила.
Дата добавления: 2016-01-09; просмотров: 951;
