Линейно-упругое тело называется иначе Гуковским телом.
Относительное изменение объёма (дилатация D) определяется в этом случае выражением
D = e + e2 + e3 = e1(1 - 2n). (5.3.15)
Из формулы видно, что уменьшение объёма, происходящее за счёт сокращения размера в направлении действия напряжения, компенсируется увеличением объёма за счёт расширения в перпендикулярных направлениях. Из выражения (5.3.15) можно определить коэффициент Пуассона для несжимаемой среды, объём которой не меняется под действием приложенного напряжения. Чтобы это реализовать, при одноосном сжатии n должно быть равно ½. Под действием одноосного сжатия несжимаемая среда сокращается в направлении приложенного напряжения и расширяется на величину, вдвое меньшую в каждом из перпендикулярных направлений.
Одноосная деформация. Состояние одноосной деформации характеризуется тем, что отличной от 0 является только одна главная компонента деформации, например, e1.Тогда (5.3.1) - (5.3.3) дают
s1= (l + 2G)e1, (5.3.16)
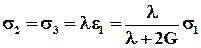 , (5.3.17)
, (5.3.17)
а (5.3.4) - (5.3.6) упрощаются следующим образом:
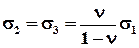 , (5.3.18)
, (5.3.18)
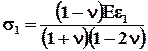 . (5.3.19)
. (5.3.19)
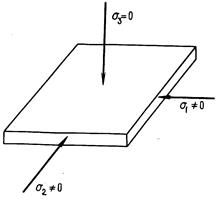 Рис. 5.7. Плоское напряжённое состояние
Рис. 5.7. Плоское напряжённое состояние
|
Плоское напряжённое состояние. Возникает тогда, когда имеется только одно нулевое главное напряжение, например, s3 = 0,s2 ¹ 0,s 1¹ 0. Тонкая пластина нагружена с боков. Определим компоненты деформации (5.3.4) - (5.3.6)
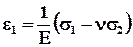 , (5.3.20)
, (5.3.20)
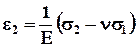 , (5.3.21)
, (5.3.21)
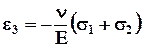 . (5.3.22)
. (5.3.22)
Плоская деформация. В этом случае равна нулю только одна главная деформация, например, e3 = 0.
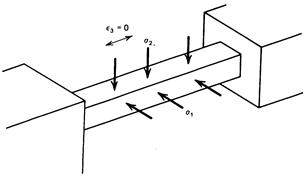 Рис. 10. Пример плоской деформации
Рис. 10. Пример плоской деформации
|
На (рис.5.7) длинная балка жёстко зажата между двумя стенками, которые не позволяют ей расширяться или сжиматься в продольном направлении. Кроме того, вдоль всей длины на балку действуют равномерно распределённые напряжения s1и s2. (5.3.1)-(5.3.3) в этом случае становятся:
s1 = (l + 2G)e1 + le2; s2 = le1 + (l + 2G)e2; s3 = l(e1 + e2).
Из равенства (5.3.6) следует s3 = n(s1 + s2 ),что совместно с (5.3.7) и (5.3.9) даёт
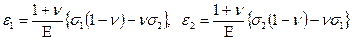 .
.
Дата добавления: 2016-01-09; просмотров: 1004;
