ОСНОВЫ ГИДРОДИНАМИКИ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Задачи гидродинамики делятся на два основных класса: внутренние и внешние. К внешним задачам относятся задачи обтекания тела потоками жидкости или газа, или о движении тела в жидкой или газообразной среде. Внешними задачами являются задачи, связанные с полётами самолётов, снарядов и других тел, движущихся в атмосфере. Внутренние задачи занимаются движением жидкости в каналах. В этот класс задач входят такие, как:

1. течение жидкостей в трубопроводах (водопровод, газо-и нефтепроводы, кровеносная система, тепло и газоснабжение);

2. течение воды в открытых каналах и реках (ирригационные и осушительные системы, расчёт паводков, судопропускные сооружения и т.д.).

При решении внешней задачи основной акцент делается на определение силового взаимодействия потока и тела. Определение силы, действующей со стороны набегающего потока, или силы сопротивления движению тела в жидкости - цель таких задач. Поэтому при анализе и решении внешних задач, как правило, используются уравнения, выражающие закон изменения количества движения: дифференциальные уравнения Навье - Стокса или Рейнольдса, а также интегральные формы этого закона.

При решении внутренней задачи чаще всего стараются определить потери энергии в потоке жидкости. Здесь используются уравнения, выражающие закон изменения кинетической энергии, чаще всего в виде различных форм уравнения Бернулли.

В основе гидродинамики, как части гидромеханики, положены четыре основных закона механики:

закон сохранения массы;

закон изменения количества движения (импульса);

закон изменения момента количества движения;

закон изменения кинетической энергии.

Эти законы формулируются для конечных объёмов ( размеры ограничены и оговорены). Законы гидродинамики для конечных объёмов часто упрощаются с учётом конкретных условий на поверхностях, ограничивающих данный объём. Такие упрощенные уравнения используются в разделе, называемом гидравликой. По сути это теоретические основы технической механики жидкости. Они особенно эффективны, когда исследуются интегральные (осреднённые по времени и пространству) гидромеханические характеристики потоков.

В том случае, когда есть необходимость определять гидромеханические характеристики и величины в каждой точке объёма жидкости, используют дифференциальные уравнения. Они тоже являются фундаментальными законами механики, но относятся к точке сплошной среды. Если эти уравнения дополнить каким-либо реологическим законом, то можно определить структуру поля скорости и напряжённое состояние в любой точке потока жидкости.

Практическое использование этих уравнений, в зависимости от изложенных здесь подходов, преобразуется из одного вида в другой с помощью теоремы Остроградского - Гаусса. Так при выводе гидравлических уравнений объёмные интегралы заменяются на поверхностные с тем, чтобы использовать особенности условий на поверхностях, ограничивающих поток, для упрощения уравнений. При выводе дифференциальных уравнений, наоборот, поверхностные интегралы заменяются на объёмные, чтобы можно было исследовать гидромеханические величины в точках внутри потока. При этом условия на границах потока вводятся как граничные или краевые условия для дифференциальных уравнений.

6.2.ЗАКОН СОХРАНЕНИЯ МАССЫ

Выделим в пространстве контрольный объём V, ограниченный произвольной контрольной поверхностью А. Пусть плотность жидкости r зависит и от времени, и от координат, т.е. .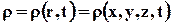

Масса бесконечно малого объёма dV, расположенного в точке с координатами 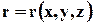, в момент времени t равна 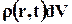. Масса объёма V жидкости, находящейся внутри замкнутой поверхности А, равна

. (6.2.1)

Согласно закону сохранения массы, при движении жидкого объёма его масса остаётся неизменной. Изменение во времени гидромеханической характеристики, относящейся к движущемуся жидкому объёму, который содержится в начальный момент внутри контрольной поверхности А, выражается в виде субстанциональной производной от этой характеристики. Представим закон сохранения массы, используя эту производную

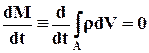. (6.2.2)

Уравнение (6.2.2) используют в качестве уравнения неразрывности при решении одномерных задач, а также в виде дифференциальных уравнений, когда контрольный объём бесконечно мал.