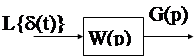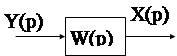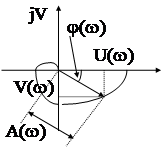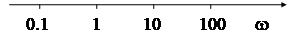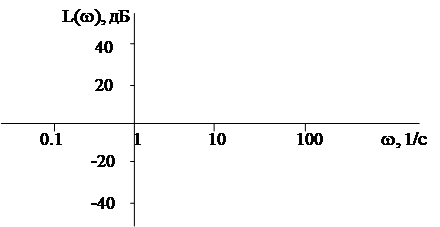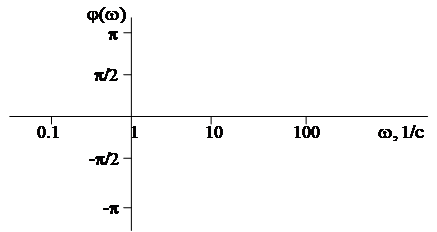Весовой или импульсной переходной функцией АС называется ее реакция на единичный импульс при нулевых начальных условиях.

Обозначается - g(t) и характеризует способность системы к возврату в исходное невозмущённое состояние.

Изображение по Лапласу G(p)= W(p)L{d(t)}=W(p) совпадает с передаточной функцией. Вторая теорема Хэвисайда для нахождения g(t) по изображению G(p) имеет вид:

,

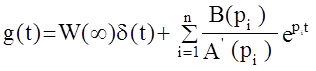опять здесь р_i - простые (не кратные) корни А(р).

Пример: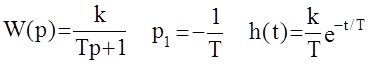

Свойства весовой функции:

1) Реакция системы на произвольный входной сигнал y(t):

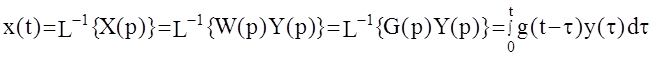
Данный интеграл называется интегралом Дюамеля, он позволяет получить выходной сигнал по известным весовой функции и входному сигналу.

Пример: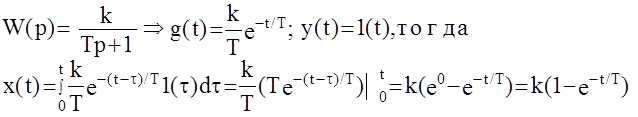

Получили переходную функцию апериодического звена.

2) Предельные значения весовой функции:

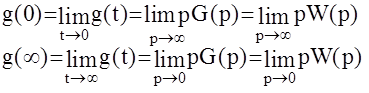
3) Связь с переходной функцией:

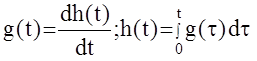
2.4Частотные характеристики линейных стационарных АС

Пусть на вход линейной стационарной АС с одним входом и одним выходом

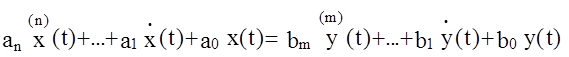
действует гармонический входной сигнал частоты w. В общем виде этот сигнал может быть представлен в комплексной показательной форме:

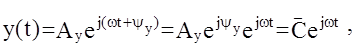
здесь А_у, w, y_у - амплитуда, частота и начальная фаза входного сигнала; 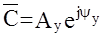- комплексная амплитуда входного сигнала.

Для линейных стационарных АС выходной установившийся сигнал будет также гармоническим частоты w, но другой амплитуды и фазы:

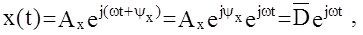
где 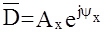- комплексная амплитуда выходного сигнала. Подставим выражения y(t) и x(t) в исходный оператор системы:

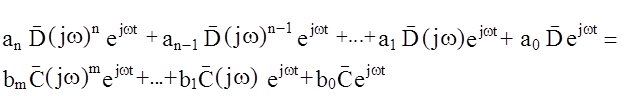
или:

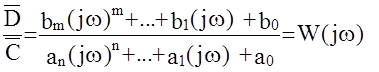
Отношение вынужденной составляющей выходного сигнала к гармоническому входному сигналу, представленным в комплексной показательной форме, называется амплитудно-фазовой частотной характеристикой (АФЧХ) системы или комплексным коэффициентом усиления.

АФЧХ определяет зависимость амплитуды и фазы выходного сигнала АС в зависимости от амплитуды, фазы и частоты входного сигнала. Для определения АФЧХ необходимо в выражении для передаточной функции заменить переменную р на мнимую переменную jw. АФЧХ - это комплексное число, на комплексной плоскости изображается вектором. При изменении частоты от 0 до ¥ конец этого вектора описывает некоторую кривую, называемую годографом АФЧХ или просто АФЧХ системы.

2.5Типы частотных характеристик.

Как любое комплексное число АФЧХ может быть записана в показательной или алгебраической формах:

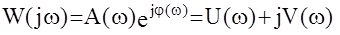
Функции А(w), j(w), U(w), V(w) представляют собой различные типы частотных характеристик.

А(w)-амплитудно-частотная характеристика - АЧХ;

j(w)-фазо-частотная характеристика - ФЧХ;

U(w)-вещественная частотная характеристика-ВЧХ;

V(w)-мнимая частотная характеристика - МЧХ.

Связь между этими характеристиками устанавливается так:

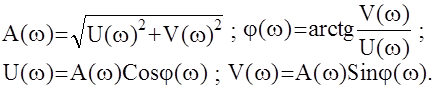
Определим физический смысл этих характеристик.

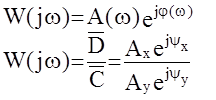Þ

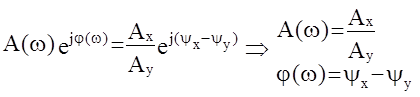
Очевидно, если амплитуда А_у и фаза Y_у входного сигнала остаются неизменными, то АЧХ и ФЧХ системы представляют собой зависимости амплитуды А_х и фазы Y_х выходного сигнала в зависимости от частоты входного сигнала. Эти характеристики обычно и используются на практике. Таким образом, АЧХ системы- это отношение амплитуды выходного гармонического сигнала к амплитуде входного гармонического сигнала, вычисленное для различных частот w входного сигнала.

ФЧХ системы - это разность фаз выходного и входного сигналов для различных частот.

Эти свойства используются при нахождении частотных характеристик линейных АС, когда известны их передаточные функции. С другой стороны, если на вход системы с известными частотными характеристиками А(w) и j(w) подать гармонический входной сигнал

А_у Sin(wt+Y_у), то установившийся входной сигнал будет также гармоническим А _хSin(wt+Y_х), а его параметры определяютс так:

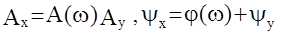
На практике частотные характеристики чаще всего представляются не аналитическими выражениями, а графиками. Причем используются не просто частотные характеристики, а логарифмические ЧХ, построенные в логарифмическом масштабе частот.Использование такого масштаба позволяет на одном графике показать изменение характеристик системы в очень большом диапазоне частот. Обычно применяются логарифмическая амплитудная частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ).

ЛАЧХ - это характеристика, вычисленная по формуле:

L(w) = 20lgA(w)

и построенная в логарифмическом масштабе частот.

За единицу логарифмического масштаба частот принята декада. Декада - это отрезок оси частот, на котором она изменяется в 10 раз. Очевидно, что «0» на оси частот располагается слева в «-¥» .

За единицу масштаба по оси ординат принят 1 децибел (дБ). 1дБ соответствует коэффициенту усиления k₀ такому, что 20lgk₀ = 1(отсюда k₀=10^0.05). Поэтому ЛАЧХ, вычисленная по формуле 20lgA(w), будет выражаться в дБ (в ТАУ эти децибелы никакого отношения к акустике не имеют).

Логарифмическая фазовая частотная характеристика (ЛФЧХ) - это фазочастотная характеристика j(w) системы, построенная в логарифмическом масштабе частот.

Оси координат, при построении логарифмических частотных характеристик (ЛЧХ) обычно принято располагать так (ось ординат всегда проходит через точку w=1 и графики располагают точно друг под другом).

2.6.Частотные характеристики соединений звеньев

Как уже было отмечено ранее, любая сколь угодно сложная АС может быть представлена в виде последовательного соединения элементарных звеньев, динамические характеристики которых определяются достаточно просто. Возникает вопрос о том, как, зная характеристики отдельных звеньев, входящих в систему, определить динамические характеристики всей системы в целом? Временные характеристики определяются по известной теореме Хэвисайда, а частотные могут быть определены с использованием свойств ЛЧХ.

Как известно, передаточная функция последовательного соединения звеньев равна 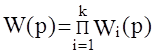, а соответствующая АФЧХ:

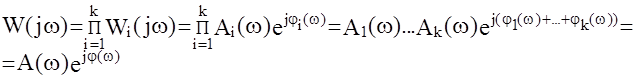
Здесь А(w)=А₁(w)А₂(w)...А_k(w) - АЧХ последовательного соединения k звеньев; j(w)=j₁(w)+....+j_k(w) - ФЧХ последовательного соединения. Так как частотные характеристики обычно задаются графически, то нахождение АЧХ системы в виде графического произведения достаточно неудобно, поэтому рассмотрим как в этом случае определяется ЛАЧХ системы:

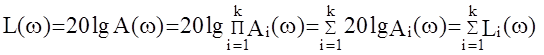
Таким образом, ЛАЧХ (также и ЛФЧХ) последовательного соединения звеньев равна сумме соответствующих характеристик этих звеньев, что позволяет широко применять графические способы определения частотных характеристик сложных систем.