Электропроводность металлов
Дрейф электронов определяет величину плотности электрического тока в кристалле. Построим мысленно в объеме проводника цилиндр с основанием, равным единице площади, и образующей, равной скорости дрейфа vдр и направленной вдоль дрейфа (рис. 4.2). Все электроны, заключенные в этом цилиндре, в течение 1 с пройдут через его основание и образуют ток с плотностью
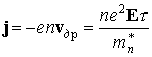 , (4.8)
, (4.8)
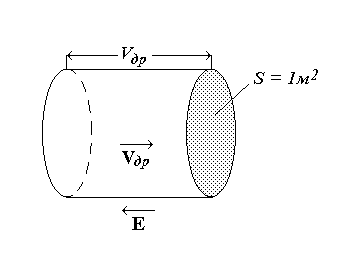 Рис. 4.2. К расчету удельной электропроводности металла
Рис. 4.2. К расчету удельной электропроводности металла
|
здесь n - концентрация электронов проводимости.
Выражение (4.8) имеет форму закона Ома. Электропроводность n металлов (электронная электропроводность) есть по определению коэффициент пропорциональности между плотностью тока j и напряженность электрического поля Е, т.е. j=nЕ. Следовательно, из (4.6) и (4.8) имеем
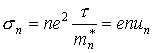 . (4.9)
. (4.9)
Величина n, обратная удельной электропроводности, называется удельным электросопротивлением:
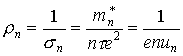 . (4.10)
. (4.10)
Таким образом, электропроводность (электросопротивление) металлов обусловлена концентрацией электронов проводимости и их подвижностью. Концентрация электронов проводимости металлов от температуры практически не зависит. Подвижность электронов в кристалле определяется механизмами рассеяния электронов проводимости и существенно зависит от температуры. Как указывалось выше, электросопротивление большинства металлов обусловлено рассеянием электронов на различных видах нарушений регулярной кристаллической структуры решетки. Эти нарушения можно разделить на две группы: 1) тепловые колебания ионов кристаллической решетки (фононы); 2) статические дефекты кристаллической решетки (точечные дефекты, дислокации, статические геометрические искажения и др.).
В соответствии с этим и электросопротивление реального металла, в котором в той или иной степени присутствуют все виды рассеяния электронов проводимости, приближенно представляют в виде двух слагаемых
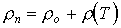 , (4.11)
, (4.11)
здесь о - часть удельного электросопротивления, обусловленная рассеянием электронов на статических дефектах, (T) - часть удельного электросопротивления, обусловленная рассеянием на фононах.
При комнатной температуре и выше основное значение имеет взаимодействие электронов с решеточными фононами (электрон-фононное рассеяние). Этим механизмом рассеяния обусловлена хорошо известная линейная зависимость удельного электросопротивления металлов от температуры:
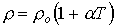 .
.
Постоянная называется температурным коэффициентом сопротивления.
 Рис. 4.3. Зависимость удельного электро-сопротивления металла от температуры
Рис. 4.3. Зависимость удельного электро-сопротивления металла от температуры
|
При очень низких температурах, когда влиянием тепловых колебаний на рассеяние электронов можно пренебречь, сопротивление металлов практически перестает зависеть от температуры (рис. 4.3). Предельное значение о, к которому стремится сопротивление металловпо мере понижения температуры к абсолютному нулю, называется остаточным сопротивлением. Остаточное сопротивление металлов является очень важной характеристикой, чувствительной к концентрации дефектов в решетке. Например, для кристалла меди чистоты 99,999% остаточное сопротивление приблизительно в 1000 раз меньше удельного электросопротивления при комнатной температуре. Для цинка чистоты 99,99999% (один из наиболее чистых полученных в настоящее время металлов) это отношение составляет 105.
В промежуточной области температур электросопротивление металлов определяется приближенной формулой:
 , (4.12)
, (4.12)
здесь A и B - величины, не зависящие от температуры.
Дата добавления: 2016-01-09; просмотров: 1556;
