Уровень Ферми в полупроводниках

Понятия энергии Ферми и уровня Ферми были введены ранее для металлов. Поскольку в полупроводниках функция распределения электронов по состояниям имеет тот же вид, что и в металлах, то энергия Ферми в полупроводниках имеет тот же физический смысл: энергия Ферми - это максимально допустимая энергия, ниже которой при нулевой абсолютной температуре все энергетические уровни заняты [f(E) = 1], а выше которой все уровни пусты [f(E) = 0]. Для полупроводников, у которых при абсолютном нуле валентная зона полностью заполнена, а зона проводимости совершенно свободна, функция распределения имеет разрыв. Следовательно, уровень Ферми в полупроводнике должен лежать при абсолютном нуле в запрещенной зоне.

Для собственного полупроводника концентрации электронов и дырок равны (n = p), т.к. каждый электрон, покинувший валентную зону, создает одну дырку. Приравнивая равенства (3.17) и (3.19), получим

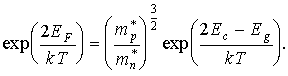
Разрешая последнее равенство относительно Е_F, получим

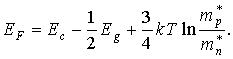(3.23)

Если эффективные массы электронов и дырок равны [ 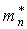= 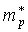, 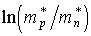= 0] уровень Ферми собственного полупроводника при любой температуре располагается посередине запрещенной зоны.

Температурная зависимость положения уровня Ферми в собственном полупроводнике определяется третьим слагаемым в уравнении (3.23). Если эффективная масса дырки в валентной зоне больше эффективной массы электрона в зоне проводимости, то уровень Ферми смещается с повышением температуры ближе к дну зоны проводимости. В противоположном случае уровень Ферми смещается к потолку валентной зоны. Положение уровня Ферми в собственном полупроводнике с изменением температуры схематически показано на рис. 3.5.

Для большинства полупроводников эффективная масса дырки не намного превышает эффективную массу электрона и смещение уровня Ферми с изменением температуры незначительно. Однако у антимонида индия (InSb) 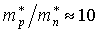, а ширина запрещенной зоны невелика (E_g = 0,17 эВ), так что при Т > 450 K уровень Ферми входит в зону проводимости. При этой температуре полупроводник переходит в вырожденное состояние.

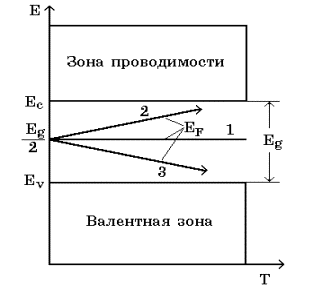Рис. 3.5. Положение уровня Ферми в собственном полупроводнике   1 - ; 2 - ; 3 - .

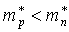Положение уровня Ферми в примесных полупроводниках может быть найдено из условия электронейтральности кристалла. Для донорного полупроводника это условие записывается в виде

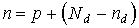, (3.24)

здесь N_d - концентрация донорных уровней, n_d - концентрация электронов на донорных уровнях. Концентрация электронов в зоне проводимости равна сумме концентраций дырок в валентной зоне и концентрации положительно заряженных ионов доноров (последняя, очевидно, равна N_d - n_d).

Концентрацию электронов на донорных уровнях можно вычислить, умножив концентрацию этих уровней N_d на функцию распределения Ферми-Дирака:

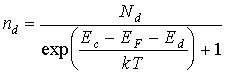, (3.25)

где Е_d - энергия активации донорных уровней.

Подстановка в условие электронейтральности (3.24) концентраций электронов (3.17) и дырок (3.19), а также концентрации электронов на донорных уровнях (3.25) приводит к следующему уравнению относительно положения уровня Ферми Е_F :

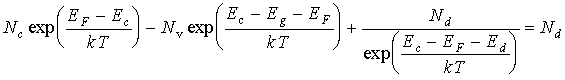. (3.26)

При подстановке концентрации электронов на донорных уровнях в уравнение (3.24 ) было сделано предположение, что газ электронов примесных атомов невырожденный, что позволило пренебречь единицей в знаменателе формулы (3.25).

Уравнение (3.26) ввиду его сложности обычно в общем виде не решают, а ограничиваются рассмотрением частных случаев. Например, при низких температурах, когда электроны в зоне проводимости появляются в основном за счет переходов с примесных уровней, а концентрация дырок близка к нулю, решение уравнения (3.26) имеет вид

. (3.27)

Из уравнения (3.27) следует, что при абсолютном нуле температуры энергия Ферми донорного полупроводника находится строго посередине между дном зоны проводимости и донорными уровнями. Температурная зависимость положения уровня Ферми определяется третьим членом в уравнении (3.27), который меняет знак с изменением температуры. Поэтому уровень Ферми с повышением температуры сначала смещается к зоне проводимости, а затем - к валентной зоне (рис. 3.6,а).

Аналогично можно получить выражение для температурной зависимости уровня Ферми в акцепторном полупроводнике. График этой зависимости схематически приведен на рис. 3.6,б.