Закон действующих масс. Невырожденный газ электронов и дырок

Вычислим концентрацию электронов в зоне проводимости полупроводника. Число электронов dN, находящихся в dZ состояниях энергетической зоны в соответствии с уравнением (3.1) определяется выражением

.

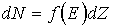Учитывая, что dZ = g(E) dE, получим

. (3.14)

Общее число электронов в зоне проводимости найдем, проинтегрировав выражение (3.14) в пределах зоны

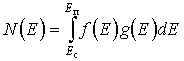, (3.15)

здесь Е_п - энергия потолка зоны проводимости. Поскольку функция распределения Ферми-Дирака очень быстро уменьшается с увеличением энергии, то верхний предел интегрирования можно взять равным бесконечности. Если степень заполнения энергетических состояний электронами в зоне проводимости мала (f(E) << 1), что практически всегда имеет место в полупроводниках, то единицей в знаменателе формулы (3.4) можно пренебречь. При этих условиях подстановка функций f(E) и g(E) в уравнение (3.15) приводит к следующему выражению для концентрации электронов в зоне проводимости:

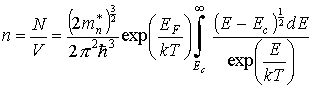. (3.16)

Преобразуем теперь выражение (3.16) к виду

.

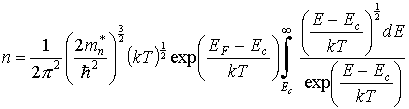Произведем замену переменных в подынтегральном выражении

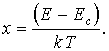
В результате получим

.

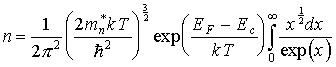Интеграл в этом выражении равен 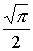. Следовательно

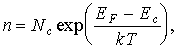(3.17)

где

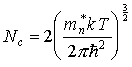. (3.18)

Величину N_c называют эффективной плотностью состояний в зоне проводимости. Это название связано с тем, что полная концентрация электронов, распределенных в действительности в определенном энергетическом интервале в зоне проводимости, такая же, как если бы зона была занята N_c уровнями, обладающими одной и той же энергией Е_c.

Аналогично можно вычислить концентрацию дырок в валентной зоне. Поскольку вакантное состояние в валентной зоне образуется в результате перехода электрона из этого состояния в зону проводимости, то вероятность того, что состояние с энергией Е в валентной зоне не занято, равна .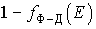

Тогда концентрация дырок

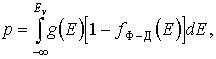
здесь E_v - потолок валентной зоны.

При условии, что газ дырок невырожденный, получим

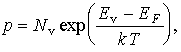(3.19)

где эффективная плотность состояний в валентной зоне

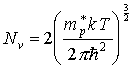. (3.20)

Перемножая выражения (3.17) и (3.19), получим

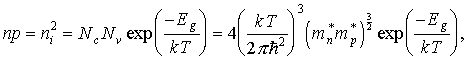(3.21)

где n_i - концентрация собственных носителей заряда в полупроводнике, E_g= E_c  E_v - ширина запрещенной зоны.

Соотношение (3.21) называется законом действующих масс. При выводе этого закона использовано предположение о том, что степень заполнения энергетических уровней носителями заряда много меньше единицы. Такой газ носителей называется невырожденным, а полупроводники - невырожденными.

В общем случае вырожденным газом в физике называется газ, свойства которого отличаются от свойств классического идеального газа вследствие квантово-механических свойств частиц газа. Вырожденный газ подчиняется квантово-механическим статистикам Ферми-Дирака или Бозе-Эйнштейна, невырожденный газ - статистике Маквелла-Больцмана. Условием перехода газа в невырожденное состояние является выполнение неравенства f(E) << 1. Можно показать, что это условие для электронного газа эквивалентно следующему соотношению:

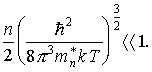(3.22)

Аналогичное соотношение справедливо и для дырок с заменой n на p и 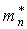на .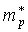

Вопрос о том, является газ носителей заряда в кристалле вырожденным или невырожденным определяется только его концентрацией и температурой. Подстановка численных значений величин, входящих в неравенство (3.22), приводит к выводу о том, что при комнатной температуре (Т ~ 300К) газ носителей будет невырожденным, если его концентрация значительно меньше 10²⁵ м^-3. Это условие выполняется практически для всех полупроводников. Поскольку концентрация электронов в зоне проводимости металлов превышает 10²⁸ м^-3, то электронный газ металлов всегда является вырожденным.

Таким образом, закон действующих масс выполняется для любого невырожденного полупроводника независимо от роли примесей, т.е. в любом невырожденном полупроводнике увеличение концентрации носителей одного знака приводит к уменьшению концентрации носителей противоположного знака. Следует отметить также, что произведение электронной и дырочной концентраций не зависит от положения уровня Ферми.