Интеграционная модель EOQ
Классическая модель EOQ Харриса-Уилсона позволяет определить оптимальный объем и периодичность размещения заказов на пополнения запасов для случая односкладских («изолированных») систем при условии детерминированного спроса.
Интеграционный подход при определении оптимального объема и периодичности размещения заказов на пополнения запасов в логистических системах заключается в следующем:
- оптимальная периодичность и объемы заказов сразу для звеньев системы рассчитываются таким образом, чтобы минимизировать совокупные затраты в системе в целом;
- осуществляется координация материального потока между уровнями системы в процессе осуществления поставок по времени и объему за счет формирования кратных партий отправок (см. рис. 11.9).
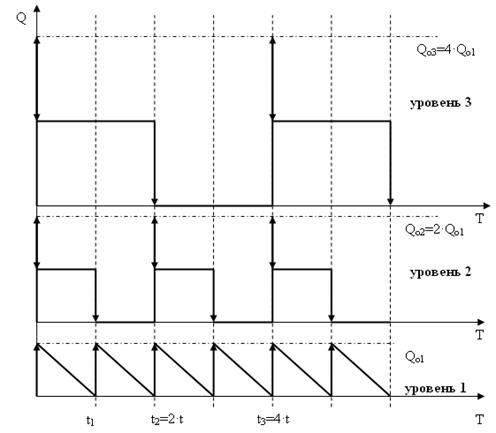
Qi – оптимальный размер заказа для i-ого уровня; ti – оптимальная периодичность поставок для i-ого уровня
Рис. 11.9. Координация материального потока на примере трехуровневой системы размещения запасов линейной конфигурации
Попытка учета взаимосвязи между отдельными звеньями при управлении запасами в логистических системах сделана в работе Свена Аксатера [48], где на примере двухуровневой системы размещения запасов линейной конфигурации (рис. 11.10) были получены зависимости для определения оптимальной величины заказа, которые в работах [48; 59] называются «эшелонированной моделью EOQ (multi echelon EOQ)».

Ai – затраты на заказ для пополнения запасов i-ого уровня; hi – затраты на содержание запаса i-ого уровня; d – плановая потребность (спрос) на готовую продукцию
Рис.11.10. Двухуровневая система запасов линейной конфигурации
Принцип работы эшелонированных моделей такой же, как и у классической модели оптимального размера заказа Харриса-Уилсона. Целевой функцией в моделях являются суммарные затраты, связанные с закупками и содержанием запасов. Искомые переменные – объемы заказов на пополнение запаса, при которых целевая функция минимизируется. Основное отличие эшелонированных моделей состоит в том, что рассматривается не одна, а несколько точек размещения запасов.
Основными условиями, определяющими возможность использования эшелонированных EOQ-моделей, являются следующие:
- детерминированная конечная потребность в материальных ресурсах (имеется в виду потребность в готовой продукции в сфере производства и / или распределения);
- постоянная и равномерно распределенная во времени интенсивность потребления у конечных потребителей;
- постоянное время выполнения заказа;
- фиксированные составляющие затрат на запасы.
В работе Свена Аксатера (Sven Axsäter) [48] основные расчетные формулы эшелонированной модели EOQ были получены с учетом следующих условий и ограничений:
1. Спрос на продукцию для уровня «1» детерминирован, равномерно распределен во времени и имеет постоянную интенсивность в течение всего рассматриваемого периода;
2. Затраты на заказ (Ai) и содержание запасов (hi) неизменны в течение всего рассматриваемого периода времени.
3. Продукция на уровнях «1» и «2» является неделимой и одной единице изделия на уровне «1» соответствует одна единица изделия на уровне «2».
4. Между объемами заказов для уровней «1» и «2» системы установлено отношение:
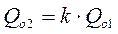 , (11.1)
, (11.1)
где k- некоторое целое положительное число (показатель кратности партий);
Qoi – оптимальный размер запаса на i-м уровне системы.
5. В системе предполагается возможность мгновенной поставки заказа: в случае поступления заказа от звена системы на уровне «1» в размере Qo1 часть запаса на уровне «2» в размере Qo1 может быть сразу же отгружена клиенту на уровне «1», см. рис. 11.11. Таким образом средний запас на уровне «2» за цикл будет:
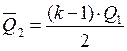 (11.2)
(11.2)
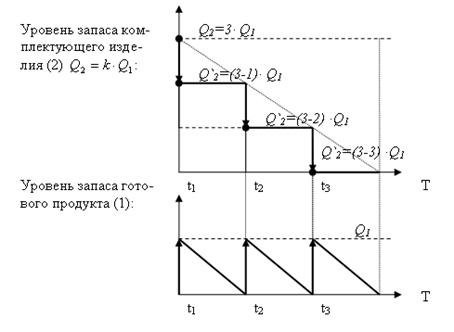
Рис. 11.11. Взаимосвязь уровней запасов изделий «1» и «2» при k = 3
Из рисунка 11.11 видно, что спрос на уровне «2» имеет ярко выраженный дискретный характер, что обусловлено координацией поставок на уровнях «1» и «2».
Рассмотрим порядок вывода расчетных формул эшелонированной модели EOQ с учетом описанных выше условий.
Затраты на заказ на уровне «1» составляют:
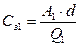 (11.3)
(11.3)
Затраты на хранение запаса на уровне «1»:
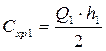 (11.4)
(11.4)
Учитывая то, что запасы на уровне «2» создаются исключительно для обеспечения потребления на уровне «1», а также принимая во внимание условия 3 и 5, затраты на заказ на уровне «2» можно представить следующим образом:
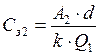 (11.5)
(11.5)
С учетом условия 6 затраты на хранение на уровне «2» составят:
 (11.6)
(11.6)
Таким образом суммарные затраты, связанные с запасами, в системе (рис. 11.10) составят:
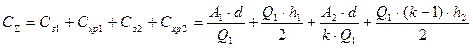 (11.7)
(11.7)
Функция суммарных затрат на запасы для случая двухуровневой системы линейной конфигурации (формула 11.7) – это выпуклая функция от двух переменных – Q1 и k. Поэтому для нахождения значения Q1 можновзять первую производную от выражения (11.7) по Q1, приравнять ее к 0 и выразить искомый параметр:
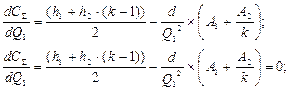 (11.8)
(11.8)
В результате получим выражение для расчета оптимального размера заказа на уровне «1» системы:
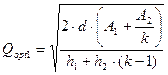 (11.9)
(11.9)
Подставив выражение (11.9) в формулу общих затрат (11.7) вместо Q1, получим выражение для расчета суммарных минимальных затрат:
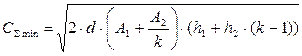 (11.10)
(11.10)
Для нахождения коэффициента k в работе возьмем производную 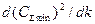 , приравняем ее к 0 и выразим искомый параметр [48]:
, приравняем ее к 0 и выразим искомый параметр [48]:
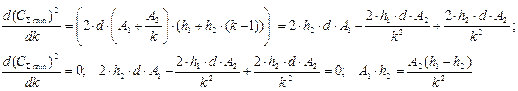 (11.11)
(11.11)
Таким образом получим выражение для расчета коэффициента k:
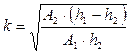 (11.12)
(11.12)
Поскольку k должно быть целочисленным, округление значения, полученного по формуле (11.12), осуществляют по следующему правилу [48]:
Если k`<1 (k`-это значение, найденное по формуле (24)), то k=1; если k`>1 и m≤ k`<m+1 (m – некоторое целое положительное число), то k=m при 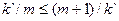 ; в противном случае k`=m+1.
; в противном случае k`=m+1.
Аналогично округление происходит и для значений Qopt I [48]:
Если m≤ Q`<m+1, где m – некоторое целое положительное число, то то Q=m при  ; в противном случае Q`=m+1.
; в противном случае Q`=m+1.
Оптимальный размер заказа на уровне «2» вычисляется по формуле (11.1), в которую подставляются найденные по формулам (11.12) и (11.9) значения k и Qopt1.
Пример 11.1:
Рассмотрим двухуровневую цепь поставок «оптовый склад» - «ритейлер». По данным ритейлера спрос на продукт «Х» составляет 40000 ед. в год. При этом затраты на размещение заказа для ритейлера составляют 100 у.е., а для оптовика – 200 у.е. Рассчитаем объемы оптимальных партий заказа для ритейлера и оптовика в 3-х случаях:
1. когда затраты на содержание запаса одинаковы для ритейлера и оптовика (h1=h2= 5 у.е.);
2. когда затраты на содержание запаса у оптовика выше, чем у ритейлера (5 у.е. и 2 у.е. за 1 продукции соответственно) - h1<h2;
3. когда затраты на содержание запаса у оптовика меньше, чем у ритейлера (2 у.е. и 5 у.е. за 1 продукции соответственно) - h1˃h2;
Прежде всего, по формуле (11.12) рассчитаем коэффициент k для каждого случая:
При h1=h2:
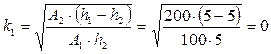
получается, что в этом случае запас на 2-м уровне (у оптовика) не хранится.
При h1<h2:
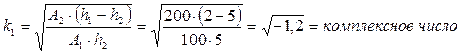
при таком соотношении определить коэффициент k с точки зрения математики вообще не возможно.
При h1˃h2 :
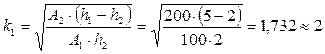
Следовательно, для варианта h1˃h2 можно рассчитать значения Qopt1 и Qopt2 по формулам (11.9) и (11.1) соответственно:
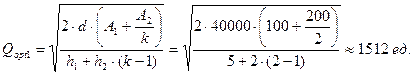
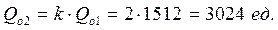
Рассчитаем также суммарные минимальные затраты (формула (11.10)):
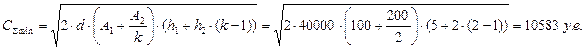
Как показали проведенные нами расчеты (см. пример 11.1), возможность применения зависимостей, предложенных Свеном Аксатером в работе [48], ограничена условием: h2< h1, то есть затраты на хранение на втором уровне (центральный склад) должны быть всегда ниже затрат на складах первого уровня (региональные склады). Данное утверждение базируется на том, что затраты на хранение традиционно определяются как процент от стоимости продукции, а стоимость продукции на региональных складах увеличивается за счет дополнительных затрат на транспортировку и грузообработку:
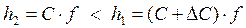 , (11.13)
, (11.13)
где С – цена продукции;
Δ С – добавленная стоимость;
f - процент от цены продукции, приходящийся на затраты по хранению.
В тоже время неравенство (11.13) не всегда справедливо, поскольку склады на разных уровнях логистических систем могут быть по-разному оснащены, система расчета тарифа на складские услуги может быть разной, что может привести к ситуации, когда h2≥ h1.
Анализ формулы (11.12) эшелонированной модели EOQ, рассматриваемой в работе [48], показывает, что:
- если h2> h1, то коэффициент k становится комплексным числом (при расчетах получается квадратный корень из отрицательного числа);
- если h2= h1, то коэффициент k = 0, и зависимость для Qo2 теряет смысл;
- если k≤1, то запас на 2-м уровне не хранится.
Чтобы преодолеть эти ограничения можно ввести дополнительное условие о том, что в случае поступления заказа от звена системы на уровне «1» в размере Qo1 часть запаса на уровне «2» в размере Qo1 не отгружается клиенту на уровне «1» сразу, а подлежит хранению в течение первого цикла. Таким образом для обозначения кратности объемов заказов используется уже множитель (k+1). В результате произойдет корректировка расчетных формул (см. табл. 11.2 – вариант ИНЖЭКОНа). Графически различие между двумя рассматриваемыми моделями показано на рис. 11.12.
Таблица 11.2
Параметры интеграционной модели EOQ для двухуровневого размещения запасов (Вариант ИНЖЭКОНа)
| Параметр | Расчетная формула |
| Оптимальный размер заказа для уровня «1» | 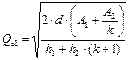
|
| Оптимальный размер заказа для уровня «2» | 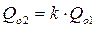
|
| Параметр кратности партий | 
|
| Суммарные минимальные затраты в системе | 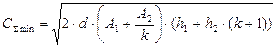
|
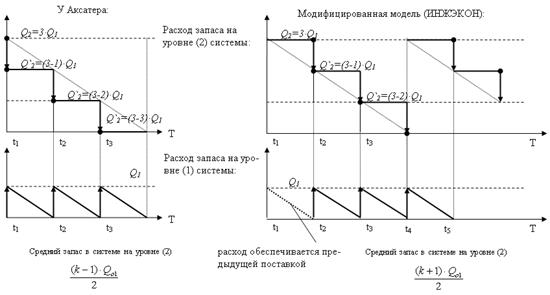
Рис. 11.12. Альтернативные подходы к описанию процесса расходования запасов
Пример 11.2:
Рассмотрим цепь поставок «оптовый склад» - «ритейлер» с теми же параметрами, что и в примере 11.1, но расчеты будем осуществлять уже с использованием формул из табл. 11.2 (вариант ИНЖЭКОНа).
рассчитаем коэффициент k для каждого случая:
при h1=h2:
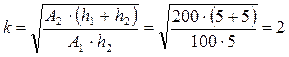
тогда

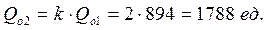
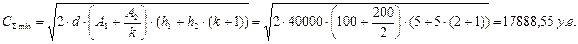
при h1<h2:
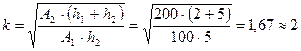
тогда
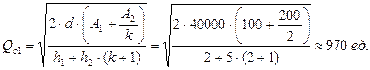
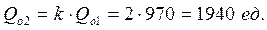
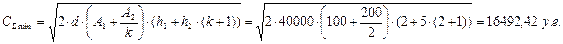 при h1˃h2 :
при h1˃h2 :
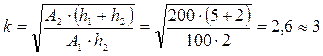
тогда
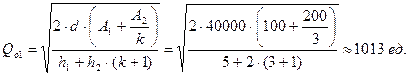


Проведенные нами расчеты показали, что для модели с (k+1) характерны следующие ограничения:
- если h1<h2 и A1=A2, либо A1<A2 менее чем в 2 раза, то k =1.
- практически всегда при h1<h2 и A1>A2 k =1.
Если проанализировать ограничения двух моделей (модели Аксатера и модели ИНЖЭКОНа), то можно сделать вывод о том, что модели дополняют друг-друга.
Также было установлено, что при больших значениях k (k≥3) результаты значений Qi и С∑, полученные с использованием моделей с (k-1) и (k+1) становятся очень близкими (см. рис. 11.13 и 11.14). Однако больших значений k можно добиться лишь при большой разнице в затратах на заказ и хранение между складами уровней «1» и «2», например, разница между затратами на хранение должна составлять 9 и более раз!
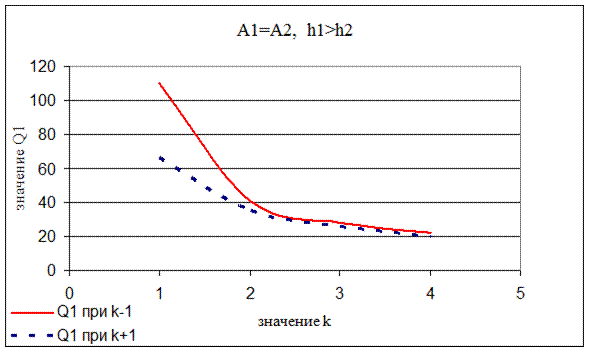
Рис. 11.13. Сходимость значений Q1 в моделях с (k-1) и (k+1) при различных значениях k
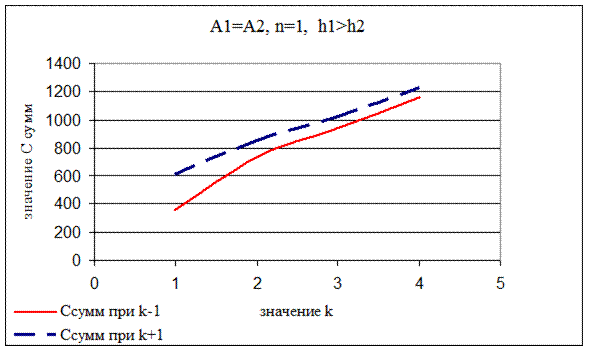
Рис. 11.14. Сходимость значений С∑ в моделях с (k-1) и (k+1) при различных значениях k
Для оценки эффекта от интеграции при управлении запасами в двухуровневой системе линейной конфигурации сопоставим расчеты расчетов по формулам из табл. 11.2 со случаем, когда решения в области управления запасами на уровне «1» и «2» не координировались (см. табл. 11.3).
Таблица 11.3
Случай независимого принятия решений в сфере управления запасами на уровнях «1» и «2» (нескоординированная модель)
| Параметр | Формулы для расчета |
| Оптимальный размер заказа для уровня «1» | 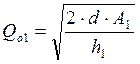
|
| Оптимальный размер заказа для уровня «2» | 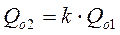
|
| Параметр кратности партий | 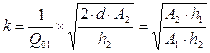
|
| Суммарные минимальные затраты в системе -C∑min для случая немгновенной отгрузки | 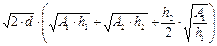
|
Суть нескоординированной модели заключается в следующем: звено системы на уровне «1» рассчитывает объем заказа на пополнение своего запаса по классической формуле Харриса-Уилсона, ориентируясь только на свои локальные затраты; звено на уровне «2» подстраивается под запросы, поступающие от звена на уровне «1», заказывая всегда объем запаса k·Qo1.
В таблице 11.4 приведены результаты расчетов параметров модели EOQ для случая двухуровневой системы размещения запасов линейной конфигурации при координированном и нескоординированном вариантах с использованием эшелонированной модели EOQ в формулировке ИНЖЭКОНа.
Таблица 11.4
Результаты вычислений для случая двухуровневой системы
| Дано | Вариант 1 | Вариант 2 |
| Спрос на продукцию (d) | ||
| Затраты на заказ для уровня «1» (A1) | ||
| Затраты на заказ для уровня «2» (A2) | ||
| Затраты на хранение для уровня «1» (h1) | ||
| Затраты на хранение для уровня «2» (h2) | ||
| Расчетные показатели при интегрированном управлении | ||
| Параметр кратности партий - k | ||
| Qopt1 | ||
| Qopt2 | ||
| C∑инт | ||
| Расчетные показатели при «изолированном» управлении | ||
| Q1 | ||
| Q2 | ||
| C∑изол | ||
| Экономический эффект по затратам | ||
| (C∑изол - C∑инт)/ C∑изол | 15,2% | 6,22% |
Проведенные нами вычисления показали, что эффект от интеграции может составлять от 6% до 15% в зависимости от соотношения затрат на хранение и заказ в системе.
В тоже время представляет интерес оценка того, как меняются индивидуальные значения затрат для уровней «1» и «2» в случае интегрированного и независимого принятия решений в сфере управления запасами. Результаты расчетов приведены в таблице 11.5.
Таблица 11.5
Значения затрат для уровней 1 и 2 в случае интегрированного и независимого принятия решений в сфере управления запасами
| Исходные данные | различные варианты сочетания затрат | ||||
| Спрос на продукцию (d) | |||||
| Затраты на заказ для уровня «1» (A1) | |||||
| Затраты на заказ для уровня «2» (A2) | |||||
| Затраты на хранение для уровня «1» (h1) | 4,5 | 3,3 | 3,3 | ||
| Затраты на хранение для уровня «2» (h2) | |||||
| C1 координ в модели с (k-1) | 259,46 | Не возможно | 317,88 | 296,82 | 370,90 |
| С1 некоординир в модели с (k-1) | 244,95 | 244,95 | 300,00 | 256,91 | 363,32 |
| C1 координ в модели с (k+1) | 249,75 | 360,50 | 318,52 | 269,49 | 382,00 |
| С1 некоординир в модели с (k+1) | 244,95 | 244,95 | 300,00 | 256,91 | 363,32 |
| C2 координ в модели с (k-1) | 86,96 | Не возможно | 106,38 | 148,15 | 74,07 |
| С2 некоординир в модели с (k-1) | 121,95 | 243,90 | 149,25 | 256,41 | 90,91 |
| C2 координ в модели с (k+1) | 350,25 | 888,50 | 317,88 | 431,94 | 365,00 |
| С2 некоординир в модели с (k+1) | 367,95 | 1227,90 | 350,25 | 490,41 | 420,91 |
Результаты расчетов (табл. 11.5) показывают, что в случае интегрированного управления запасами для двухуровневой системы линейной конфигурации суммарные затраты ниже, чем в случае нескоординированного принятия решений. Однако при координации происходит увеличение затрат для одного из звеньев по сравнению с нескоординированным вариантом; в нашем примере увеличение затрат произошло для звена первого уровня.
Результаты проведенных расчетов подтверждают логистический принцип «глобальной оптимизации», который подразумевает согласование локальных целей функционирования звеньев логистических систем и минимизацию совокупных издержек системы в противовес локальной оптимизации. Получается, что локальная оптимизация приводит к худшим результатам в плане затрат для системы в целом. При «глобальной оптимизации» совокупные издержки системы снижаются, но при этом могут увеличиться локальные затраты одного из звеньев. Последнее позволяет сделать вывод о том, что интегрированное управление запасами эффективно для случая корпоративных сетевых бизнес-структур в большей степени, чем для независимых компаний. В случае независимых компаний один из участников обязательно проиграет от интеграции, если, конечно, не будет предусмотрен механизм перераспределения эффекта, когда «выигравшая» от интеграции компания передает часть образовавшегося от экономии на издержках дохода в пользу «проигравшей» стороны.
Вопросы и задания для самостоятельной работы
1. Чем отличается логистический (интеграционный) подход к управлению запасами в цепях поставок от традиционного?
2. Для каких сфер бизнеса наиболее актуально применение интеграционного подхода к управлению запасами?
3. Что означает термин «многоуровневая система запасов»?
4. Какие типы структур многоуровневого размещения запасов в логистических системах существуют?
5. Что понимается под «элементом многоуровневой системы», и какие типы связей могут существовать между элементами многоуровневых систем?
6. В чем состоит сущность интеграционной (эшелонированной) модели EOQ?
7. Приведите основные формулы, используемые при расчете пара метров эшелонированных моделей EOQ.
8. Каковы основные условия, определяющие возможность использования эшелонированных моделей EOQ?
9. Как на примере использования интеграционных моделей EOQ подтверждается справедливость одного из основных принципов логистики – «принципа глобальной оптимизации»?
10. Для получения 45 кг сахара требуется порядка 290 кг сахарной свеклы (не считая вспомогательных компонентов). Необходимо определить оптимальные значения запасов для сырья – сахарной свеклы и готовой продукции – сахара, если известно следующее:
- предполагаемый объем выпуска сахара составляет 45000 кг;
- затраты на хранение 1 кг сахарной свеклы 0,05 у.е.
- затраты на хранение 1 кг сахара 0,2 у.е.
- затраты на заказ сахарной свеклы 50 у.е.
- затраты на заказ сахара 75 у.е.
При решении задачи необходимо учесть тот факт, что для изготовления 1 ед. готового изделия (уровень «1» системы запасов) требуется не 1, а n единиц сырья (уровень «2» системы).
12. УПРАВЛЕНИЕ ЗАПАСАМИ С УЧЕТОМ классификации материальных ресурсов: МЕТОДЫ АВС и XYZ
АВС-анализ
Метод АВС в теории управления запасами – «способ формирования и контроля за состоянием запасов, заключающийся в разбиении номенклатуры N реализуемых товарно-материальных ценностей на три неравномощных подмножества А, В и С на основании некоторого формального алгоритма». В основе метода лежит так называемое «правило Парето»: «внутри определенной группы или множества отдельные малые части обнаруживают намного большую значимость, чем это соответствует их относительному удельному весу в этой группе». Применительно к запасам на складах правило Парето выражается соотношением: на 20% общего количества номенклатуры приходится 80% стоимости хранимых запасов. В таблице 12.1 в хронологическом порядке приведены основе этапы формирования АВС-анализа.
Результаты АВС-анализа можно использовать с тем, чтобы определить периодичность контроля за состоянием запасов на складах предприятий, а также вероятность наличия страхового запаса (табл. 12.2).
Таблица 12.1
История возникновения и развития АВС-анализа [63 и др.]
| Дата | Событие |
| 1883 г. | Американский экономист Генри Джордж предложил проводить анализ размера фермерских хозяйств и собираемых налогов с использованием долей в общем объеме |
| 1894 г. | Джордж Шиллинг впервые подготовил статистический отчет, в котором были представлены статистические данные нарастающим итогом с указанием долей, занимаемых различными категориями. |
| 1905 г. | Макс Отто Лоренц в работе «Методы измерения концентрации благосостояния» привел графическое изображение числовых данных о концентрации экономических объектов (кумулята). Кривой Лоренца называют графическое построение, применяемое в настоящее время в ходе АВС-анализа. |
| 1906 г. | Вильфредо Парето высказал мнение, что 80 процентов благосостояния итальянского общества контролируется 20 процентами общественного капитала и сформулировал на основе этого свой знаменитый принцип, который лежит в основе эмпирического алгоритма АВС-анализа. |
| 1937 г. | Джозеф Джуран предложил использовать «принцип Парето» для изучения разнообразных экономических и общественных явлений. |
| 1948 г. | Генри Форд Дики из компании General Electric впервые употребил термин «АВС-анализ» на лекции для слушателей закрытого колледжа министерства обороны США. |
| 1951 г. | Генри Форд Дики опубликовал работу «Shoot for Dollars, not for Cents», в которой детально объяснил принципы применения введенного им аналитического инструмента для изучения товарной массы. |
| 1976 г. | В.С. Лукинский и Н.И. Веревкин предложили графический способ выделения групп А,В,С. |
| 1989 г. | Бенито Флорес и Клей Вайбак публикуют одну из первых работ, посвященных многокритериальному АВС-анализу. |
| 1997 г. | Группа исследователей под руководством В.С. Лукинского предложила аналитический метод выделения групп А,В,С. |
Таблица 12.2
Характеристика номенклатурных групп А, В и С [32]
| Группа | Периодичность контроля | Уровень обслуживания (вероятность отсутствия дефицита) | Тип оборудования; расположение продукции на складе | Методы прогнозирования, используемые при управлении запасами данной группы | Применяемые концепции логистики |
| А | ежедневный (непрерывный) | 0,95-0,99 | Гравитационные стеллажи; «горячая зона» | Комбинированные методы, специальные программы, имитационной моделирование | QR, VMI, JIT (JIT II), DTD, MRP и др. |
| В | одна-две недели | 0,9; 0,95-0,97 | Въездные стеллажи | Трендовые модели с учетом сезонности | JIT, DTD, MRP и др. |
| С | месяц, квартал и более | 0,8-0,9 | Клеточные стеллажи и мелкая комплектация, «холодная» зона | Простые модели (сглаживание и др.) | - |
Позиции номенклатуры, отнесенные к группе А – немногочисленные, но на них приходится преобладающая часть денежных средств, вложенных в запасы. Это особая группа с точки зрения определения величины заказа по каждой позиции номенклатуры, контроля текущего запаса, затрат на доставку и хранение.
К группе В относятся позиции номенклатуры, занимающие среднее положение в формировании запасов склада. По сравнению с позициями номенклатуры А, они требуют меньшего внимания, за ними производится обычный контроль текущего и страхового запасов на складе и своевременность заказа.
Группа С включает позиции номенклатуры, составляющие большую часть запасов: на них приходится незначительная часть финансовых средств, вложенных в запасы. Как правило, за позициями группы С не ведется постоянный учет, а проверка наличия осуществляется периодически (один раз в месяц, квартал или полугодие); расчеты оптимальной величины заказа и периода заказа не выполняются.
На сегодняшний день используется как минимум 3 способа разделения объектов на группы согласно выбранному критерию или критериям: эмпирический, аналитический и дифференциальный. Общий алгоритм АВС-анализа с применением различных методов выделения групп приведен на рис. 12.1.
Эмпирический методбазируется на гипотезе, что деление на группы можно выполнить по аналогии и поэтому границы групп выбираются по результатам ранее проведенных исследований (табл. 12.3). Согласно рис. 12.1. использование эмпирического метода предусматривает выполнение следующих операций:
1. Формируется база данных, содержащая необходимую для анализа информацию о номенклатурных группах (наименование, единицы измерения, номенклатурные номера, стоимость, объемы расхода/реализации в натуральном и денежном выражении, частота расхода и др.).
2. Выбирается критерий, по которому будет проводиться группировка номенклатурных позиций. В качестве критериев могут выступать различные показатели, в зависимости от цели проведения АВС-анализа (см. табл. 12.3).

Рис. 12.1. Методы определения номенклатурных групп АВС
Таблица 12.3
Выбор критерия для проведения АВС-анализа
| Критерии | Цель проведения анализа |
| - объем расхода в ед. - частота расхода, ед./сут.; - оборачиваемость. | - оптимизация размещения продукции на складе; - выявление неликвидов |
| - стоимость запасов в ден.ед.; - частота расхода. | - классификация продукции для повышения эффективности управления запасами и снабжением |
| - объем реализации в ден. ед. | - классификация продукции для повышения эффективности сбытовой деятельности |
3. Полученные значения показателей Ci располагаются в убывающей последовательности - от максимального к минимальному:
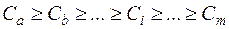 (12.1)
(12.1)
4. Затем производится присвоение новых индексов а=1, b=2,…, m=N, где N – общее количество наименований деталей номенклатуры, т.е.
 (12.2)
(12.2)
5. Для каждой позиции номенклатуры рассчитывается ее доля в общем объеме (в процентах) по выбранному ранее критерию:
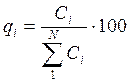 или
или 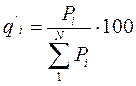 , (12.3)
, (12.3)
где P – условное обозначение критерия разделения на группы;
С – стоимостной критерий;
N – общее число классифицируемых объектов – позиций номенклатуры.
6. Величины qi (qi`) суммируются нарастающим итогом:
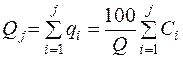 (12.4)
(12.4)
Интегральная (кумулятивная) зависимость Qj представляется в табличной форме в виде пар значений (Qj; i) или в виде графика (ось ординат Y – значения Qj, ось абсцисс – значения i).
По существу, эмпирический метод включает несколько вариантов.
Первый, наиболее распространенный вариант, предусматривает выбор координат YA и YA+B, например, YA=80% и YA+B=95 %.
Затем, с помощью интегральной зависимости Qj, формула (12.4), находятся значения XA* и XA+B* , позволяющие разделить позиции номенклатуры N на группы А и В.
Второй вариант предусматривает решение обратной задачи: по заданным (выбранным) значениям координат XA и XA+B определяются границы YA* и YA+B* и сравниваются с допустимыми значениями. В качестве эталонных значений могут быть выбраны XA = 20 % и XA+B=50 %.
Поскольку первый и второй варианты дают как правило разные величины координат Y и X и соответственно разные оценки групп А, В и С, то возможно использование третьего варианта, представляющего собой компромисс указанных двух вариантов.
Таблица 12.4
Процентные соотношения групп А, В, С [32]
| Источник | Группа А | Группа В | Группа С | |||
| YA | XA | YB | XB | YC | XC | |
| Б.А. Аникин, др. | 15-20 | 10-15 | 5-10 | 50-55 | ||
| APICS (рекомендуемые параметры)* | 50-70 | 10-20 | 10-30 | 60-70 | ||
| R.H. Ballou | 60,7 | 14,3 | 28,4 | 35,7 | 10,9 | |
| 49,44 | 11,1 | 42,94 | 38,9 | 7,42 | ||
| Д.Дж. Бауэрсокс, Д.Дж. Клосс | ||||||
| Гаврилов Д.А. | 17,5 | 2,5 | ||||
| А.М. Гаджинский, | ||||||
| Глухов В.В., | ||||||
| М. Кристофер | ||||||
| М.Р. Линдерс, Н. Харольд - запасы - закупки - пример | 70-80 71,1 | 10-15 19,4 | 10-20 19,5 | - 5-20 9,5 | - 70-80 71,1 | |
| О.В.Маликов ** | ||||||
| В.И. Сергеев | 75-80 | 10-15 | 15-20 | 20-25 | 5-10 | 60-70 |
| Д.Уотерс | ||||||
| J. Shapiro | ||||||
| Примечание: *APICS – American Production and Inventory Control Society; ** - Маликов О.Б. Деловая логистика.- СПб.: Политехника, 2003. |
Пример 12.1:
Рассмотрим применение эмпирического метода на основе данных табл. 12.5. Выберем первый вариант и зададимся значениями для точки А YА=80 % («правило Парето») и точки В YA+B = 95%. В табл. 12.5 нет значения Qj, соответствующего YА=80 %, поэтому выбираем Qj=4=78% или Qj=5=82%. Соответственно группу А составляет 4 позиции номенклатуры (XA = 20 %) или 5 позиций (XA = 25 %). Аналогично для определения В при YA+B = 95% находим Qj=10=94,5%, т.е. XA+B=50 % и Qj=11=95,5% (XA+B=55 %).
Таким образом, из полученных решений можно выбрать: группа А (78%, 4 позиции), группа В (26,5%, 6 позиций), группа С (5,5% позиций).
Таблица 12.5
Определение номенклатурных групп АВС. Исходные данные
для примеров
| Исходные данные | Результаты обработки | Группа | ||||||
| № п\п | ni, ед. | цi, руб/ед. | ci, руб. | № п\п | сj, руб. | qj,% | åqj, % | |
| А | ||||||||
| В | ||||||||
| 1,5 | 94,5 | |||||||
| 95,5 | С | |||||||
| 0,9 | 96,4 | |||||||
| 0,8 | 97,2 | |||||||
| 0,7 | 97,9 | |||||||
| 0,6 | 98,5 | |||||||
| 0,5 | 99,0 | |||||||
| 0,4 | 99,4 | |||||||
| 0,3 | 99,7 | |||||||
| 0,2 | 99,9 | |||||||
| 0,1 | ||||||||
| сумма |
Дифференциальный метод. В основу метода положены соотношения, опирающиеся на средние значения критерия разбиения на группы:
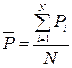 или
или 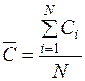 (12.5)
(12.5)
К группе А относят позиции номенклатуры, для которых выполняется соотношение:
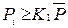 , (12.6)
, (12.6)
К группе В относят позиции номенклатуры, для которых выполняется соотношение:
 , (12.7)
, (12.7)
К группе С :
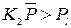 (12.8)
(12.8)
Величины коэффициентов ki в неравенствах (12.6) – (12.8) варьируются в интервалах: для k1 - от 2 до 6; для k2 - от 0,33 до 0,5, в зависимости от источника. Лицо принимающее решение вправе самостоятельно установить значение ki.
Пример 12.2:
Рассмотрим последовательность выбора номенклатурных групп дифференциальным методом при k1=6 и k2=0,5 по данным, приведенным в табл. 12.5. В качестве критерия берем показатель стоимости запасов, хранящихся на складе.
Поскольку среднее значение критерия:
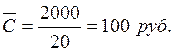 ,
,
то в группу А войдут позиции номенклатуры для которых величины Сi больше или равна 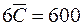 руб. Такой показатель только один, следовательно, величина YА=30 % и XA = 5 %. К группе В должны быть отнесены позиции номенклатуры, для которых Сi<600 руб. и
руб. Такой показатель только один, следовательно, величина YА=30 % и XA = 5 %. К группе В должны быть отнесены позиции номенклатуры, для которых Сi<600 руб. и  руб. Воспользовавшись таблицей, находим YA+B = 86%, XA+B=35 %, т.е. группа В составляет 56 % и в нее вошли 30% номенклатуры.
руб. Воспользовавшись таблицей, находим YA+B = 86%, XA+B=35 %, т.е. группа В составляет 56 % и в нее вошли 30% номенклатуры.
Несомненное достоинство дифференциального метода – простота: нет необходимости ранжировать показатели Сi и строить интегральную (накопленную) зависимость. Недостаток дифференциального метода – неопределенность выбора коэффициентов k1 и k2, приводящая в некоторых случаях к ошибочным результатам (в частности, невозможность выделения группы А).
Аналитический метод. Особенность данного метода состоит в том, что деление на группы А, В и С производится на основе определенного правила (критерия) и зависит от характера интегральной кривой (кумуляты) частоты показателя «P» - Qi . В настоящее время можно выделить два основных варианта (см. рис. 12.1) – графический и аналитический.
При графическом способе (рис. 12.2.) на оси ординат наносятся значения Qj, на оси абсцисс – индексы 1,2,…, N, соответствующие присвоенным номерам позиций номенклатуры. Точки с координатами (Qj ;i) на графике соединяются плавной кривой OO’D, которая в общем случае является выпуклой. Затем проводится касательная LM к интегральной кривой OO’D, параллельно прямой OD. Прямая OD соответствует равномерному распределению показателя 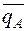 для всей номенклатуры:
для всей номенклатуры:
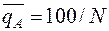 (12.9)
(12.9)
Абсцисса точки касания O’, округленная до ближайшего целого значения отделяет от всей номенклатуры первую группу NA (группа А), в которую входят позиции номенклатуры с показателями  . Таким образом, к группе А относятся все позиции номенклатуры, для которых значение показателя qi больше или равно среднему значению показателя для всей номенклатуры N.
. Таким образом, к группе А относятся все позиции номенклатуры, для которых значение показателя qi больше или равно среднему значению показателя для всей номенклатуры N.
Соответственно ордината точки (QA) указывает долю деталей группы А в процентах от величины общего показателя Qj.
Продолжим деление на группы оставшейся номенклатуры деталей, воспользовавшись вышеописанным приемом. Соединим точку O’ с точкой D и проведем касательную к кривой O’ O’’ D, параллельную прямой O’D. Абсцисса точки касания O’’ делит оставшуюся номенклатуру на группу В и группу С.

Рис. 12.2. Определение номенклатурных групп А, В, С
(графический способ)
Для оставшейся номенклатуры величина осредненного показателя составит:
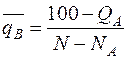 , (12.10)
, (12.10)
где NA - число позиций, вошедших в группу А.
Таким образом, в группу В попадают позиции номенклатуры с показателями qj, подчиняющимися неравенству:
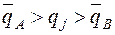 (12.11)
(12.11)
Следует указать, что если кривая OO’O’’D невыпуклая, то невозможно выделить ни одну из групп деталей; если кривая O’O’’D невыпуклая, то невозможно выделить группы В и С. Нетрудно заметить, что процедура деления может быть продолжена, если необходимо выделить еще одну или более групп.
Сопоставление графического и дифференциального подходов показывает их сходство при определении координат точки А (при k1=1) и расхождение, когда координата для определения группы В не строго фиксирована, а определяется кривизной интегральной зависимости и координатой точки А, т.е. k2≠const.
Пример 12.3:
 Рассмотрим вариант АВС анализа с использованием графического способа. На основе данных табл. 12.5 выделим группу А по правилу:
Рассмотрим вариант АВС анализа с использованием графического способа. На основе данных табл. 12.5 выделим группу А по правилу:
При N=20 и 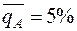 в группу А войдут NA=4 позиций номенклатуры, при этом YA=78,5 %, XA=20%.
в группу А войдут NA=4 позиций номенклатуры, при этом YA=78,5 %, XA=20%.
Для определения нижней границы группы В воспользуемся формулой (12.10). Подставив значения, получим:
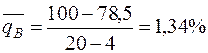
С учетом верхней ( 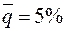 ) и нижней (
) и нижней ( 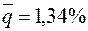 ) границ группы В находим: NB=6 ед., YA+B=94,5%, XA+B=50 %.
) границ группы В находим: NB=6 ед., YA+B=94,5%, XA+B=50 %.
Параметры группы С следующие: YC=5,5 %, XC=50%, т.е. 10 позиций номенклатуры.
При аналитическом способе последовательность этапов определения номенклатурных групп следующая:
1. Позиции номенклатуры N нормируются в интервале 0-1 и вводится аргумент X.
2. Выбирается аналитическая зависимость для аппроксимации интегральной кривой Qj:
y=f(x,ap) (12.12)
3. Определяются коэффициенты ap на основе систематизированных статистических данных с использованием метода наименьших квадратов (МНК) или численных методов.
При определении коэффициентов ар необходимо соблюдать начальные условия: первое – при x=0, y=0; второе при x=1, y=1. Это позволяет сократить число «нормальных» уравнений при использовании МНК. Например, для зависимости
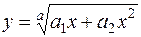 (12.13)
(12.13)
учет начальных условий приводит к соотношению a1=1-a2.
5. В качестве критерия деления на группы выберем условие, что в группу А попадут все позиции номенклатуры, показатели которых Сi больше или равны среднему значению показателя для всей выборки 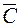 . Согласно теореме Лагранжа на выпуклой кривой f(x) существует одна точка А, касательная в которой параллельна хорде, в нашем случае линии, соединяющей начало координат (0,0) и точку с координатами (1,1). Для определения абсциссы точки А воспользуемся формулой:
. Согласно теореме Лагранжа на выпуклой кривой f(x) существует одна точка А, касательная в которой параллельна хорде, в нашем случае линии, соединяющей начало координат (0,0) и точку с координатами (1,1). Для определения абсциссы точки А воспользуемся формулой:
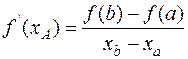 , (12.14)
, (12.14)
Где f1 (xA) – производная функции f(x) в точке касания А;
xа – искомая абсцисса точки касания;
f(xа), f(xв) – значения функции в начальной xА и конечной xВ точках.
С учетом начальных условий уравнение (12.14) запишется в виде: 

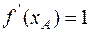 (12.15)
(12.15)
Решая уравнения (12.15), находим xА, затем координату yA=f(xA) и количество позиций номенклатуры, относящихся к группе А:
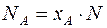 (12.16)
(12.16)
6. Для определения точки В, введем новую систему координат, принимая за начало отсчета абсциссу XA и ординату Y(XA). С учетом, что конечная точка имеет координаты XB=1, f(XB)=1, уравнение (12.14) записывается в виде:
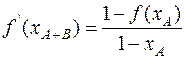 (12.17)
(12.17)
Дальнейшие вычисления аналогичны пункту 5: находим XA+B, затем YA+B и NA+B=(XA+B - XA)N.
Рассмотрим применение аналитического способа определения номенклатурных групп А, В и С.
Пример 12.4:
Допустим, что для расчетов выбрана функция вида:
 (12.18)
(12.18)
Анализ показал, что функция (11.15) может быть использована для аппроксимации Qj при значениях  . Если
. Если 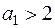 , то функция y(x) достигнет максимума в интервале 0-1, что противоречит характеру интегральной зависимости Qj.
, то функция y(x) достигнет максимума в интервале 0-1, что противоречит характеру интегральной зависимости Qj.
Примем 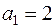 , тогда
, тогда 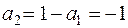 .
.
Для расчета абсциссы точки касания воспользуемся уравнением (12.13). Поскольку:
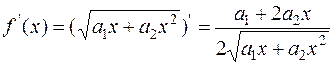 , (12.19)
, (12.19)
то после преобразований, находим
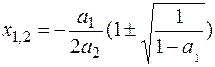 (12.20)
(12.20)
При подстановке значений a1 и a2 получим:
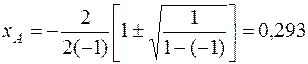
Второе значение xA=1,707отбрасываем.
Для определения yA подставим xA=0,293 в формулу (12.18) находим:
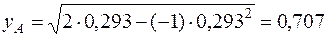
Таким образом, координаты xA и yA определяют границы группы А.
Определим координаты точки В. При подстановке f1(x) из формулы (12.19), и значений xA и yA в правую часть формулы (12.17) получим:
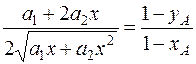
Обозначим:
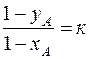
Тогда, после преобразований формула для определения абсциссы xA+B записывается в виде:
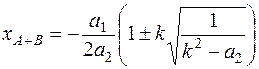 (12.21)
(12.21)
При 
находим координаты точки В: xA+B=0,618 и yA+B=0,924. Соответственно, параметры группы В: по номенклатуре 32,5%, по основному показателю – 21,7%.
XYZ - анализ
Анализ ХYZ подразумевает разделение всего ассортимента товаров (номенклатуры ресурсов) на три группы в зависимости от степени равномерности спроса или возможной степени точности прогнозирования.
Принципиальное отличие метода XYZ от метода АВС состоит в том, что анализируются количественные показатели, представленные, как правило, в виде динамического ряда qt для каждой i -той позиции номенклатуры.
К группе X относятся позиции номенклатуры, динамические ряды которых равномерны или незначительно колеблются (объемы реализации по которым практически неизменны во времени). Это позволяет осуществить прогноз с «высокой точностью» [29, 32 и др.].
К группе Y относятся позиции номенклатуры, у динамических рядов которых наблюдаются значительные колебания (объемы реализации по которым меняются во времени, но не очень значительно и/или достаточно предсказуемо), поэтому точность прогноза «ограничена» [29, 32 и др.].
Группа Z характеризуется нерегулярными (эпизодическими) отклонениями значений динамического ряда (объемы реализации по которым меняются во времени значительно и практически непредсказуемо), что не позволяет получить точные и достоверные прогнозные оценки [29, 32 и др.].
Деление на группы XYZ традиционно производится на основе статического коэффициента вариации:
 (12.22)
(12.22)
Входящие в формулу (12.22) величины среднего значения динамического ряда 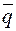 и среднего квадратического отклонения σ определяются по формулам (12.23) и (12.24) соответственно.
и среднего квадратического отклонения σ определяются по формулам (12.23) и (12.24) соответственно.
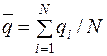 (12.23)
(12.23)
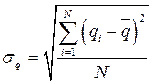 (12.24)
(12.24)
При значениях 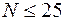 в формулу (12.24) рекомендуется подставить N-1.
в формулу (12.24) рекомендуется подставить N-1.
Процедура отнесения данной позиции номенклатуры к определенной группе сводится к сравнению статического коэффициента вариации νс вычисленного по формуле (12.22), с нормативными значениями νс, определяющими границы групп X,Y и Z, см. табл. 12.6.
Таблица 12.6
Интервальные границы групп X, Y, Z
| X | Y | Z | Источник |
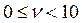
| 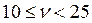
| 
| Аникин Б.А, Гаджинский А.М. |

| 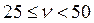
| 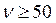
| Сергеев В.И. |
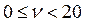
| 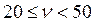
| 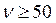
| Долгов А.П. Козлов В.К. Уваров С.А. |
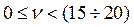
|
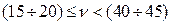
| 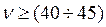
| Стерлигова А.Н. |
Пример 12.5:
В таблице 12.7 представлена информация об изменении спроса на товары А-J. Необходимо произвести XYZ-анализ номенклатуры.
Критерием классификации служит статический коэффициент вариации – νс, определяемый по формуле (12.22). Границы групп определяются по данным табл. 12.6. Результаты расчетов приведены в таблице 12.7.
Таблица 12.7
XYZ-анализ номенклатуры (классический подход)
| Период | Позиции номенклатуры | ||||||||||
| Год | Квартал | А | В | С | D | E | F | G | H | I | J |
| I | |||||||||||
| II | |||||||||||
| III | |||||||||||
| IV | |||||||||||
| I | |||||||||||
| II | |||||||||||
| III | |||||||||||
| IV | |||||||||||
| I | |||||||||||
| II | |||||||||||
| III | |||||||||||
| IV | |||||||||||
| Среднее | 319,2 | 319,17 | 319,2 | 365,19 | 184,3 | 82,99 | 203,4 | 118,4 | 406,2 | ||
| СКО | 16,63 | 16,629 | 16,63 | 90,49 | 46,77 | 58,39 | 31,6 | 97,15 | 42,16 | 72,32 | |
| К-т вар-ции,% | 5,2 | 5,21 | 5,2 | 25,4 | 15,2 | 38,1 | 47,8 | 35,6 | 17,8 | ||
| Группа (по Аникину и др.) | X | X | X | Y | Y | Y | Z | Z | Z | Y | |
| Группа (по Сергееву, Долгову и др.) | X | X | X | Y | Y | X | Y | Y | Y | X | |
| Группа (по Стерлиговой) | X | X | X | Y | Y | X | Y | Z | Y | X |
Дата добавления: 2016-01-07; просмотров: 2052;
