Усовершенствованный метод XYZ-анализа
В предыдущем разделе нами был рассмотрен классический подход к проведению XYZ. Основным недостатком классического подхода является недостаточно глубокая статистическая оценка динамических рядов. Расчет таких показателей как среднее, СКО и статический коэффициент вариации (νс) не позволяет в полной мере оценить динамику протекающих процессов, а, следовательно, не дает правильную оценку точности прогноза изучаемых параметров. Так, исходя из расчетов в табл. 12.7, продукты А, В и С имеют одинаковые значения среднего, СКО и коэффициента вариации, но при этом динамика процессов различна (см. рис. 12.3-12.5).
Как показывает рис. 12.3, спрос на продукт «А» подвержен сезонным колебаниям на фоне тенденции общего увеличения объемов потребления (тренд).
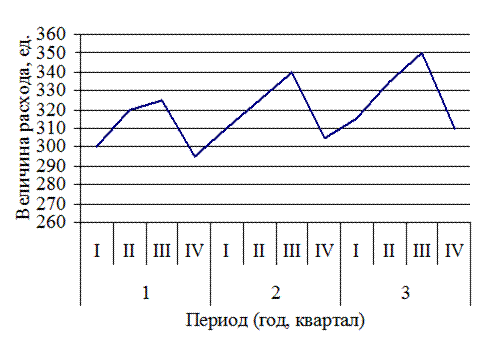
Рис. 12.3. Динамика расхода продукта «А»
Рис. 12.4 показывает, что потребность в продукте «В» прямо пропорциональна периоду времени и представляет собой практически линейную зависимость, без ярко выраженных сезонных и случайных колебаний.
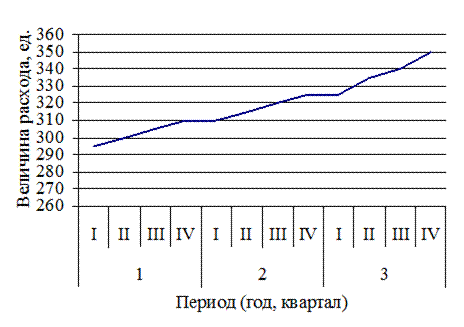
Рис. 12.4. Динамика расхода продукта «B»
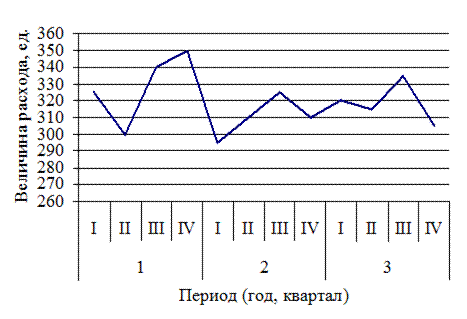
Рис. 12.5. Динамика расхода продукта «C»
Динамика расхода продукта «С», показанная на рис. 12.5, имеет более сложный характер. Спрос на продукт «С» сильно подвержен «случайным» колебаниям.
Если учитывать характер динамических рядов расхода, очевидным является то, что прогнозы потребности в продуктах «А», «В» и «С» будут иметь разную степень точности. Соответственно относить их к одной группе, как это сделано по результатам классического XYZ-анализа, нельзя.
Для того чтобы XYZ-анализ соответствовал возложенной на него задаче классификации номенклатуры запасов по степени прогнозируемости (а, значит, и управляемости), он должен основываться на более глубоком анализе временных рядов. Приведем основные этапы «усовершенствованного» XYZ-анализа.
Алгоритм усовершенствованного XYZ-анализа:
1. осуществляется оценка «крайних значений» исходных временных рядов;
2. подбирается уравнение тренда исходного временного рада;
3. определяются коэффициенты уравнения тренда;
4. определяются коэффициенты сезонности для уравнения тренда (при наличии сезонной волны);
5. оценивается ошибка прогноза по тренду для исходного временного ряда;
6. рассчитывается динамический коэффициент вариации;
7. по динамическому коэффициенту вариации определяется принадлежность рассматриваемой позиции номенклатуры к группам X, Y, Z.
Теперь рассмотрим каждый из этапов более подробно.
1. Осуществляется оценка «крайних значений» исходных временных рядов. Она необходима для выявления «экстремальных значений», которые являются случайными и «не типичными» для рассматриваемого ряда. Оценка крайних значений может проводиться методами Гроббса, Романовского, Ирвина и Арлея [34].
Наиболее удобным является метод Арлея, позволяющий определить наличие грубых ошибок как среди максимальных, так и минимальных значений. По методу Арлея определяется верхняя (xв) и нижняя (xн) границы интервала, в который попадают «типичные» значения рассматриваемого временного ряда:
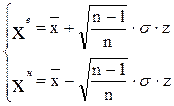 , (12.25)
, (12.25)
где 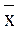 - среднее значение;
- среднее значение;
n – общее число значений временного ряда;
σ – СКО;
z – коэффициент Арлея, равный 1,98 для выборок, в которых n >9.
Значения динамического ряда, выходящие за верхнюю (xв) и нижнюю (xн) границы, отбрасываются.
2. Задаются видом тренда временного рада.
Модели трендов могут быть аддитивными и мультипликативными.
Аддитивная модель тренда:
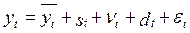 , (12.26)
, (12.26)
где yt – прогнозные значения временного ряда;
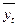 - среднее значение прогноза (тренд);
- среднее значение прогноза (тренд);
st – составляющая прогноза, отражающая периодические колебания, которые повторяются через примерно одинаковые промежутки в течение небольшого промежутка времени (сезонные колебания или сезонная волна);
vt – составляющая прогноза, отражающая периодические колебания, повторяющиеся в течение длительного промежутка времени (циклические колебания);
dt – составляющая, позволяющая учесть другие важные для конкретного прогноза;
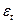 - случайная величина отклонения прогноза.
- случайная величина отклонения прогноза.
Мультипликативная модель тренда:
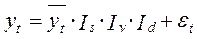 , (12.27)
, (12.27)
где yt – прогнозные значения временного ряда;
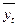 - среднее значение прогноза (тренд);
- среднее значение прогноза (тренд);
Is – коэффициент (индекс), учитывающий сезонные колебания;
Iv – коэффициент (индекс), учитывающий циклические колебания;
Id – коэффициент (индекс), учитывающий другие важные для конкретного прогноза факторы (фаза жизненного цикла, эффект от маркетинговых мероприятий и др.);
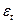 - случайная величина отклонения прогноза.
- случайная величина отклонения прогноза.
Тренд, сезонная, случайная и др. составляющие в аддитивной модели (тренд и случайная составляющая в мультипликативной модели) представляют собой функциональные зависимости (линейную, степенную, экспоненциальную, логарифмическую, синусоидную, косинусоидную и проч.), параметры которых могут быть найдены методом наименьших квадратов.
3. Определяют коэффициенты уравнения тренда;
4. Исследуют сезонные колебания и определяют (при наличии сезонной волны) коэффициенты сезонности для уравнения тренда, выбранного для аппроксимации;
5. Оценивают ошибку прогноза:
 , (12.28)
, (12.28)
где y*i – расчетные (теоретические) значения; yi – фактические значения; k – число степеней свободы, определяемое в зависимости от числа наблюдений (N) и числа оцениваемых параметров (z); k=N – z; для линейного тренда z=2.
6. Находят отношение ошибки прогноза к прогнозному значению – динамический коэффициент вариации:
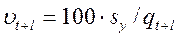 , (12.29)
, (12.29)
где 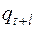 - прогнозное значение динамического ряда для периода t+l, рассчитанное с учетом тренда qt и сезонной составляющей;
- прогнозное значение динамического ряда для периода t+l, рассчитанное с учетом тренда qt и сезонной составляющей;
Sy - ошибка прогноза.
7. По динамическому коэффициенту вариации определяется принадлежность рассматриваемой позиции номенклатуры к группам X, Y, Z.
К группе X могут быть отнесены те позиции, для которых коэффициент вариации ≤ 0,1 (10%); к группе В –позиции, у которых коэффициент вариации находится в пределах 0,1<ν≤0,25; для позиций, относимых к группе Z коэффициент вариации ν > 0,25 [55].
Пример 12.6:
Пусть имеется ряд данных о потреблении некоторого продукта «D» за 4 года (см. табл. 12.7). Как показали проведенные ранее расчеты (табл. 12.7), статический коэффициент вариации для этого ряда = 0,25 и продукт «D» может быть отнесен к группе «Y».
Рассчитаем динамический коэффициент вариации (см. формулу 12.29). Для этого нам необходимо спрогнозировать значение расхода продукта «D» для ближайшего периода в будущем (например, 1-й квартал 5-ого года), а также оценить ошибку прогноза (формула 12.28).
Прежде чем начать прогнозирование проверим, все ли значения исходного ряда являются типичными для него. Для этого воспользуемся методом Арлея и рассчитаем верхнюю и нижнюю границы по формуле (12.25):
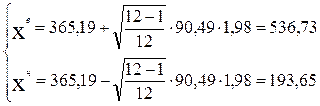
Таким образом, все значения, кроме значения для 1-ого квартала 1-ого года являются типичными для данного ряда по критерию Арлея. Нетипичное значение можно в дальнейшем не учитывать при прогнозировании.
На следующем этапе необходимо задаться моделью тренда. Для этого представим исходный динамический ряд (табл. 12.7 для «D») в виде графика «расход» - «время» - см. рис. 12.6 (предварительно убрав нетипичное значение).
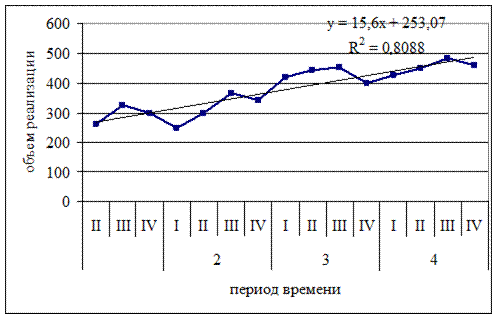
Рис. 12.6. Диаграмма «расход»-«время» для продукта «D»
Из рисунка 12.6 видно, что для процесса реализации товара «D» прослеживается линейный тренд с сезонными колебаниями.
Уравнение (модель) тренда можно подобрать, например, с помощью специальной функции табличного процессора Ms Excel. В нашем случае уравнение имеет вид:
y = 15,6x + 253,07 (12.30)
Чтобы учесть сезонность, воспользуемся мультипликативной моделью:
y = (15,6x + 253,07)·Is, (12.31)
где Is – индекс сезонности.
Индекс сезонности рассчитывается для каждого квартала каждого года по формуле:
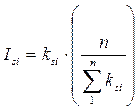 , (12.32)
, (12.32)
где – i число кварталов, i =1 ÷ n;
ksi – коэффициент сезонности для i-ого квартала, который рассчитывается по формуле:
 , (12.33)
, (12.33)
где – j число лет, j =1 ÷ m;
Yфij – фактическое значение расхода для i-ого квартала в j-м году;
Yтij –значение расхода для i-ого квартала в j-м году по тренду;
Прогнозные значения рассчитываются с использованием модели тренда, в которой учтена сезонность:
y = (15,6·t + 253,07)·Ist, (12.34)
где t – период времени.
Воспользовавшись выражением (12.34), определим (спрогнозируем) значение расхода товара «D» для первого квартала 5-ого года (t=17, 17-й период времени в табл. 12.8):
Y17 = (15,6·17 + 253,07)· 0,958 = 496,51 ед.
Результаты расчетов приведены в таблице 12.8
Таблица 12.8
| Год | Квартал | Период времени (t) | Размер реализации (Yфij) | Тренд | К-т сезонности (ksi) | Индекс сезонности (Isi) | Тренд + сезонность |
| I | - | - | - | - | - | ||
| II | 0,92 | 0,99 | 283,5 | ||||
| III | 1,08 | 1,08 | 325,6 | ||||
| IV | 0,94 | 0,95 | 302,3 | ||||
| I | 0,74 | 0,95 | 317,1 | ||||
| II | 0,85 | 0,99 | 345,8 | ||||
| III | 1,01 | 1,08 | 393,4 | ||||
| IV | 0,90 | 0,95 | 362,1 | ||||
| I | 1,06 | 0,95 | 376,9 | ||||
| II | 1,07 | 0,99 | 408,0 | ||||
| III | 1,06 | 1,08 | 461,2 | ||||
| IV | 0,90 | 0,95 | 421,9 | ||||
| I | 0,93 | 0,95 | 436,7 | ||||
| II | 0,95 | 0,99 | 470,3 | ||||
| III | 0,98 | 1,08 | 528,9 | ||||
| IV | 0,91 | 0,95 | 481,7 | ||||
| Прогноз | 0,95 | 496,5 |
Модель тренда с учетом сезонной составляющей, а также результаты прогнозирования в сопоставлении с исходным рядом расхода продукта «D» показаны на рис. 12.7.
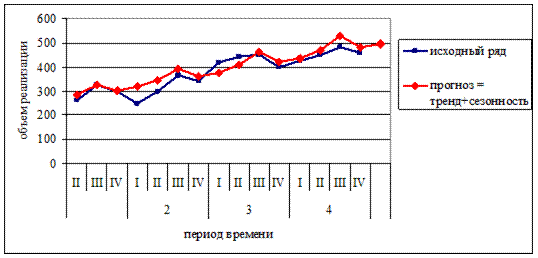
Рис. 12.7. Прогноз расхода продукта «D» с учетом сезонности
Теперь по формуле (12.28) рассчитаем ошибку прогноза (Sy), она составит 32,287.
Найдем отношение ошибки прогноза к прогнозному значению для периода t+1:
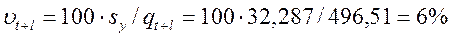
Получается, что товар «D» относится не к «Y» (этот результат дали проведенные ранее расчеты по «статической» технологии XYZ-анализа), а к «X».
Напомним, что к группе X относятся элементы номенклатуры, характеризующиеся стабильным спросом, незначительно колеблющимся около среднего значения. Прогноз будущей потребности в этих ресурсах может быть осуществлен с высокой степенью точности.
Потребность в материальных ресурсах, относимых к группе Y, характеризуется определенной тенденцией во времени (повышение или понижение), а также выраженными сезонными колебаниями. Для этих позиций получить точный прогноз уже сложнее.
Позиции номенклатуры, относимые к группе Z, потребляются не регулярно, либо спрос на них подвержен значительным колебаниям. Очень часто для этих позиций вообще не прослеживается очевидная зависимость спроса от времени. Прогноз по потребности в этих позициях осуществить очень сложно. Некоторые специалисты [55] рекомендуют осуществлять дополнительную разбивку группы Z на 2 подгруппы – Z1 и Z2. К группе Z1 можно отнести позиции, используемые более регулярно, для которых прослеживается хоть какая-то зависимость. К группе Z2 следует относить материальные ресурсы, потребляемые не регулярно.
Дата добавления: 2016-01-07; просмотров: 1448;
