Концепция простой логистической цепи
Одним из инструментов изучения роли посредников в процессе проектирования и оптимизации логистических систем, а также при управлении запасами в цепях поставок, является декомпозиция и представление логистических систем и цепей поставок в форме множества взаимосвязанных простых логистических цепей (ПЛЦ) [27, 28].
Под простой логистической цепью понимается часть логистической цепи (канала), включающей не менее двух основных звеньев логистической системы (ЗЛС) – «поставщика» и «потребителя», связанных между собой несколькими логистическими операциями: оформления заказа, транспортировки, хранения продукции и др. Расширение ПЛЦ возможно за счет основных посредников («третья сторона» в логистике): перевозчиков и складов общего пользования (грузовых терминалов).
Известно, что одной из основных аналитических зависимостей, отражающих интересы «трех сторон» в логистике (поставщика, потребителя, перевозчика и др.) является модель расчета оптимальной партии заказа Харриса-Уилсона (или EOQ, см. п. 5 настоящего пособия). Анализ данной модели показал, что она допускает различные интерпретации, поскольку основные элементы могут быть учтены различными способами в зависимости от следующих факторов:
- кто осуществляет перевозку и хранение (поставщик, потребитель или посредник);
- как рассчитываются затраты на хранение;
- как учитывается добавленная стоимость за транспортировку и организацию заказа в цене единицы продукции, поступившей на склад потребителя или посредника.
На рис.13.1 приведены несколько вариантов простых логистических цепей (A, B, C, D).
Вариант А включает только два звена: поставщика и потребителя, при этом не определено, кто осуществляет логистические функции (операции) оформления заказа, транспортировку и хранение.
Вариант В помимо поставщика и потребителя включает одного посредника (перевозчик).
Вариант С включает поставщика и потребителя, осуществляющего оформление заказа, а также двух посредников: перевозчика и склад, на котором потребитель хранит свою продукцию.
Вариант D отличается от других тем, что потребитель оформляет заказ и осуществляет перевозку, а при расчете затрат на хранение продукции на складе посредника не учитывается стоимость единицы продукции (аренда складских помещений).
Рассмотрим варианты взаимодействия и взаимовлияния элементов ПЛЦ, представляющие наибольший интерес.

Сп, Сп1 – цена единицы продукции; С0 – затраты на оформление заказа; Ст, Ст* - различные варианты затрат на транспортировку партии; Сх, Сх (ΔС) – различные варианты затрат на хранение продукции; ΔС – добавленная стоимость
Рис.13.1. Варианты представления затрат основных участников простой логистической цепи
В классической модели EOQ при определении суммарных затрат (ф. 5.2 и 5.5) не конкретизируется роль участников и не отражается характер распределения затрат между поставщиком, потребителем (и перевозчиком), а также не учитывается добавленная стоимость в цене продукции, появившуюся в результате выполнения.
В тоже время на выходе простого логистического звена цена единицы продукции СП1, отпускаемой со склада потребителя, который становится поставщиком в простом логистическом звене следующего (нижнего) уровня, должна учитываться с учетом добавленной стоимости ΔС, включающей затраты, связанных с выполнением логистических операций – оформление заказа, транспортировка и хранение на складе. Расчетная формула для СП1 может быть представлена в виде:
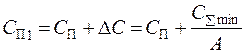 (13.1)
(13.1)
Пример 13.1:
Рассчитаем показатели модели EOQ для простейшего варианта логистической цепи (вариант А, рис. 13.1) при следующих исходных данных: А=2000 ед., СП=10 руб., Со=50 руб.; СТ=200 руб.; f=0,25. При подстановке в формулы (5.6) – (5.9) находим:
- оптимальная величина заказа So=632 ед.;
- минимальные суммарные затраты С∑min=1581 руб.;
- цена единицы продукции (при получении со склада потребителя с учетом затрат на заказ, транспортировку и хранение) СП1=10,79 руб.
Таким образом, добавленная стоимость единицы продукции составила ΔС=0,79 руб./ед.
Рассчитаем также для данного варианта число заказов:
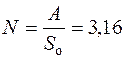 ,
,
периодичность заказов:
 дн.,
дн.,
затраты на оформление заказов (в год):
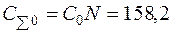 руб.
руб.
затраты на транспортировку С∑Т и хранение С∑х:
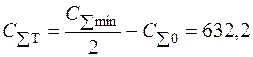 руб.
руб.
 руб.
руб.
Возможная интерпретация классического варианта данной ПЛЦ соответствует, на наш взгляд, известной логистической концепции VMI (Vendor Managed Inventory), согласно которой поставщик или посредник берет на себя обязательство пополнять запасы потребителя и поддерживать их на необходимом уровне.
В качестве альтернативного варианта рассмотрим случай, когда посредник (или поставщик) выполняет транспортировку, а оценка затрат на хранение продукции на складе потребителя включает добавленную стоимость за перевозку каждой единицы продукции (см. рис.13.1, вариант В).
В общем случае данный вариант может быть представлен в виде системы
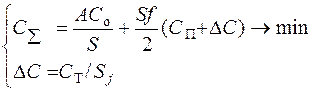 (13.2)
(13.2)
Особенность системы (13. 2) состоит в том, что при записи в виде двух уравнение удается отразить динамику (разновременность) протекания процессов, их последовательное выполнение, а именно: заказ – транспортировка - хранение. Решение системы (13. 2) предполагает, что для нахождения оптимальной величины заказа So (из первого уравнения) необходимо знать ΔС. В свою очередь, входящее во второе уравнение ΔС зависит от Sj= So, т.е. оптимальной партии поставки определяемой из первого уравнения.
С учетом указанных особенностей выражение для суммарных затрат запишем в виде:
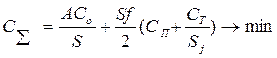 (13. 3)
(13. 3)
Для определения S можно воспользоваться двумя способами: численным и итерационным.
Итерационная формула для определения величины EOQ записывается в виде:
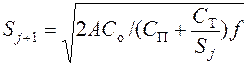 ( 13.4)
( 13.4)
Подставляя в правую часть Sj=So , находим первое приближение S1 и сравниваем с So, затем подставляем Sj= S1 и находим S2 и т.д. Процесс повторяется несколько раз до достижения заданной точности величины оптимальной партии Soj.
Соответственно минимальные суммарные затраты и цена единицы продукции с учетом добавленной стоимости равны:
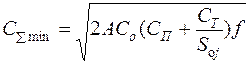 (13.5)
(13.5)
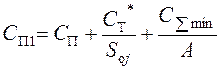 , (13.6)
, (13.6)
где Soj – оптимальная величина EOQ, рассчитанная по формуле (13.4).
В таблице 13.2 приведены результаты расчета So на основе исходных данных предыдущего примера, кроме одного параметра: затраты на транспортировку одного заказа у посредника (перевозчика) Ст*=175 руб./заказ.
Таблица 13.2
Результаты расчета минимальных затрат модели EOQ
(численный способ)
| Sj, ед. | 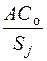 , руб. , руб.
| 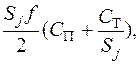 руб. руб.
| C∑, руб. |
| 500,0 | 271,9 | 771,9 | |
| 444,4 | 303,1 | 747,5 | |
| 400,0 | 334,4 | 734,4 | |
| 363,6 | 365,6 | 729,2 | |
| 333,3 | 396,9 | 730,2 | |
| 307,7 | 428,1 | 735,8 |
Из таблицы 13.2 видно, что минимальная величина общих затрат составляет около С∑=729,2 руб. при Sj=275 ед. продукции.
Рассмотрим теперь вариант ПЛЦ, в котором потребитель оформляет заказ, перевозка осуществляется посредником, а расчет затрат на хранение на складе потребителя (или посредника) производится в зависимости от арендной платы за м2 (или м3) площади или объема (см. рис. 13.1, вариант С). В этом случае не требуется знания цены продукции и добавленной стоимости от предыдущих логистических операций. Согласно работе [27] уравнения суммарных затрат записывается в виде:
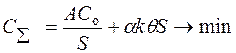 , (13.7)
, (13.7)
затраты на транспортировку (в год) будут равны:
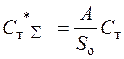 , (13.8)
, (13.8)
где a - затраты на хранение продукции в единицу времени с учетом занимаемой площади (объема) склада, руб.\м2 .ед. времени (руб.\м3 . ед. времени);
k - коэффициент, учитывающий пространственные габариты единицы продукции, м2\шт. (м3\шт.).
θ – коэффициент, учитывающий неодновременность поступления различных видов продукции на склад, 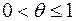 (примем θ=1) [27].
(примем θ=1) [27].
Определим оптимальный размер заказа с использованием стандартной процедуры оптимизации. После необходимых преобразований находим:
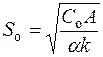 (13.9)
(13.9)
Величина минимальных затрат рассчитывается по формуле:
 (13.10)
(13.10)
Рассчитаем показатели модели EOQ для данного типа ПЛЦ с учетом, что Ст*=175 руб./заказ и α·k=2,5 руб./ед.год. При подстановке исходных данных находим:
 ед.
ед.
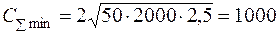 руб.
руб.
Поскольку затраты на транспортировку (в год) равны:
 руб.,
руб.,
то общие минимальные затраты:
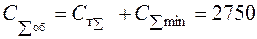 руб.
руб.
а цена продукции:
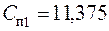 руб.
руб.
Рассмотрим теперь вариант D (рис. 13.1). В этом случае все затраты по оформлению заказа и транспортировке несет потребитель, но для хранения привлекается склад посредника, при этом в цене товара, поступающего на склад, учитывается добавленная стоимость за выполнение заказа (оформление и транспортировка). Система уравнений для суммарных затрат и добавленной стоимости записывается в виде:
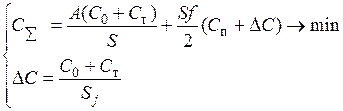 (13.11)
(13.11)
После преобразований находим итерационную формулу для EOQ:
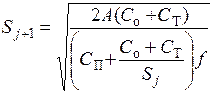 (13.12)
(13.12)
Расчет минимальных затрат производится по формуле:
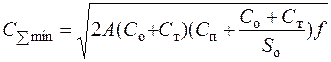 (13.13)
(13.13)
Анализ простых логистических цепей с учетом рассмотренных вариантов показал, что для дальнейших оптимизационных расчетов целесообразно остановиться на восьми типах ПЛЦ, приведенных в табл. 13.3.
Соответствующие зависимости для расчета оптимальной величины заказа So (Soj), минимальных суммарных затрат С∑min и общих минимальных затрат С∑об для каждого типа ПЛЦ даны в табл.13.4.
Результаты расчетов показателей для различных вариантов простой логистической цепи ПЛЦ (см. табл. 13.3 и 13.4), включающие величину оптимальной партии So (Soj), количество поставок, все виды затрат и цену продукции с учетом добавленной стоимости от выполнения логистических функций (операций), приведены в табл.13.5.
Таблица 13.3
Варианты организации взаимоотношений между участниками ПЛЦ и учета добавленной стоимости в цене продукции [27]
| Вариант ПЛЦ | Уравнения суммарных затрат С∑ и затрат на транспортировку | Комментарии |
 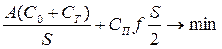
| Классическая модель EOQ (без конкретизации участников и учета добавленной стоимости). Возможно, что заказ, транспортировку и хранение совершает потребитель либо посредник. | |
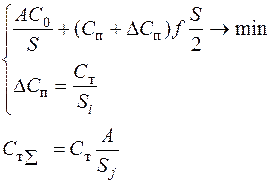
| Оформление заказа - потребитель; перевозка – посредник; при хранении (потребитель) в цене продукции учтена добавленная стоимость за транспортировку. | |
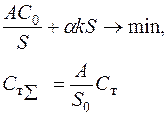
| Оформление заказа - потребитель; перевозка - посредник; при хранении добавленная стоимость не учитывается | |
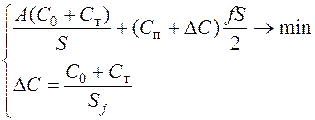
| Оформление заказа и транспортировка - потребитель; хранение – посредник; при хранении учитывается добавленная стоимость (оформление и транспортировка) | |
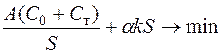
| Оформление заказа, транспортировка и хранение – потребитель (или VIM); добавленная стоимость не учитывается |
Окончание табл. 13.3
| Вариант ПЛЦ | Уравнения суммарных затрат С∑ и затрат на транспортировку | Комментарии | |
| 6* | 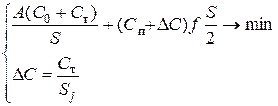
| Оформление заказа и транспортировка - получатель; хранение с учетом добавленной стоимости в цене продукта (только транспортировка) | |
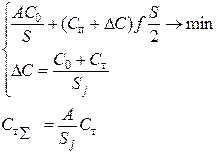
| Оформление заказа – получатель; транспортировка – посредник; посредник – хранение с учетом добавленной стоимости за оформление и транспортировку. | ||
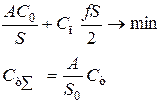
| Оформление заказа – получатель; транспортировка – посредник; хранение – получатель (или посредник) без учета добавленной стоимости при транспортировке. | ||
| * дискуссионный тип ПЛЦ, предусматривающий наличие хозрасчетных отношений внутри ЗЛС, например, со складом. | |||
Таблица 13.4
Расчетные зависимости для определения параметров простой логистической цепи [27]
| Варианты ПЛЦ | Оптимальная величина заказа S0, ед. | Минимальные затраты С∑min | Общие мимальные затраты С∑об |
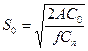
| 
| 
| |
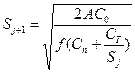
| 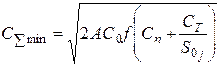
| 
| |
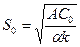
| 
| 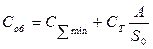
|
Окончание табл. 13.4
| Варианты ПЛЦ | Оптимальная величина заказа S0, ед. | Минимальные затраты С∑min | Общие мимальные затраты С∑об |
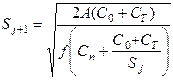
| 
| 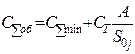
| |
 
| 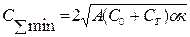
| 
| |
 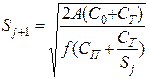
| 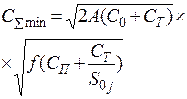
|
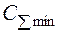
| |
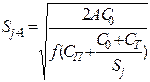
| 
| 
| |
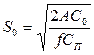
| 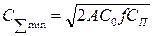
| 
|
Таблица 13.5
Результаты расчета показателей для различных вариантов ПЛЦ [27]
| Вариант (тип ПЛЦ) | Показатель | |||||||
| So | N | CΣmin | C∑0 | Cx(Cx*) | Cт∑(Ст∑*) | C∑об | Cп1 | |
| 3,16 | 158,2 | 790,5 | 632,3 | 10,790 | ||||
| 7,3 | 729,3 | (1277,5) | 2006,8 | 11,004 | ||||
| (1750) | 11,375 | |||||||
| 3,2 | 10,806 | |||||||
| 4,47 | 223,5 | 894,5 | 11,118 | |||||
| 3,22 | 161,3 | 803,2 | 642,4 | 10,803 | ||||
| 7,36 | 735,6 | 367,8 | (367,8) | (1287) | 2022,6 | 11,101 | ||
| 7,09 | 353,5 | 10,974 | ||||||
| Примечание: Ст*- затраты посредника (перевозчика) на транспортировку в год. Cx*- хранение на складе посредника. |
Из анализа таблицы 13.5 следует, что для рассматриваемого примера: при различных вариантах взаимодействия звеньев ЛС в простых логистических цепях размах значений цены единицы продукции на «выходе» ПЛЦ составляет от 10,79 руб. до 11,375 руб., т.е. около 5,4%; общие минимальные логистические издержки колеблются в широких пределах: от 1581 руб. до 2750 руб.
Попытаемся применить концепцию простой логистической цепи для оптимизации затрат логистической цепи, состоящую из 3-х ПЛЦ, см. рис.13.2.

Сп,,Сп1,Сп2 – цена единицы продукции на входе (выходе) ПЛЦ; С0 – затраты на оформление заказа; Ст, Ст*- различные варианты затрат на транспортировку партии; Сх, Сх (ΔС) – различные варианты затрат на хранение продукции; ΔС – добавленная стоимость
Рис.13.2. Логистическая цепь «центральный склад – региональный центр – магазины», включающая три ПЛЦ [27]
Логистическая цепь на рис. 13.2 выбрана нами в качестве примера не случайно. Такая схема ЛЦ, состоящая из 3-х звеньев, характерна для более 50% случаев дистрибьюции продукции, поэтому данный пример может быть интересен с практической точки зрения.
Из рисунка 13.2 видно, что ПЛЦ-1 включает поставщика (центральный склад) и потребителя первого уровня (региональный склад); для ПЛЦ-2 региональный склад становится поставщиком для потребителя второго уровня (магазин №1); для ПЛЦ-3 региональный склад становится поставщиком для потребителя второго уровня (магазин №2). Также в рассматриваемой цепи поставок предполагается, что транспортировка и хранение продукции могут осуществляться посредниками.
Пример 13.2:
В табл. 13.6 приведены исходные данные для логистической цепи, показанной на рис. 13.2. Далее в табл. 13.7 и 13.8 приведены результаты расчетов параметров модели EOQ для каждого 2-х звеньев рассматриваемой логистической системы, исходя из 8 возможных вариантов учета затрат на логистические операции в простых логистических цепях (см. табл. 13.3 и 13.4) Результаты расчетов в соответствии с разработанным подходом приведены в табл.2.9, 2.10.
Таблица 13.6
Исходные данные для расчета показателей модели EOQ [27]
| Наименование параметра | ПЛЦ-01 | ПЛЦ-11 | ПЛЦ-12 |
| 1. Потребность в заказываемом продукте, ед. | |||
| 2. Затраты на оформление заказа, руб./заказ |
Окончание табл. 13.6
| Наименование параметра | ПЛЦ-1 | ПЛЦ-2 | ПЛЦ-3 |
| 3. Транспортные затраты, руб./перевозка - потребитель Ст - посредник (перевозчик) Ст* | |||
| 4. Доля затрат на хранение от цены единицы продукции - потребитель - посредник | 0,25 0,25 | 0,20 0,15 | 0,20 0,20 |
| 5. Затраты на хранение единицы продукции αк | 2,5 | 2,0 | 1,0 |
| 6. Цена единицы продукции на входе (выходе) в ПЛЦ, Спi, руб. | 10,8* | 10,8* | |
| Примечание: * - приняты по результатам расчета для ПЛЦ-1 |
Таблица 13.7
Результаты расчетов показателей для ПЛЦ-2 [27]
| Вариант ПЛЦ | Показатели | |||||||
| S0 | N | C∑min | C0∑ | Cх (Сх*) | Ст∑ (Ст∑*) | С∑об | Сп11 | |
| 2,08 | 623,6 | 103,8 | 311,8 | 623,6 | 11,84 | |||
| 3,68 | 368,0 | 184,0 | 184,0 | (294,3) | 662,4 | 11,903 | ||
| 5,47 | (438) | 12,44 | ||||||
| 1,84 | 92,3 | (276) | 183,4 | 11,72 | ||||
| 3,15 | 948,6 | 474,3 | 316,3 | 948,6 | 12,38 | |||
| 2,11 | 633,6 | 105,8 | 211,2 | 316,8 | 633,6 | 11,86 | ||
| 3,22 | 312,6 | 160,8 | (160,8) | (257,2) | 11,75 | |||
| 3,59 | 287,4 | 647,4 | 11,87 | |||||
| Примечание: Ст* - см. табл. 13.6 |
Таблица 13.8
Результаты расчетов для ПЛЦ-3 [27]
| Вариант ПЛЦ | Показатели | |||||||
| S0 | N | C∑min | C0∑ | Cхр | Ст∑ (Ст∑*) | С∑об | Сп12 | |
| 2,08 | 727,5 | 623,5 | 11,84 | |||||
| 5,7 | 12,02 | |||||||
| 5,29 | 264,6 | 264,6 | 11,93 |
Окончание табл. 13.8
| Вариант ПЛЦ | Показатели | |||||||
| S0 | N | C∑min | C0∑ | Cхр | Ст∑ (Ст∑*) | С∑об | Сп12 | |
| 2,13 | (745) | 11,86 | ||||||
| 11,8 | ||||||||
| 2,93 | 106,5 | 635,5 | 11,86 | |||||
| 5,75 | 575,2 | 287,6 | (287,6) | 12,03 | ||||
| 5,49 | 11,97 | |||||||
| Примечание: Ст* -см. табл. 13.6 |
Из табл.13.7, 13.8 следует, что для ПЛЦ-2 с точки зрения общих минимальных затрат следует выбрать четвертый тип (С∑об=551 руб.) организации взаимоотношений между участниками, для ПЛЦ-3 - соответственно пятый тип (С∑об=1400 руб.). Таким образом, для приведенной на рис.13.2 логистической цепи, включающей три ПЛЦ, оптимальный вариант организации взаимоотношений между участниками будет выглядеть следующим образом:
- для ПЛЦ-1 все логистические функции (операции) по оформлению заказа, транспортировке и хранению осуществляет региональный центр или самостоятельная компания (посредник);
- для ПЛЦ-2 оформление заказа и транспортировку от распределительного центра осуществляет магазин №1, хранение производится на складе посредника (при этом в затратах на хранение учитывается добавленная стоимость за оформление и транспортировку);
- для ПЛЦ-3 все логистические функции (операции) осуществляются получателем (магазин №2) или компанией посредником, добавленная стоимость в цене товара не учитывается, т.к. хранение производится на условиях аренды складских помещений.
Результаты проведенных расчетов позволяют сформулировать критерий управления запасами в цепях поставок в виде:
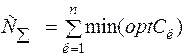 , (13.14)
, (13.14)
где Ск – к-я простая логистическая цепь (между i и i+1 ЗЛС).
Для рассматриваемого примера (Пример 2.1) минимальные общие затраты составят:
С∑=1581+551+1400=3532 руб.
Вопросы и задания для самостоятельной работы
1. Назовите основные 3 группы посредников в цепях поставок, приведите примеры.
2. Каковы функции посредников в цепях поставок (общий перечень)?
3. Что такое «аутсорсинг в цепях поставок»?
4. Какова технология аутсорсинга при управлении запасами?
5. В чем заключается сущность технологии VMI как альтернативы аутсорсингу при управлении запасами?
6. Назовите основные преимущества и недостатки аутсорсинга при управлении запасами в цепях поставок.
7. Что такое «простая логистическая цепь»?
8. Каковы возможные варианты организации взаимоотношений (распределения ответственности и учета добавленной стоимости за услуги при расчете затрат) между элементами простой логистической цепи (8 основных вариантов)?
9. Что дает использование концепции простой логистической цепи при управлении запасами или при проектировании логистических систем?
10. Какой критерий оптимизации при управлении запасами в цепях поставок следует использовать с точки зрения концепции простой логистической цепи?
Дата добавления: 2016-01-07; просмотров: 2419;
