Учет скидок в модели EOQ
При покупке партий товара большинство фирм дает скидки, величина которых зависит от размера партии (S). Среди различного вида скидок в управлении запасами наиболее часто используется так называемые оптовые скидки. Применение оптовых скидок означает, что цена единицы продукции Спj зависит от объема закупаемой партии Sj, при этом соблюдается правило, чем больше Sj, тем меньше цена Спj. Уменьшение цены представляется, как правило, в виде дискретной зависимости (см. рис. 5.2). На рис.5.2 показана ситуация, когда при величине заказа Sj≤100 ед. цена единицы товара Спо=400 руб.; при величине заказа S от 100 до 500 ед. цена единицы товара Сп1=350 руб.; наконец, при S больше 500 ед. цена Сп2=300 руб. Следовательно, заказывая 300 ед.продукции затраты на приобретение составят Ск=300х350=105 тыс. руб., а при заказе 600 ед. затраты Ск=180 тыс. руб.
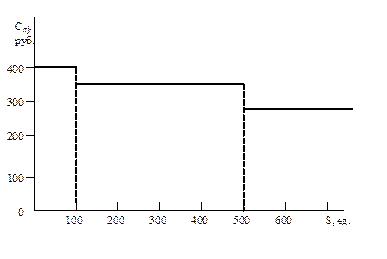
Рис. 5.2. Зависимость оптовой цены продукции (Cпj) от
объема заказа (S)
Иногда могут предоставляться дифференциальные скидки, при использовании которых скидки для каждой партии товара учитываются раздельно в каждом ценовом диапазоне. Здесь используется следующее правило. Если размер заказа колеблется от 1 до S1, например до 100 ед., то цена единицы изделия составляет Спо (допустим Спо=400 руб.); при размере заказа от S1+1 до S2 (от 101 до 500 ед.) цена снижается до Сп1 (Сп1=350 руб. как при оптовой скидке) и т.д. Но при дифференциальной скидке общие затраты при закупке партии в 300 ед. составят:
Ск=400∙100+350(300-101)=109,65 тыс.руб.;
а средняя цена единицы изделия в этом случае составит:
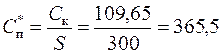 руб,/ед.
руб,/ед.
Для учета оптовых скидок наиболее часто используется дискретная зависимость Спj от Sj. При расчетах параметров модели EOQ с учетом оптовых скидок возможны различные ситуации.
Наиболее часто встречается первая ситуация, когда цена товара Спj изменяется, а затраты на хранение единицы продукции Сх, рассчитанные по формуле (5.3) в зависимости от Спj остаются постоянными.
Вторая ситуация, когда вместе с изменением цены Спj пропорционально изменяются и затраты на хранение Схj единицы продукции.
Третья ситуация при которой между изменениями цены Спj и затратами на хранение не наблюдается однозначной зависимости.
Рассмотрим последовательность расчета параметров модели EOQ для первой ситуации.
1. Зависимость суммарных затрат на приобретение, выполнение заказа и хранение записываются в виде:
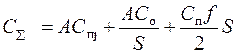 (5.17)
(5.17)
2. Выполним расчеты С∑ для различных значений S при следующих исходных данных: А=2000 ед., Со=800, f=0,2, цены для каждой единицы товара с учетом скидок приведены в табл. 5.1.
Таблица 5.1
Изменение цены единицы продукции в зависимости от размера партии заказа
| Номер j | Размер партии поставки, ед. | Цена единицы товара со скидкой, Спj руб. |
| 1-100 101-500 501 и более |
Например, при S=50 ед. находим
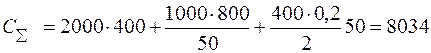 тыс. руб.
тыс. руб.
Результаты расчетов С∑ приведены в табл. 5.2.
Таблица 5.2
Результаты расчета суммарных затрат с учетом скидки
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 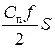 , тыс. руб. , тыс. руб.
| Суммарные затраты С∑, тыс. руб. |
| 32,0 21,3 16,0 | 2,0 3,0 4,0 | 8034,0 8024,3 8020,0 | |||
| 15,8 10,7 8,0 6,4 4,0 3,6 3,2 | 4,0 6,0 8,0 10,0 16,0 18,0 20,0 | 7019,8 7016,7 7016,0 7016,4 7020,0 7021,6 7023,2 |
Окончание табл. 5.2
| Цена единицы продукции Спj руб. | Размер заказа, S, ед. | Затраты на приобретение АСпj тыс. руб. | Затраты на выполнение заказа А∙Со/S, тыс. руб. | Затраты на хранение 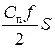 , тыс. руб. , тыс. руб.
| Суммарные затраты С∑, тыс. руб. |
| 3,2 2,9 2,7 2,5 2,3 | 20,0 22,0 24,0 26,0 28,0 | 6023,2 6024,9 6026,7 6028,5 6030,3 |
3. Рассчитаем величину оптимальной партии заказа, формула (5.6), So=200 ед. и минимальные суммарные затраты, формула (5.9) С∑min=8000 руб. Однако, из анализа результатов, приведенных в табл.5.2, следует, что минимальные затраты С∑=6023,2 тыс. руб.
Таким образом, оптимальная партия заказа с учетом скидок Sо=501 ед.; соответственно число заказов в год N=4, а периодичность поставок Т=260/4=65 дней.
Следует отметить, что формула Харриса-Уилсона выведена с учетом большого числа допущений и ограничений [26, 29]:
- затраты на выполнение заказа Co, цена поставляемой продукции Сп и затраты на хранение единицы продукции в течение рассматриваемого периода постоянны;
- период между заказами (поставками) постоянный, т. е. Тз=const;
- заказ So выполняется полностью, мгновенно;
- интенсивность спроса ( 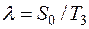 ) постоянна;
) постоянна;
- емкость склада не ограничена;
- рассматриваются только текущие (регулярные) запасы, другие виды запасов (страховые, подготовительные, сезонные, транзитные и т. д.) не учитываются.
Модифицированные варианты модели EOQ
Можно выделить следующие основные модификации классической модели EOQ: модель производственного заказа (EPQ) – подразумевает немгновенную разгрузку с одновременным расходом запаса; модель экономичного размера партии (EBQ) – подразумевает постепенное пополнение запаса (без расхода) и последующий равномерный расход; модель текущего запаса с потерей требований при дефиците; модель текущего запаса с отложенным дефицитом; комбинированные модели.
Таблица 5.3
Варианты модифицированных моделей для определения оптимального размера заказа [27]
| Наименование модели | Графическое изображение | Примечание |
| 1. Производственного заказа EPQ (Economic Production Quantity) | 
| Поступление 1; одновременное поступление и потребление 3; последующее потребление 2 |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 2. Экономичного размера партии EBQ (Economic Batch Quantity) | 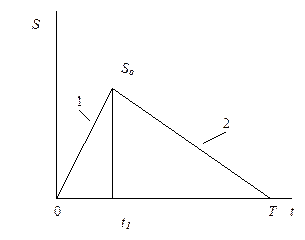
| Поступление 1 (без потребления); последующее потребление 2 |
| 3. Текущего запаса с отложенным дефицитом (I) | 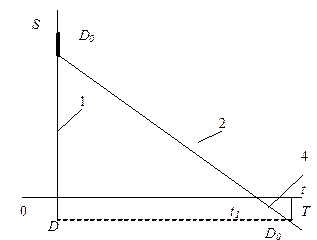
| После мгновенного поступления 1, сначала выполняется (мгновенно) отложенный спрос D0, затем этап потребления 2 и дефицита 4 |
| 4. Текущего запаса с потерей требований при дефиците (II) | 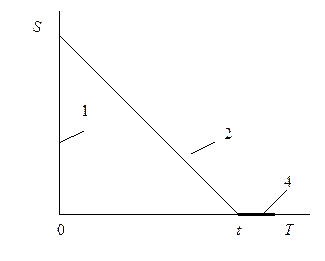
| После мгновенного поступления 1; этап потребления 2 и этап дефицита 4, когда требования не выполняются и не накапливаются |
Продолжение табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 5. Экономичного размера партии с потерей требований при дефиците | 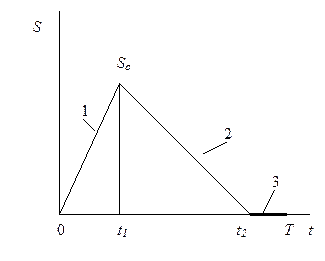
| Поступление 1 (без потребления); потребление 2; дефицит 3 (требования не выполняются и не накапливаются) |
| 6. Экономичного размера партии с дефицитом (отложенный спрос) | 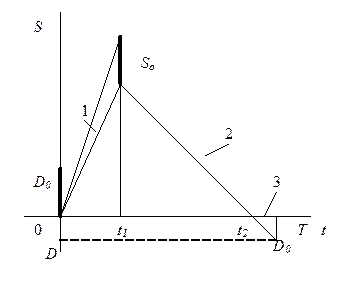
| Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); потребление 2, этап дефицита 3 (с накоплением требований). |
| 7. Производственного заказа с дефицитом (отложенный спрос) | 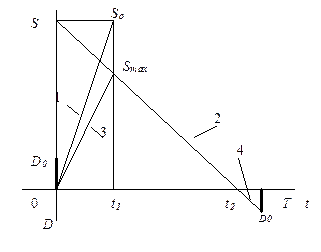
| Поступление 1 (с мгновенным выполнением отложенного спроса Dо в момент t=0); поступление с одновременным потреблением 3; потребление 2; этап дефицита 4 (с накоплением требований) |
Окончание табл. 5.3
| Наименование модели | Графическое изображение | Примечание |
| 8. Производственного заказа с потерей требований при дефиците | 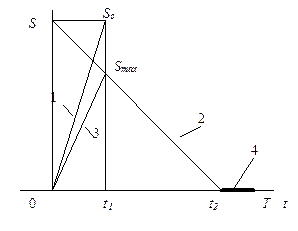
| Поступление 1; поступление с одновременным потреблением 3; потребление 2, этап дефицита (с потерей требований) |
Таблица 5.4
Откорректированные зависимости для расчета параметров модели EPQ c немгновенной разгрузкой [27, 32]
| Параметр модели | Откорректированные варианты |
| Оптимальная партия поставки, S* опт., ед. | 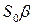 ,
где S0 – оптимальная партия рассчитанная по формуле Харриса-Уилсона ,
где S0 – оптимальная партия рассчитанная по формуле Харриса-Уилсона
|
| Количество поставок N* в плановый период D | 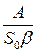
|
| Периодичность поставки Т*, дни | 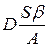
|
| Минимальные суммарные затраты С*∑, ден. ед. | 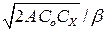
|
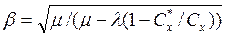 (5.18)
(5.18)
где С*Х - затраты, связанные с хранением продукции вне склада во время разгрузки транспортных средств.
μ - интенсивность пополнения;
λ - интенсивность расхода.
Пример 5.3[27]:
- потребность в заказываемом продукте А=1000 ед. в год;
- затраты на выполнение одного заказа Со=100 руб.;
- затраты на хранение единицы продукции (на складе) СХ=20 руб./ед. год;
- количество рабочих дней в году D=250 дней;
- интенсивность пополнения запасов на склад μ =25 ед./день;
- интенсивность расхода запаса со склада λ=4 ед./день;
- затраты на хранение доставленной продукции вне склада С*Х =40 руб./ед. год
Рассчитаем S0, для этого воспользуемся формулой (5.6):
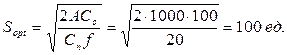
По формуле (5.18) найдем значение поправочного коэффициента β:
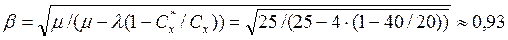
Теперь можно определить параметры модели EPQ и рассчитать суммарные минимальные затраты:
- оптимальная партия поставки:
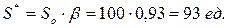
- оптимальное количество поставок:
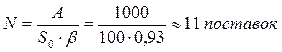
- оптимальная периодичность поставок:
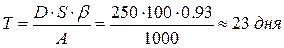
- суммарные минимальные затраты:
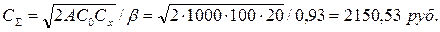
Таблица 5.5
Откорректированные зависимости для расчета показателей модели экономичного размера партии (EBQ) [27, 32]
| Наименование показателя | Откорректированные зависимости |
| 1. Экономичный (оптимальный) размер партии S*, ед. | 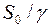
|
| 2. Количество партий поставок N*в плановом периоде D | 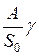
|
| 3. Продолжительность одного цикла поставки Т*, дни | 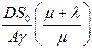
|
4. Минимальные суммарные затраты 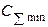 , руб. , руб.
| 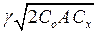
|
Корректирующий коэффициент 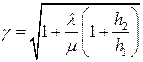 , (5.19)
, (5.19)
где h2 – затраты на хранение в транспортном средстве;
h1 – затраты на хранение на складе;
μ - интенсивность пополнения;
λ - интенсивность расхода.
Пример 5.4:
Пусть нам известно следующее:
- потребность в заказываемом продукте (А)=1000 ед. в год;
- затраты на выполнение одного заказа (Со)=100 руб.;
- затраты на хранение единицы продукции на складе (h1 или Сх) =20 руб./ед. год;
- затраты на хранение доставленной продукции в транспортном средстве (h2) = 40 руб./ед. год
- количество рабочих дней в году (D)=250 дней;
- интенсивность пополнения запасов на склад (μ)=25 ед./день;
- интенсивность расхода запаса со склада (λ) = 4 ед./день;
Рассчитаем S0:
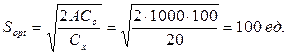
По формуле (5.19) найдем значение поправочного коэффициента γ:
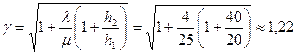
Теперь рассчитаем параметры модели EBQ и определим суммарные минимальные затраты:
- оптимальная партия поставки:
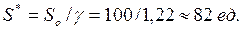
- оптимальное количество поставок:
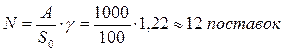
- оптимальная периодичность поставок:
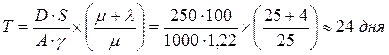
- суммарные минимальные затраты:
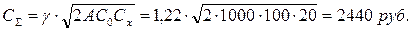
Дата добавления: 2016-01-07; просмотров: 2383;
