Момент инерции относительно произвольной оси. Тензор инерции.
Введенные формулами (3.26), (3.27) величины оказываются существенно необходимыми при изучении динамики вращательных движений твердого тела или системы тел. Эти характеристики инерции зависят как от положения начала координат, так и от направлений выбранных координатных осей. Однако в данной точке тела шесть величин  вместе с суммарной массой М полностью определяют его инерцию. Иначе говоря, зная эти величины, можно найти момент инерции относительно оси произвольного направления и центробежный момент инерции для пары новых (повернутых) осей, а также, при известной геометрии тела, перейти к инерционным характеристикам, определенным для другого начала координат. Пусть требуется найти момент инерции относительного заданного направления (оси ξ), характеризуемого ортом
вместе с суммарной массой М полностью определяют его инерцию. Иначе говоря, зная эти величины, можно найти момент инерции относительно оси произвольного направления и центробежный момент инерции для пары новых (повернутых) осей, а также, при известной геометрии тела, перейти к инерционным характеристикам, определенным для другого начала координат. Пусть требуется найти момент инерции относительного заданного направления (оси ξ), характеризуемого ортом 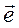 . Моментом инерции системы материальных точек относительно оси называется сумма произведений масс этих точек на квадраты их расстояний до оси
. Моментом инерции системы материальных точек относительно оси называется сумма произведений масс этих точек на квадраты их расстояний до оси

Легко сообразить, что квадрат расстояния h, , можно подсчитать по формуле (рис. 53)
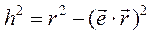 (3.28)
(3.28)
где 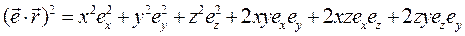 3.28а)
3.28а)
Запишем полученное выражение (3.29) иначе
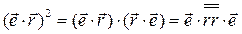 (3.29)
(3.29)
 Мы изменили порядок сомножителей во втором скалярном произведении и отбросили скобки; первое делать можно, а второе? При этом появилась новая величина
Мы изменили порядок сомножителей во втором скалярном произведении и отбросили скобки; первое делать можно, а второе? При этом появилась новая величина 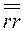 , в которой два вектора перемножаются, но не скалярно и не векторно, а каким-то новым способом; такое умножение называетсядиадным (или тензорным),а само произведение - диадой, которая представляет собой тензор второго ранга. Аналитическое определение тензора состоит в следующем: совокупность Зn величин (в трехмерном пространстве), преобразующихся при повороте координатной системы как произведения n координат, называется тензором n-го ранга. По этому определению диада будет тензором 2-го ранга, вектор -тензором 1-го ранга, а скалярная величина — тензором нулевого ранга. Очевидно, что диада
, в которой два вектора перемножаются, но не скалярно и не векторно, а каким-то новым способом; такое умножение называетсядиадным (или тензорным),а само произведение - диадой, которая представляет собой тензор второго ранга. Аналитическое определение тензора состоит в следующем: совокупность Зn величин (в трехмерном пространстве), преобразующихся при повороте координатной системы как произведения n координат, называется тензором n-го ранга. По этому определению диада будет тензором 2-го ранга, вектор -тензором 1-го ранга, а скалярная величина — тензором нулевого ранга. Очевидно, что диада 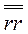 не изменится при перестановке ее сомножителей - это симметричная диада. Более общий случай получим, перемножая два разных вектора, например
не изменится при перестановке ее сомножителей - это симметричная диада. Более общий случай получим, перемножая два разных вектора, например  и
и  ; диада
; диада 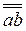 уже не будет симметричнойи переставлять сомножители у нее нельзя:
уже не будет симметричнойи переставлять сомножители у нее нельзя:
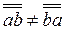 .
.
Так как векторы 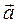 и
и  можно представить в виде
можно представить в виде

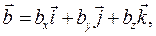
то диада 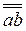 может быть записана в виде суммы девяти слагаемых
может быть записана в виде суммы девяти слагаемых
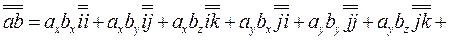
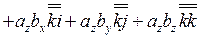 (3.30)
(3.30)
Здесь 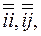 …..
….. 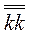 элементарные диады, а коэффициенты при них называются составляющими или компонентами тензора. Тензор второго ранга (диаду) можно записать также в виде квадратной матрицы. Так, для тензора (3.30)
элементарные диады, а коэффициенты при них называются составляющими или компонентами тензора. Тензор второго ранга (диаду) можно записать также в виде квадратной матрицы. Так, для тензора (3.30)
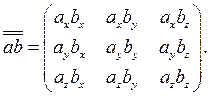 (3.31)
(3.31)
Хотя развернутый вид (3.30) тензора 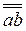 и не имеет табличного вида (3.31), однако положение каждой составляющей в таблице устанавливается сразу по ее множителю - элементарной диаде: левый орт указывает строку, а правый орт - столбец, орты соответствуют положению данной составляющей в матрице (3.31). Теперь легко понять неравенство
и не имеет табличного вида (3.31), однако положение каждой составляющей в таблице устанавливается сразу по ее множителю - элементарной диаде: левый орт указывает строку, а правый орт - столбец, орты соответствуют положению данной составляющей в матрице (3.31). Теперь легко понять неравенство 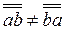 ; перестановка сомножителей в диаде
; перестановка сомножителей в диаде 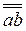 означает замену строк столбцами (и наоборот) в матрице (3.31), а тензор
означает замену строк столбцами (и наоборот) в матрице (3.31), а тензор  будет транспонированным по отношению к первоначальному тензору
будет транспонированным по отношению к первоначальному тензору 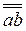 .Из теории матриц известно, что квадратную матрицу (3.31) можно умножить справа на вектор-столбец или слева на вектор-строку. Запись тензора в форме (3.30) позволяет эти операции свести к скалярному умножению ортов. Тензор второго ранга
.Из теории матриц известно, что квадратную матрицу (3.31) можно умножить справа на вектор-столбец или слева на вектор-строку. Запись тензора в форме (3.30) позволяет эти операции свести к скалярному умножению ортов. Тензор второго ранга 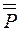 можно умножить скалярно как справа, так и слева на вектор а; при этом результат будет различным, так как при правом умножении тензора на вектор будут появляться скалярные произведения правых ортов элементарных диад на орты вектора, а при левом умножении вектора на тензор в скалярных произведениях будут участвовать левые орты элементарных диад. В результате останутся орты элементарных диад, которые не участвовали в скалярных произведениях, поэтому скалярное произведение тензора и вектора будет векторной величиной. Легко сообразить, что
можно умножить скалярно как справа, так и слева на вектор а; при этом результат будет различным, так как при правом умножении тензора на вектор будут появляться скалярные произведения правых ортов элементарных диад на орты вектора, а при левом умножении вектора на тензор в скалярных произведениях будут участвовать левые орты элементарных диад. В результате останутся орты элементарных диад, которые не участвовали в скалярных произведениях, поэтому скалярное произведение тензора и вектора будет векторной величиной. Легко сообразить, что 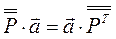 , где
, где 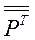 означает транспонированный тензор. В случае симметричного тензора транспонированный тензор равен первоначальному и разница между правым и левым произведениями исчезает. В нашем случае
означает транспонированный тензор. В случае симметричного тензора транспонированный тензор равен первоначальному и разница между правым и левым произведениями исчезает. В нашем случае 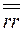 симметричный тензор и его развернутое выражение типа (3.29) оказывается проще:
симметричный тензор и его развернутое выражение типа (3.29) оказывается проще:
 (3.32)
(3.32)
Если тензор (второго ранга) умножать скалярно на векторы и слева, и справа, то участвовать в скалярных произведениях будут как левые, так и правые орты элементарных диад, и в результате получится скалярная величина. Именно это мы имеем в формуле (3.29). Записывая эту формулу в виде
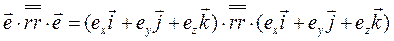 , (3.33)
, (3.33)
где тензор 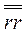 представлен выше в виде (3.32), сразу понимаем, что в результате двойного скалярного перемножения в (3.33) исчезают те слагаемые, в которых встречаются произведения (скалярные) разных ортов. Остающиеся слагаемые легко написать сразу; это будут те же компоненты тензора
представлен выше в виде (3.32), сразу понимаем, что в результате двойного скалярного перемножения в (3.33) исчезают те слагаемые, в которых встречаются произведения (скалярные) разных ортов. Остающиеся слагаемые легко написать сразу; это будут те же компоненты тензора 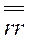 ,что и представленные в формуле (3.32), только орты в этой формуле следует заменить на соответствующие проекции вектора
,что и представленные в формуле (3.32), только орты в этой формуле следует заменить на соответствующие проекции вектора 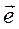 . Тогда получим
. Тогда получим
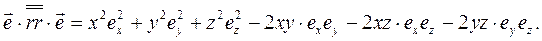 (3.34)
(3.34)
Сравнивая результат (3.34) с формулой (3.38а), убеждаемся и законности опускания скобок в формуле (3.29). Простейшим тензором второго ранга будет единичный тензор:
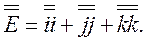 (3.35)
(3.35)
Нетрудно сообразить, что диагональные элементы матрицы, соответствующей тензору (3.35), будут единицами, а остальные, недиагональные — нулями. Название «единичный тензор» совершенно оправдано, так как, умножая на него любой вектор  (справа или слева - это безразлично), мы опять получим вектор
(справа или слева - это безразлично), мы опять получим вектор  :
:
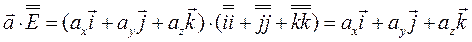 =
= 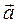
Это свойство единичного тензора 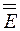 приводит к следующему интересному соотношению:
приводит к следующему интересному соотношению:
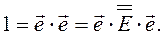 (3.36)
(3.36)
Соотношения (3.36) и (3.29) позволяют написать формулу (3.28) В ином виде
 (3.37)
(3.37)
Далее, подставляя эту формулу в интеграл для 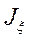 , получаем следующее выражение для момента инерции
, получаем следующее выражение для момента инерции
 =
=  (3.38)
(3.38)
Величина
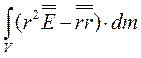 =
= 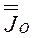 , (3.39)
, (3.39)
вошедшая в выражение для 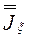 (формула 3.38), представляет собой тензор инерции твердого тела в точке О.Вводя этот тензор, переписываем формулу (3.38) для момента инерции относительно оси
(формула 3.38), представляет собой тензор инерции твердого тела в точке О.Вводя этот тензор, переписываем формулу (3.38) для момента инерции относительно оси  , заданной направлением орта
, заданной направлением орта 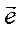 , в очень простом виде
, в очень простом виде
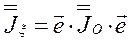 (3.40)
(3.40)
Если подставить развернутые диадные представлении тензора  и
и 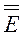 в определение тензора
в определение тензора 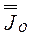 и учесть формулы (3.26) и (3.27), получаем диадное представление для тензора инерции
и учесть формулы (3.26) и (3.27), получаем диадное представление для тензора инерции
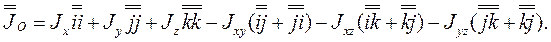 (3.41)
(3.41)
Подставим выражение (52) в формулу (51), тогда получим
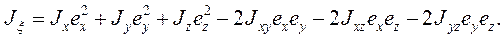 (3.42)
(3.42)
Формула (3.40) представляет краткую тензорную запись развернутого представления (3.42). Найдем теперь центробежный момент инерции для пары новых осей  , орты которых
, орты которых  и
и  перпендикулярны друг другу, т. е.
перпендикулярны друг другу, т. е. 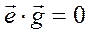 . По определению центробежный момент инерции
. По определению центробежный момент инерции 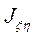 равен
равен 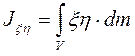
Но  , а
, а  , поэтому
, поэтому
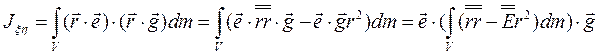 Здесь использовано условие ортогональности
Здесь использовано условие ортогональности  и
и 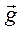 и определение единичного тензора
и определение единичного тензора  . Вспоминая формулу (3.39) для тензора инерции, получаем окончательно
. Вспоминая формулу (3.39) для тензора инерции, получаем окончательно
 . (3.43)
. (3.43)
Развёрнутый вид формулы (3.43) получим, произведя фактическое перемножение ортов 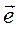 ,
,  и тензора (3.41):
и тензора (3.41): 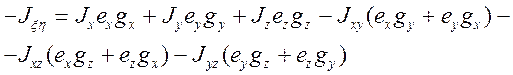 (3.44)
(3.44)
Дата добавления: 2016-01-07; просмотров: 1972;
