Вычисление моментов инерции.

Вычисление моментов инерции тел производится методами интегрального исчисления (по формулам 33а, 34а). Однако можно в некоторых случаях сосчитать моменты инерции простых тел, без вычислений тройных интегралов.

1. Момент инерции тонкого однородного стержня (рис. 54).

Направим ось ОХ по стержню, а ось ОY перпендикулярно, через центр стержня.

,

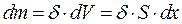здесь δ -плотность стержня, S - площадь поперечного сечения. Тогда, вместо тройного интеграла можно написать

,

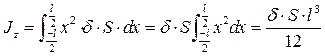но 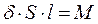, откуда 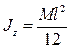. Ось ОZ –главная ось инерции ( ось симметрии), следовательно, .

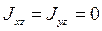2. Момент инерции однородного круглого цилиндра относительно его оси. За элемент объема примем цилин­дрический слой, образуемый двумя коа­ксиальными цилиндрами радиусов h и h+dh. Получим: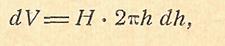

С другой стороны, 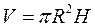, где R — радиус цилиндра, следовательно

и окончательно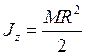

Момент инерции полого цилиндра с внешним радиусом R и внутренним Ro найдем как разность моментов инерции сплошных цилиндров этих же радиусов:

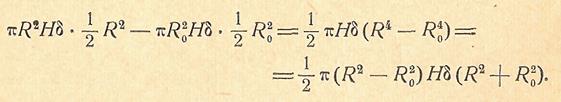
Итак, момент инерции полого цилиндра равен

,

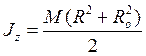где М - масса полого цилиндра. Моменты инерции некоторых однородных тел приведены в таблице. Момент инерции имеет размерность массы, умноженной на квадрат длины. Отношение 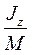имеет размерность квадрата длины и обозначается через 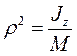. Величина ρ-называется радиусом инерции и

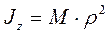. (3.48)

Таблица моментов инерции однородных тел представлена ниже.