Переходные процессы двигателей с линейной характеристикой

При работе электропривода существуют следующие переходные процессы:

· механические – связанные с изменением кинетической и потенциальной энергии системы. Они характеризуются механической постоянной времени (Т_М = 0,1…10 с);

· электромагнитные – возникают при изменении электромагнитной энергии системы (Т_Я= 0,01…0,1с);

· электромеханические переходные процессы (Т_М , Т_Я);

· тепловые – обусловленные изменением запаса тепловой энергии. Вызывают изменение активного сопротивления обмоток, т.е. влияют на электромеханические переходные процессы, но протекают значительно медленнее последних. (Т_н= 10³ с).

Из общего дифференциального уравнения двигателя постоянного тока при i_c = const, , , ,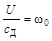

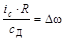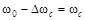Получаем

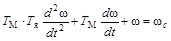МЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

При анализе механических переходных процессов учитывают только механическую инерционность системы. Поскольку T_М>> T_Я, то пренебрегая T_Я=0, получаем

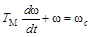Физическое толкование T_М: время разгона электропривода до скорости идеального холостого хода при постоянном пусковом моменте М_П = М_КЗ и отсутствии нагрузки на валу М_С = 0. Решение уравнения имеет вид

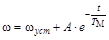где ω_уст = ω_с; (Т_Мр + 1 = 0).

Постоянная интегрирования А определяется из начальных условий переходного процесса. В общем случае при t = 0 ,ω = ω_нач

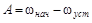Тогда

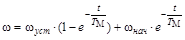В частном случае, когда ω_нач= 0(при пуске)

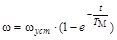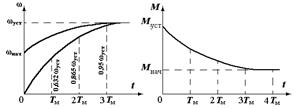
Если в уравнение подставить время t в долях от T_М, то можно составить таблицу

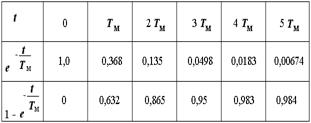
Из этих данных видно, что при t = 3T_М скорость вращения двигателя отличается от установившегося значения на 5%, а при t = 4T_М на 2%. Поэтому переходной процесс считают закончившимся при t = (3÷4)T_М.

Аналогично закон изменения момента и тока во времени

; .

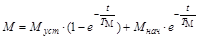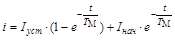Для определения T_М нужно знать приведенный момент инерции J. Его можно найти экспериментально с помощью режима свободного выбега. До отключения двигатель работал в установившемся режиме с моментом

.

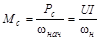После отключения двигателя поведение электропривода, если принять M_C = const, описывается

.

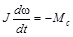Замеряют время торможения и определяют

.

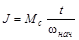ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

Электромагнитные переходные процессы обусловлены изменением запаса электромагнитной энергии в электрических машинах, пропорциональной индуктивности их цепей и квадрату протекающего по ним тока. Длительность определяется индуктивностью обмоток.

Если к зажимам обмотки, обладающей индуктивностью L_В и омическим сопротивлением R_В, приложить постоянное напряжение U_В, то уравнение ЭДС для цепи, обмотки возбуждения ДПТ выразится следующим образом

.

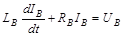Разделив правую и левую части на R_В, получим дифференциальное уравнение первого порядка

,

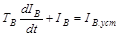где: ; .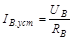

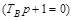Физический смысл электромагнитной постоянной времени: это время, в течение которого ток в контуре, содержащем индуктивность, изменяется от нуля до установившегося значения, определяющегося величиной приложенного напряжения и омического сопротивления контура.

Решение уравнения для общего случая, когда при t= 0начальное значение тока i = I_нач

.

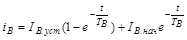Продолжительность переходного процесса приблизительно (3÷4)T_В_.

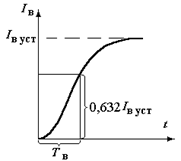
Ориентировочно:

Р = (1÷100)кВт→T_В = (0,1÷1)с;

Р = (100 ÷1000)кВт→T_В = (1÷2)с;

Р = (1000÷3000)кВт→T_В =(2÷4)с.

Продолжительность нарастания тока может быть значительной (3÷4)T_В, что приводит к уменьшению быстродействия. Для сокращения времени переходного процесса применяют форсировку возбуждения – различные способы ускорения нарастания тока возбуждения.

ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

Решение общего дифференциального уравнения

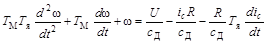
зависит от корней его характеристического уравнения

,

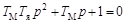которые равны

.

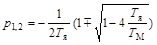В зависимости от соотношения постоянных времени корни характеристического уравнения, а следовательно, и характер протекания переходного процесса будут различными.

1. При Т_М> 4Т_Якорни будут вещественными и отрицательными

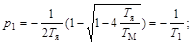çр₁ ç < ç р₂ ç;

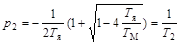; T₁ > T₂,

где: Т₁ и Т₂- фиктивные постоянные времени, с.

Полное решение уравнения имеет вид:

,

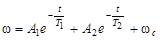где: A₁ и А₂ - постоянные интегрирования.

Дифференцируя по времени последнее выражение, найдем закон изменения ускорения .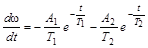

Ток якоря получим из уравнения движения

.

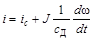Подставляя в это выражение значение найденного ускорения, находим закон изменения тока якоря

,

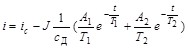В общем случае начальные условия процесса равны (при t=0): 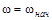и .

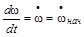Подставляя эти значения в соответствующие выражения, получим

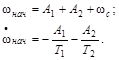
Определим коэффициенты A₁ и A₂

;

.

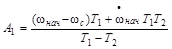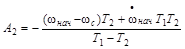Начальные значения скорости и тока и их установившиеся величины определяются по статическим характеристикам. При пуске вхолостую начальные значения тока и скорости могут быть приняты равными нулю ; при пуске под нагрузкой ω_нач = 0 и I_нач = I_с.

Графики изменения скорости и тока во времени при пуске вхолостую.

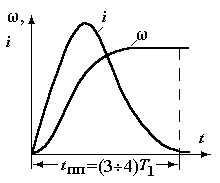
Длительность переходного процесса определяется большей из двух постоянных времени.

2. При Т_М= 4Т_Якорни характеристического уравнения будут кратными, равными

.

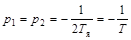Решение дифференциального уравнения

.

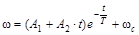Коэффициенты A₁ и A₂находят аналогично первому случаю.

Переходные процессы являются апериодическими с длительностью t_пп = (3÷4)Т, меньше, чем в первом случае (Т<T₁).

3. При Т_М< 4Т_Якорни становятся комплексными

; ,

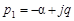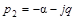где ;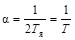

.

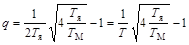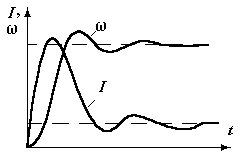
Переходной процесс будет колебательным с частотой q.

Решение уравнения

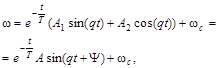
где ; .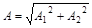

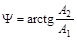Переходной процесс затухающий и оканчивается за время t_пп ≈ (3÷4)Т.

<12 13 141516 17 18 >

Дата добавления: 2016-01-07; просмотров: 1670;