Переходные процессы при торможении

ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ПРОТИВОВКЛЮЧЕННИ

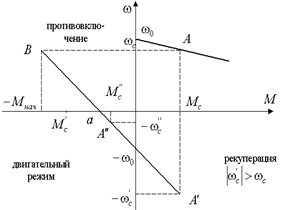
При переключении в режим противовключения переходим из точки 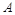в точку В. В точке 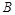момент отрицательный и направлен в сторону, противоположную движению, т.е. тормозной. Происходит торможение по левой характеристике. В точке ”а” двигатель нужно отключить и наложить тормоз. Если статический момент имеет потенциальный характер, то двигатель разгонится до т. 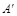, т.е. будет работать в режиме рекуперации со скоростью .

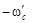Если момент статический реактивный, то возможны два случая

· ;

· .

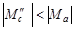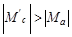В первом случае двигатель разгонится в противоположном направлении до точки А^’’ со скоростью 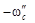(двигательный режим). Во втором случае двигатель не будет вращаться.

Начальная скорость определяется скоростью в т. А

.

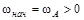Начальный момент определяется моментом в т. В

.

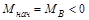Установившееся значение скорости определяется скоростью в т.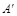

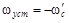(штрих опустим); .

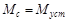Зависимость w(t) и М(t) имеют следующий вид

;

;

.

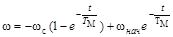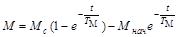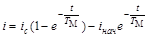Кривые переходных процессов

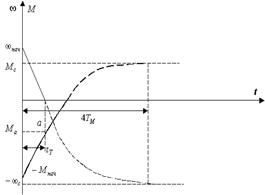
Определим время торможения в режиме противовключения 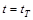. Используя уравнение w(t) при 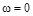, получим

,

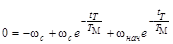откуда

.

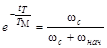Логарифмируя это выражение, находим

.

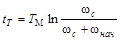ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ЭЛЕКТРОДИНАМИЧЕСКОМ ТОРМОЖЕНИИ

Сделав переключение из точки 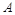, попадаем в точку 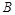, а потом по характеристике в точку 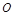. Если двигатель не затормозить, то он начнет разгоняться и перейдет в точку 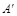(при потенциальном статическом моменте).

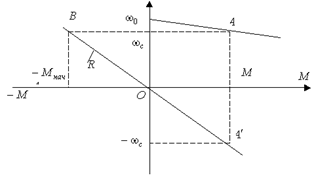
Если момент статический реактивный, то когда двигатель окажется в точке 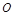, система будет стоять. Начальные и конечные условия

; .

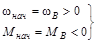
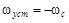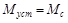Тогда

;

.

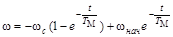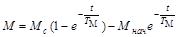Построим кривые переходных процессов для режима динамического торможения. Уравнения одинаковы, как и для режима противовключения, но переменные различны по абсолютной величине.

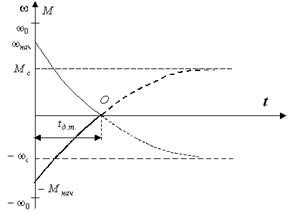
Пунктирной линией показаны кривые при потенциальном моменте. Пусть за время 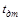скорость изменилась от начальной до нуля. Тогда запишем

.

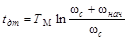Полученные выражения справедливы при 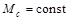. Если 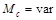, то необходимо рассчитывать переходные процессы графическим или графо-аналитическим методами.