Линейные преобразования сигналов и ФУ

Линейные ФУ по определению описываются линейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей) с постоянными коэффициентами. С точки зрения схемотехники это значит, что все элементы ФУ (R, C, L) имеют постоянные параметры. Оператором преобразования воздействия x(t) в реакцию y(t) для них может служить одна из форм интеграла наложения (Дюамеля) во временной области

,

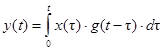или передаточная функция Н 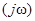ФУ в частотной области

,

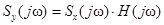а в качестве функциональной характеристики линейного ФУ можно использовать его импульсную характеристику или передаточную функцию Н .

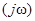Простым колебанием для линейных цепей является гармоническое 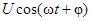. Его форма не изменяется при прохождении через любую линейную цепь. В линейных цепях действует принцип суперпозиции – реакция цепи на сумму воздействий есть сумма её реакций на каждое из воздействий в отдельности. Из этих свойств вытекают следующие выводы:

1. Форма сложного сигнала (с полигармоническим или сплошным спектром) при его прохождении через линейную цепь может изменяться только вследствие изменения соотношения между амплитудами и фазами спектральных составляющих воздействия. Принципиально важно, что в реакции линейного ФУ не могут возникнуть спектральные компоненты, отсутствующие в спектре воздействия.

2. Из вывода 1 вытекают возможности построения на основе линейных цепей ограниченного класса типовых ФУ:

а) усилителей и аттенюаторов (ФУ для изменения мощности сигналов без искажения их формы), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид

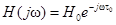, где Н₀ и t₀ – константы;

б) фильтров разных типов (ФНЧ, ФВЧ, ПФ, РФ, интеграторов, дифференциаторов, фазовращателей и т.п.), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид

,

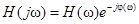где Н(w) (АЧХ) и j(w) (ФЧХ) – заданные функции частоты.