Зависимость между моментами силы относительно
Точки и оси, проходящей через эту точку
| Рис. 28 |
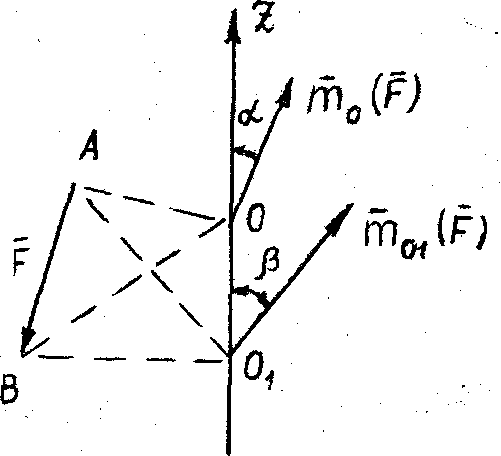Теорема. Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки, взятой на оси.
Согласно этой теореме (рис. 28),
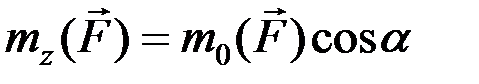
и
.
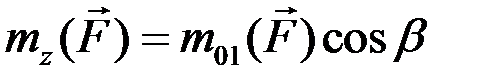Аналитические выражения моментов силы
Относительно координатных осей
На тело в точке А (x,y,z) (рис. 29) действует сила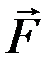 
. Проекции силы на оси координат равны 
.
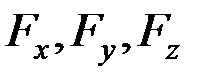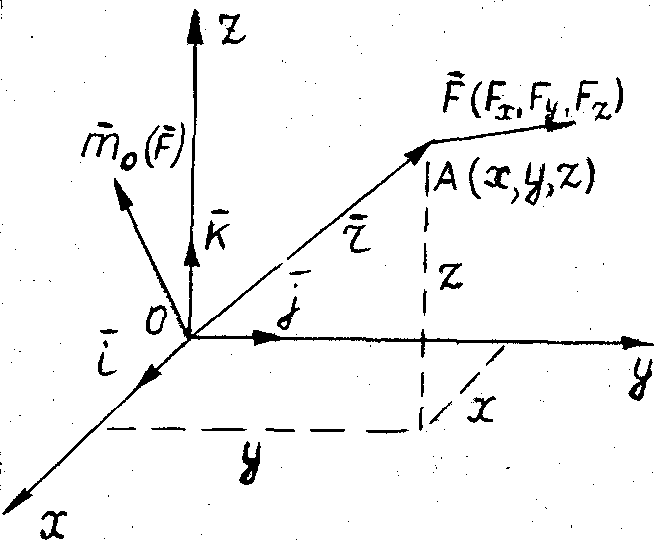
Представим векторное равенство (2.3) в виде определителя Рис. 29
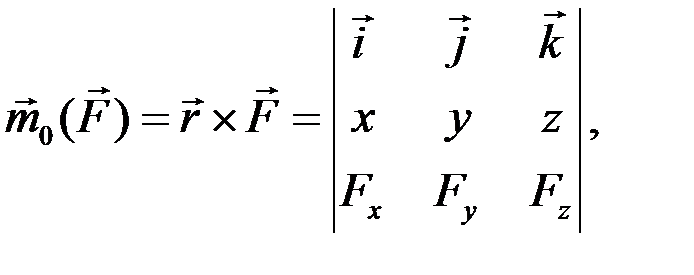(2.4)
где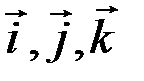 
– орты осей Ox, Oу, Оz.
Разложим определитель (2.4) по элементам верхней строки
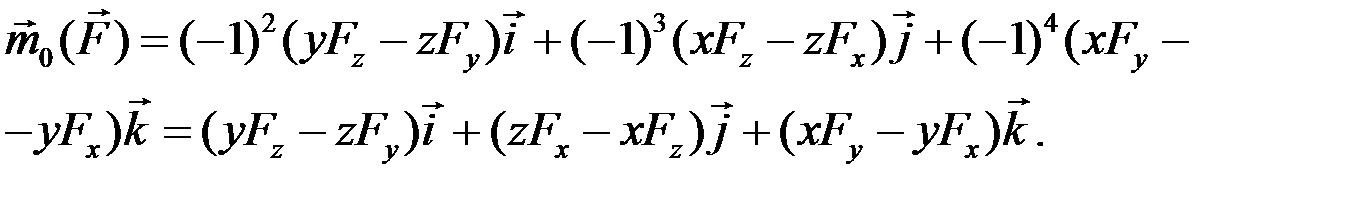(2.5)
Разложим вектор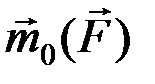 
на составляющие по осям координат
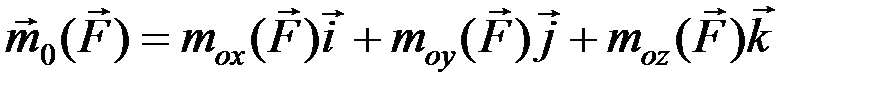. (2.6)
В равенствах (2.5) и (2.6) равны левые части, значит, равны и правые части. Следовательно, равны в этих равенствах сомножители перед ортами 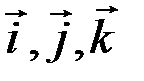. Отсюда получаем аналитические выражения моментов силы относительно координатных осей:
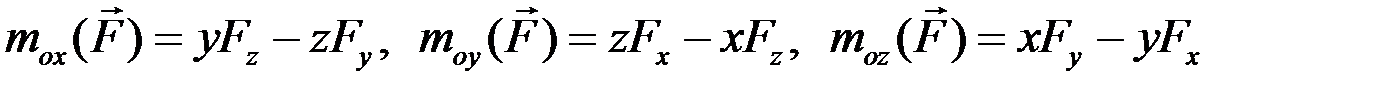. (2.7)
Пример
Используя выражения (2.7), найти моменты силы в примере, рассмотренном в параграфе 2.3. (см. рис. 27), относительно координатных осей.
Решение
Из условия задачи находим координаты точки K приложения силы и проекции силы на оси координат:
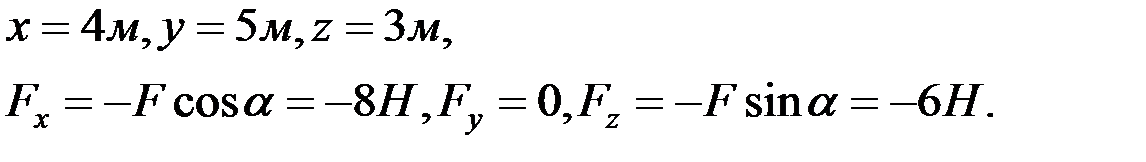
Используя выражения (2.7), определяем моменты силы относительно координатных осей:
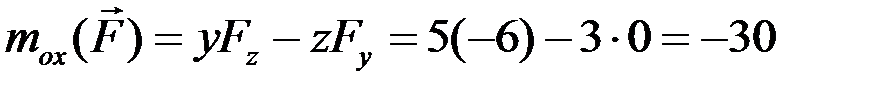(Н×м);
;
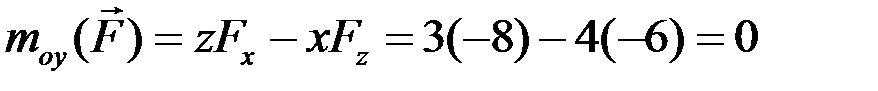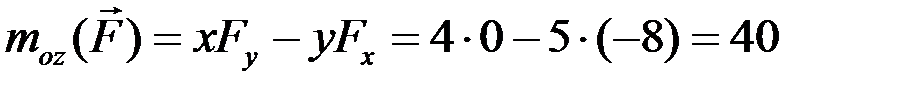(Н×м).
Дата добавления: 2016-01-03; просмотров: 1147;