Сложение пар в пространстве и на плоскости
Теорема. Действующую на абсолютно твёрдое тело пространственную систему пар можно заменить одной парой, момент которой равен геометрической сумме моментов действующих пар.
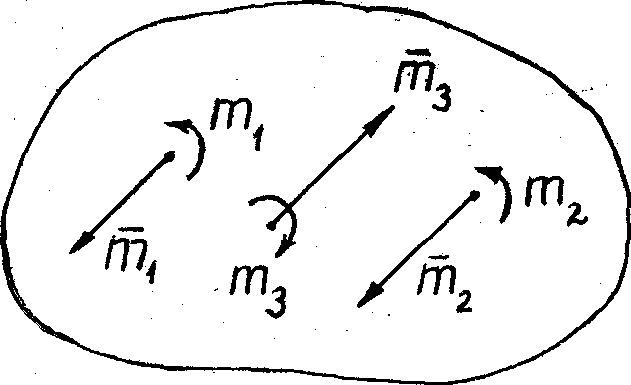
Пары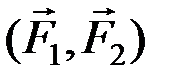 
и 
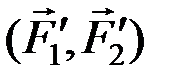, лежащие в пересекающихся плоскостях I и II и имеющие моменты 
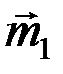и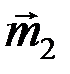 
(рис. 36), согласно этой теореме можно заменить одной парой 
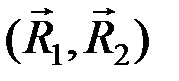, момент которой равен
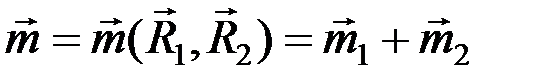. (2.8)
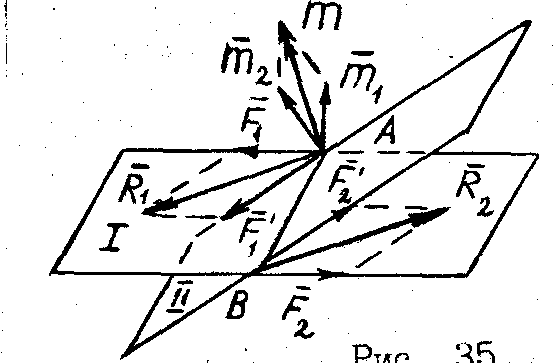
| Рис. 36 |
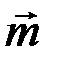определяется диагональю параллелограмма, построенного на векторах 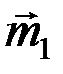и .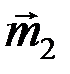
Частный случай сложения пар на плоскости.
Если на тело действует плоская система пар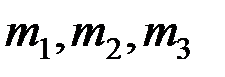 
, то их векторы 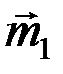, 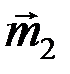и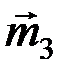 
параллельны (рис. 37). Модуль результирующего вектора системы параллельных векторов равен алгебраической сумме их модулей:
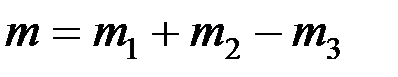. (2.9)
| Рис. 37 |
Отсюда следует, что плоскую систему пар можно заменить одной парой, момент которой равен алгебраической сумме моментов пар системы.
Условия равновесия пространственной и плоской
Систем пар
Для равновесия пространственной системы пар необходимо и достаточно, чтобы момент результирующей пары (2.8) равнялся нулю
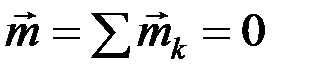. (2.10)
| Рис. 38 |
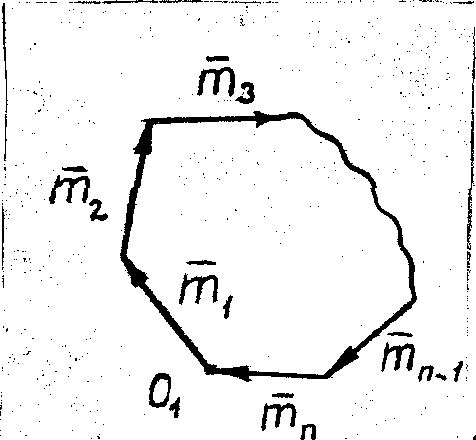Геометрические условия равновесия (2.10) выражаются в замкнутости многоугольника пар самого на себя (рис. 38): конец последнего вектора 
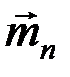приходит в начало первого.
Аналитические условия равновесия пространственной системы пар получим, спроектировав векторное равенство (2.10) на три координатные оси:
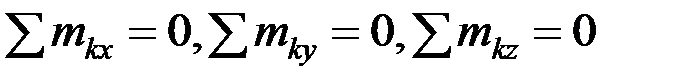. (2.11)
Для равновесия пространственной системы пар необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю. С учётом того, что пары на плоскости суммируются алгебраически, аналитическое условие равновесия плоской системы пар получим, приравняв равенство (2.9) к нулю:
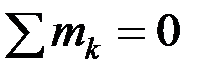. (2.12)
Для равновесия плоской системы пар необходимо и достаточно, чтобы их алгебраическая сумма равнялась нулю.
Дата добавления: 2016-01-03; просмотров: 1180;