Умножение матрицы на число.
Произведением матрицы 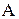 на число
на число 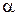 называется матрица
называется матрица 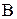 той же размерности, у которой каждый элемент
той же размерности, у которой каждый элемент 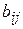 равен произведению элементов
равен произведению элементов 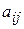 на число
на число 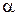 :
: 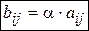 .
.
Пример 3. Дана матрица 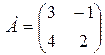 . Найти
. Найти 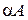 , если
, если 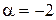 .
.
Решение. 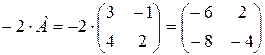 .
.
Матрица 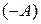 называется противоположной для матрицы
называется противоположной для матрицы 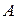 .
.
Вычитание матриц.
Разностью матрицодинаковой размерности А и В называется матрица D той же размерности, элементы которой равны разности соответствующих элементов матриц А и В: 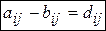
6. Умножение матриц.
Произведением матрицы 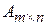 на матрицу
на матрицу 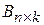 называется матрица
называется матрица 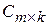 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) матрица 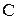 существует, если число столбцов
существует, если число столбцов 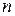 первого сомножителя
первого сомножителя 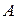 равно числу строк
равно числу строк 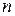 второго сомножителя
второго сомножителя 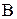 ;
;
2) элемент 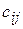 матрицы
матрицы 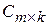 равен сумме произведений элементов
равен сумме произведений элементов 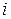 -ой строки матрицы
-ой строки матрицы 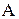 на элементы
на элементы 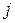 -ого столбца матрицы
-ого столбца матрицы 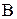 :
:
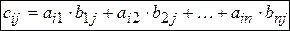 ;
;
3) число строк 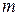 матрицы
матрицы 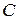 равно числу строк
равно числу строк 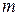 матрицы
матрицы 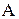 , а число столбцов
, а число столбцов 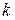 матрицы
матрицы 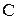 равно числу столбцов
равно числу столбцов 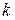 матрицы
матрицы 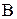 .
.
Порядок умножения матриц А и В очень важен. Число столбцов ( 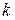 ) первого множителя должно равняться числу строк второго множителя. Вообще говоря,
) первого множителя должно равняться числу строк второго множителя. Вообще говоря, 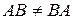 .
.
Пример 4. Даны матрицы 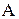 и
и 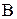 . Найти произведение
. Найти произведение 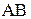 .
.
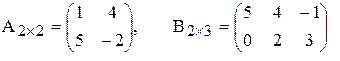
Решение. 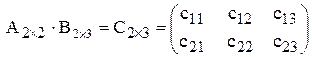


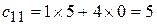
№ строки  № столбца
№ столбца 
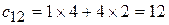 , и так далее.
, и так далее.
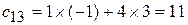 ,
,
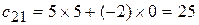 ,
,
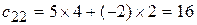 ,
,
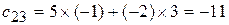 .
.
Итак, матрица 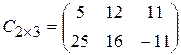 .
.
Дата добавления: 2015-12-22; просмотров: 560;
