Действия с матрицами
Матрицы и определители
Матрицы и их виды
Матрицей размерности 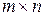 называется таблица чисел, расположенных в
называется таблица чисел, расположенных в 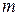 строках и
строках и 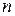 столбцах:
столбцах:
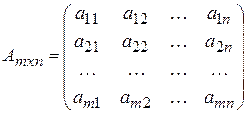 ,
,
Матрицы обозначаются латинскими буквами А, В, С, …
Числа, составляющие матрицу, называются ее элементами.
Каждый элемент 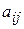 имеет два индекса
имеет два индекса 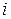 - номер строки,
- номер строки, 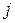 -номер столбца, на пересечении которых стоит элемент
-номер столбца, на пересечении которых стоит элемент 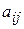 .
.
Для матриц используют обозначение 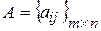 или
или 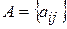 ,
, 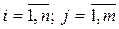 .
.
Пример 1. Матрицы 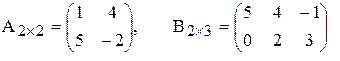
Матрица, у которой число строк равно числу столбцов ( 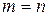 ), называется квадратной, иначе матрица называется прямоугольной. Элементы квадратной матрицы
), называется квадратной, иначе матрица называется прямоугольной. Элементы квадратной матрицы 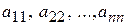 , для которых
, для которых 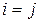 , называются диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю.
, называются диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю.
Примеры матриц различных видов:
Верхняя треугольная – квадратная матрица, у которой элементы, стоящие ниже главной диагонали, равны 0:
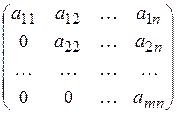
| Нижняя треугольная – квадратная матрица, у которой элементы, стоящие выше главной диагонали, равны 0:
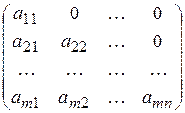
|
Диагональная – квадратная матрица, у которой все элементы, кроме диагональных, равны 0:
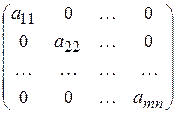
| Единичная – квадратная матрица, у которой элементы, стоящие на главной диагонали, равны 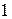 , а остальные элементы равны , а остальные элементы равны 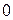 : :
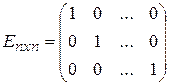
|
Матрица-столбец: 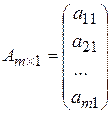 . .
| Матрица-строка: 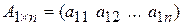 . .
|
Действия с матрицами
1. Равенство матриц.
Матрица 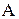 называется равной матрице
называется равной матрице 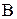 , если они одинаковой размерности и их соответствующие элементы равны.
, если они одинаковой размерности и их соответствующие элементы равны.
2. Транспонирование матриц.
Если в матрице 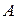 строки записать в виде столбцов с теми же номерами, то получим матрицу, транспонированную матрицу
строки записать в виде столбцов с теми же номерами, то получим матрицу, транспонированную матрицу 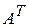 . Она обозначается
. Она обозначается 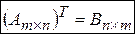 .
.
Пример 2. Дана матрица 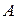 . Получить матрицу
. Получить матрицу 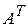 .
.
Решение. 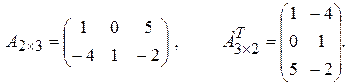
3. Сложение матриц.
Суммой матриц 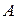 и
и 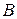 одинаковой размерности называется матрица
одинаковой размерности называется матрица 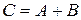 такой же размерности, каждый элемент которой равен сумме соответствующих элементов матриц
такой же размерности, каждый элемент которой равен сумме соответствующих элементов матриц 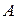 и
и 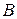 :
: 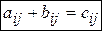 .
.
Дата добавления: 2015-12-22; просмотров: 674;
