Сетевые постановки транспортных задач
Пусть транспортная сеть состоит из  пунктов, соединенных направленными дугами (pi, pj),
пунктов, соединенных направленными дугами (pi, pj), 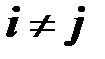 ,
,  . Пусть [0, T] – интервал оптимизации функционирования промышленно-транспортной системы (ПТС). Для каждого момента времени
. Пусть [0, T] – интервал оптимизации функционирования промышленно-транспортной системы (ПТС). Для каждого момента времени  на множестве P пунктов сети определена функция производства и потребления qi(t). Если
на множестве P пунктов сети определена функция производства и потребления qi(t). Если  , то пункт производства pi называется источником, если
, то пункт производства pi называется источником, если  , то пункт потребления pj называется стоком, и если
, то пункт потребления pj называется стоком, и если 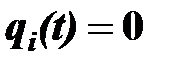 , то пункт pi называется перевалочным, t=0,1,…,T. Каждый путь (pi, pj) характеризуется пропускной способностью
, то пункт pi называется перевалочным, t=0,1,…,T. Каждый путь (pi, pj) характеризуется пропускной способностью 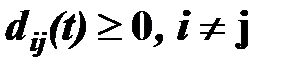 , и транспортным запаздыванием
, и транспортным запаздыванием 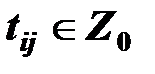 . При i=jdii(t) означает величину емкости склада пункта pi. Обозначим через Uij(t), t = 0,1,…,T объем поставок на пути (pi, pj), выходящий в момент t из пункта pi и приходящий в момент t + tij в пункт pj. Если путь (pi, pj) отсутствует или t + tij > T, то полагаем Uij(t) = 0. Ясно, что все Uij(Т) = 0,
. При i=jdii(t) означает величину емкости склада пункта pi. Обозначим через Uij(t), t = 0,1,…,T объем поставок на пути (pi, pj), выходящий в момент t из пункта pi и приходящий в момент t + tij в пункт pj. Если путь (pi, pj) отсутствует или t + tij > T, то полагаем Uij(t) = 0. Ясно, что все Uij(Т) = 0,  . Поставка Uii(t) означает запас пункта pi в момент t. Поэтому tii = 1. Пусть cij(t),
. Поставка Uii(t) означает запас пункта pi в момент t. Поэтому tii = 1. Пусть cij(t),  , расходы на перевозку единицы объема поставок из момента pi. Для каждого пункта потребления pj период, в течении которого отсутствуют поставки, равен [0, ti – 1], где ti = min(tji),
, расходы на перевозку единицы объема поставок из момента pi. Для каждого пункта потребления pj период, в течении которого отсутствуют поставки, равен [0, ti – 1], где ti = min(tji),  . Будем предполагать, что запаса в нулевой момент времени нет, т.е. справедливо
. Будем предполагать, что запаса в нулевой момент времени нет, т.е. справедливо
 .
.
Задача оптимизации функционирования промышленной транспортной системы ставится как задача минимизации суммарных транспортных расходов и расходов на хранение.
 .
.
Ограничения:
 ,
,
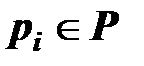 ,
,
 ,
,
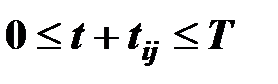 ,
,  ,
,
 .
.
Задачу будем называть динамической транспортной задачей (ДТЗЗ) в сетевой постановке. Очевиден содержательный смысл ограничений: уравнение является балансным соотношением; неравенство означает неотрицательность поставок, ограниченных пропускными способностями коммуникаций; время прибытия и время отправления поставок должны принадлежать интервалу оптимизации [0, T]; условия являются начальными и конечными условиями на запасы.
Учитывая ограничения и суммируя по t уравнение , получим для каждого пункта pj соотношение
 .
.
Суммированием по i соотношения получим уравнение
 ,
,
доставляющее необходимое условие разрешимости ДТЗЗ в сетевой постановке.
Дата добавления: 2015-12-22; просмотров: 1007;
