Динамическая транспортная задача с задержками
Пусть транспортная система связывает m пунктов производства Ai, i=1,…, m, и n пунктов потребления Bj, j=1,…,n. Предполагается, что каждый пункт производства Aj соединен коммуникациями со всеми пунктами потребления Bj. Для каждого момента времени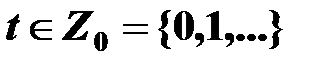 
обозначим:
ai(t) – объем производства;
xiA(t) – запас в пункте производства Ai;
Bj(t) – спрос;
xjB(t) – запас в пункте потребления Bj;
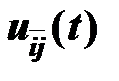- объем поставок, выходящий в момент t из Ai в Bj;
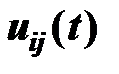- объем поставок, поступающий в момент t из Ai на Bj;
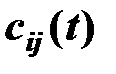- приведенные транспортные расходы;
, 
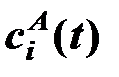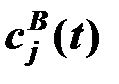- приведенные расходы на хранение соответственно в пунктах Ai и Bj.
Время движения из Ai в Bj обозначим tij и будем называть задержкой (транспортным запаздыванием); считаем, что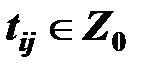 
для всех i=1,…,m, j=1,…,n. Если же в момент t движение между пунктами Ai и Bj закрыто, то перевозка 
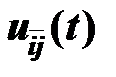не рассматривается.
Будем исследовать режим работы, в котором каждый пункт потребления Bj имеет возможность получать поставки из всех пунктов производства Ai, в моменты времени T0, T0+1,… T0+T-1. Интервал оптимизации всех пунктов потребления равен [T0, T0+T-1] и состоит из T тактов. В нашем случае каждый пункт производства должен иметь возможность сделать T поставок в каждый пункт потребления, и потому интервал времени работы поставщика Aj на потребителя Bj равен [T0-tij, T0-tij+T-1]. Объединяя все указанные интервалы, получим общий интервал функционирования поставщика
,
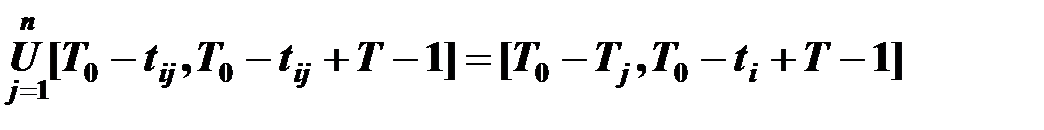где Ti = max(tij,…, tin), ti = min(ti1,…, tin)
Отметим, что периоды оптимизации поставщиков в общем случае различны и смещены во времени. Если все задержки tij одинаковы, то интервалы, оптимизации поставщиков равны и состоят (так же, как и для потребителей) из T тактов. Если же задержки tij=0, то интервалы оптимизации поставщиков и потребителей совпадают. Такой режим работы изучался, например, в /4, 5/.
Поставщик Ai может сделать поставку в момент T0-Ti+ti в пункт потребления Bj, если этот момент времени входит в интервал [T0-tij, T0-tij+T-1] обслуживания пунктом Ai пункта Bj. Другими словами, должно выполнятся неравенство: T0-Tj£T0-Ti+tj£T0-tij+T-1, или, что тоже самое: Ti-tij£ti£Ti-tij+T-1. Поставка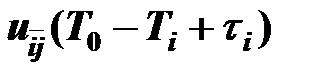 
, разрешенная в момент T0-Ti+ti , из Ai в Bj придет в момент времени T0+t=T0-Ti+ti+tij. Текущее время t потребителей связано с текущим временем ti поставщика Ai соотношением 
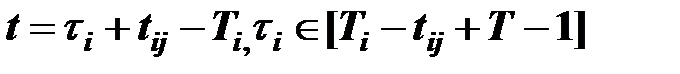, а объемы поставок 
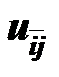и объемы получения 
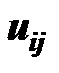- соотношением 
.
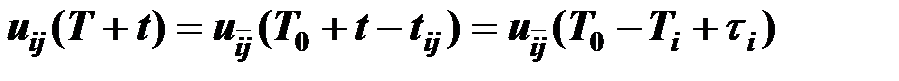Обозначим через Gi(T0-Ti+ti) множество индексов j пунктов потребления Bj, в которые пункт Ai в момент времени T0-Ti+ti может выполнить поставки, прибывающие в эти пункты не ранее момента времени T0 и не позднее T0+T-1. Для фиксированных i и ti индекс j принадлежит множеству Gi(T0-Tj+ti), если справедливо неравенство Ti£ti+tij£Tj+T-1, множества Gi(T0-Ti+ti) совпадают со множеством всех индексов j=1,…,n.
Общий интервал оптимизации системы поставщиков равен объединению всех интервалов оптимизации поставщиков
,
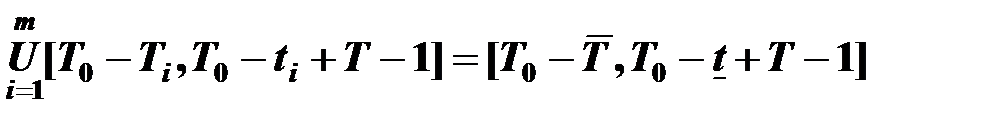где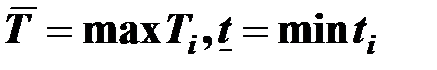 
.
Таким образом, предлагаемый режим работы приводит к функционированию системы потребителей Bj, j=1,…,n, в интервале [T0,T0+T-1], системы поставщиков – в интервале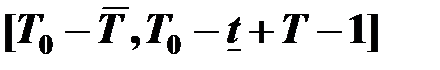 
и транспорта – в интервале 
.
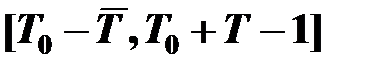Возможны и другие режимы работы. Например, система поставщиков имеет один и тот же интервал оптимизации [0, T-1], а интервалы оптимизации потребителей могут быть равными по продолжительности, но смещенными во времени и т.д.
В описываемом режиме функционирования и при заданных программах поставщиков и потребителей оптимизация перевозок рассматривается как задача минимизации функционала транспортных расходов и суммарных расходов на хранение
,
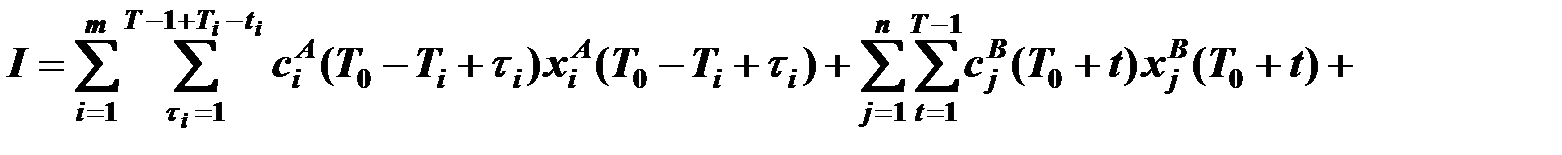
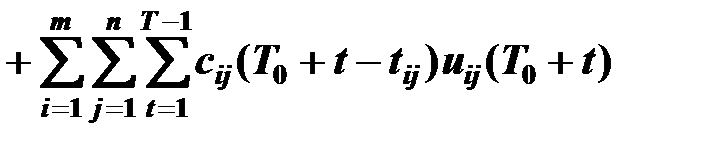при ограничениях, задаваемых:
а) уравнениями динамики запасов у поставщиков и потребителей
,
,
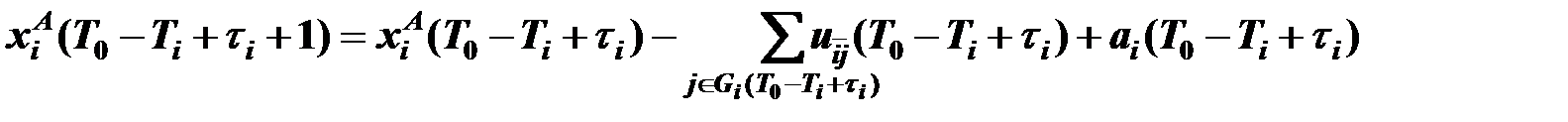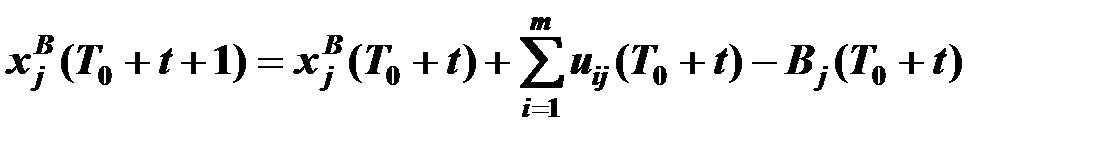б) уравнением связи поставщиков и потребителей
,
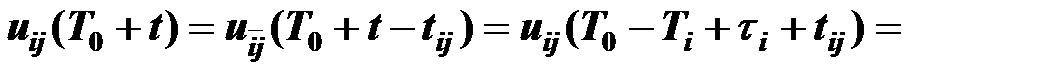
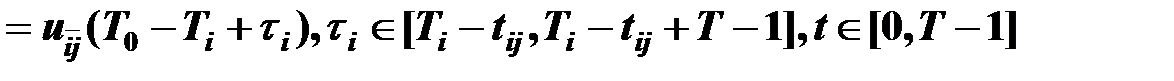в) начальными и конечными условиями
,
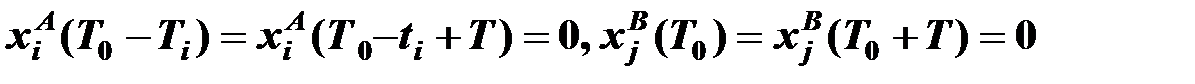г) условиями неотрицательных запасов и перевозок
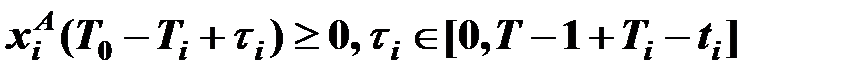, (15)
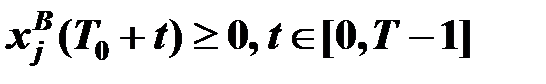, (16)
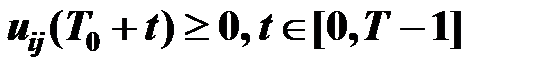. (17)
Если все транспортные задержки нулевые или совпадают, то постановка превращается в ДТЗ. Сформулированную задачу будем называть динамической транспортной задачей с задержками (ДТЗЗ).
Уравнение динамики изменения суммарного объема запасов
,
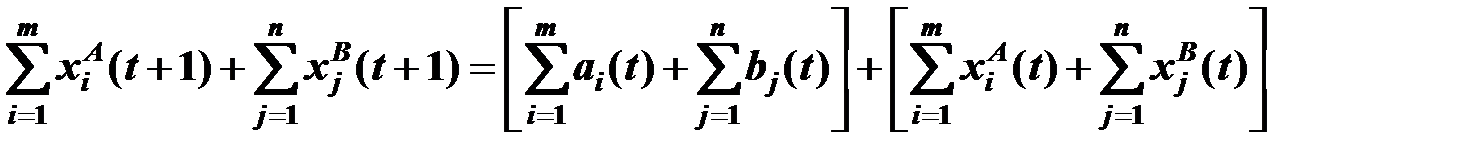используется для сведения ДТЗ к серии СТЗ. В /4/ ДТЗ характеризуется как общая задача линейного программирования, и для ее решения предлагается метод динамического линейного программирования, учитывающий специфику ДТЗ
Дата добавления: 2015-12-22; просмотров: 1637;