Задачи линейного программирования. Стандартная математическая формулировка общей задачи линейного программирования выглядит так: требуется найти экстремальное значение показателя эффективности

Стандартная математическая формулировка общей задачи линейного программирования выглядит так: требуется найти экстремальное значение показателя эффективности (целевой функции)

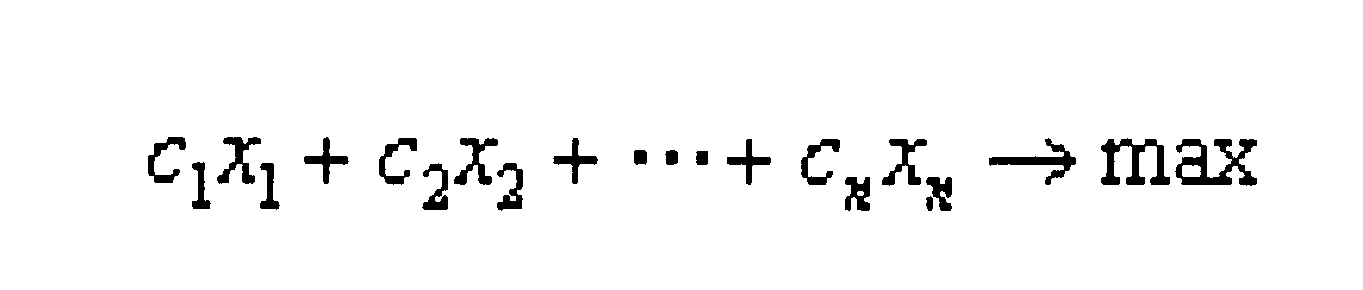
(линейной функции элементов решения 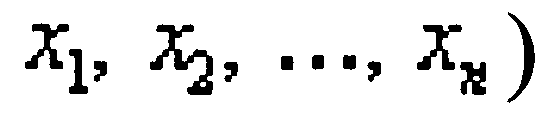накладываемых на элементы решения)

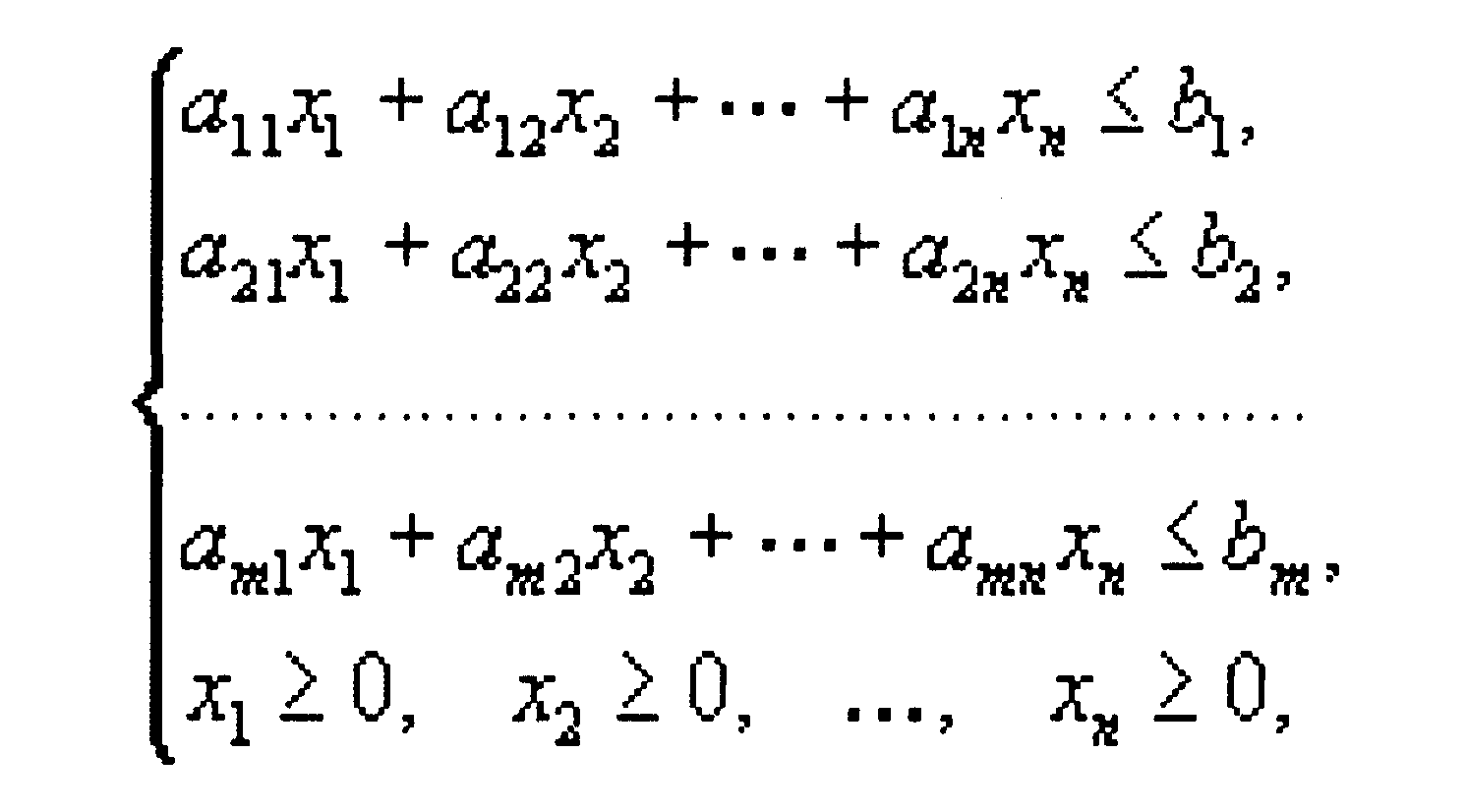
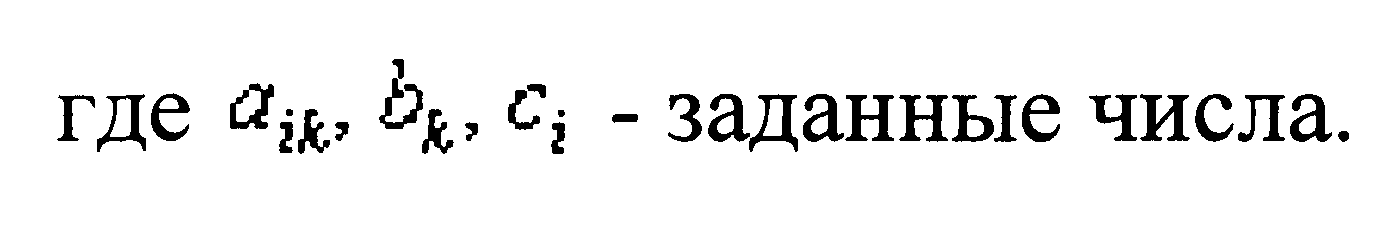
Что касается существующих методов решения этой задачи с числом переменных, больших двух, то в их основе лежат те же идеи, на которые опираются при разработке графического подхода. Конечно, в случае сильного увеличения числа переменных и ограничений техника получения решения заметно усложняется, но она опирается на совершенно стандартные, хорошо разработанные алгоритмы (возникающие трудности связаны лишь с ростом объема необходимых вычислений).

Общую постановку задачи линейного программирования можно записать в более компактной форме, если воспользоваться следующим правилом

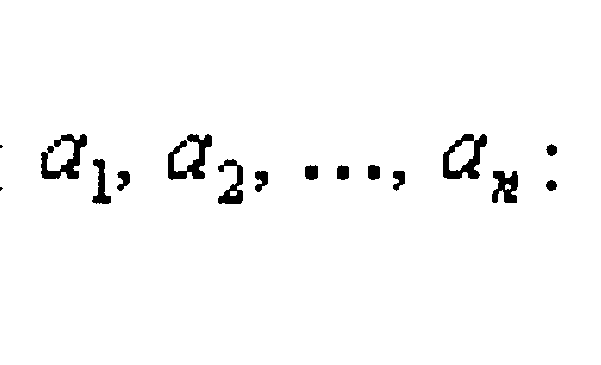
Правило сокращенного суммирования.

Для обозначения суммы чисел

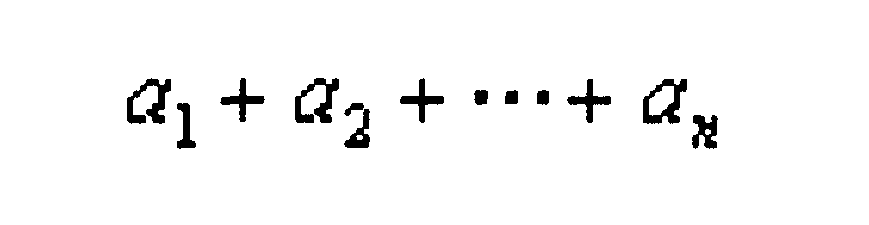
принята такая запись:

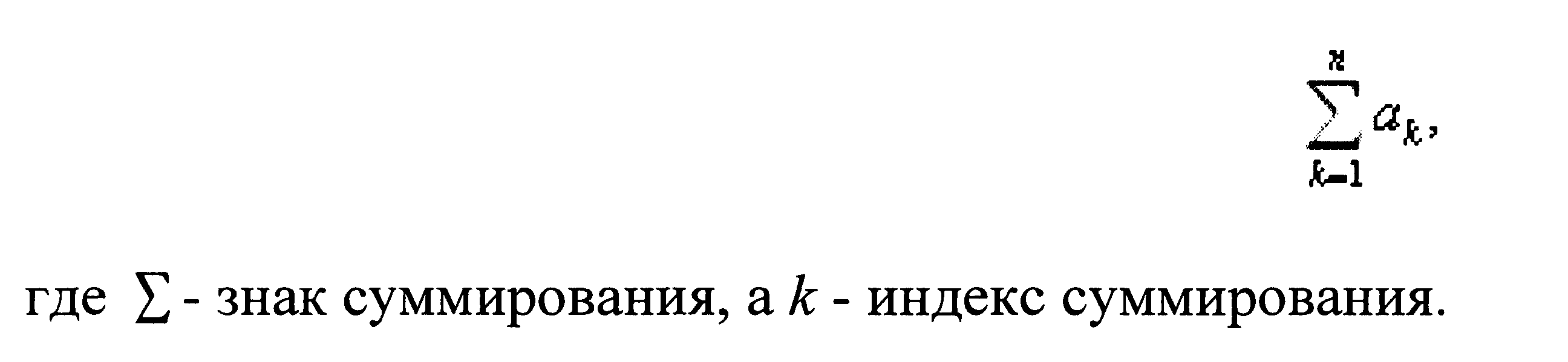
Это обозначение очень удобно:

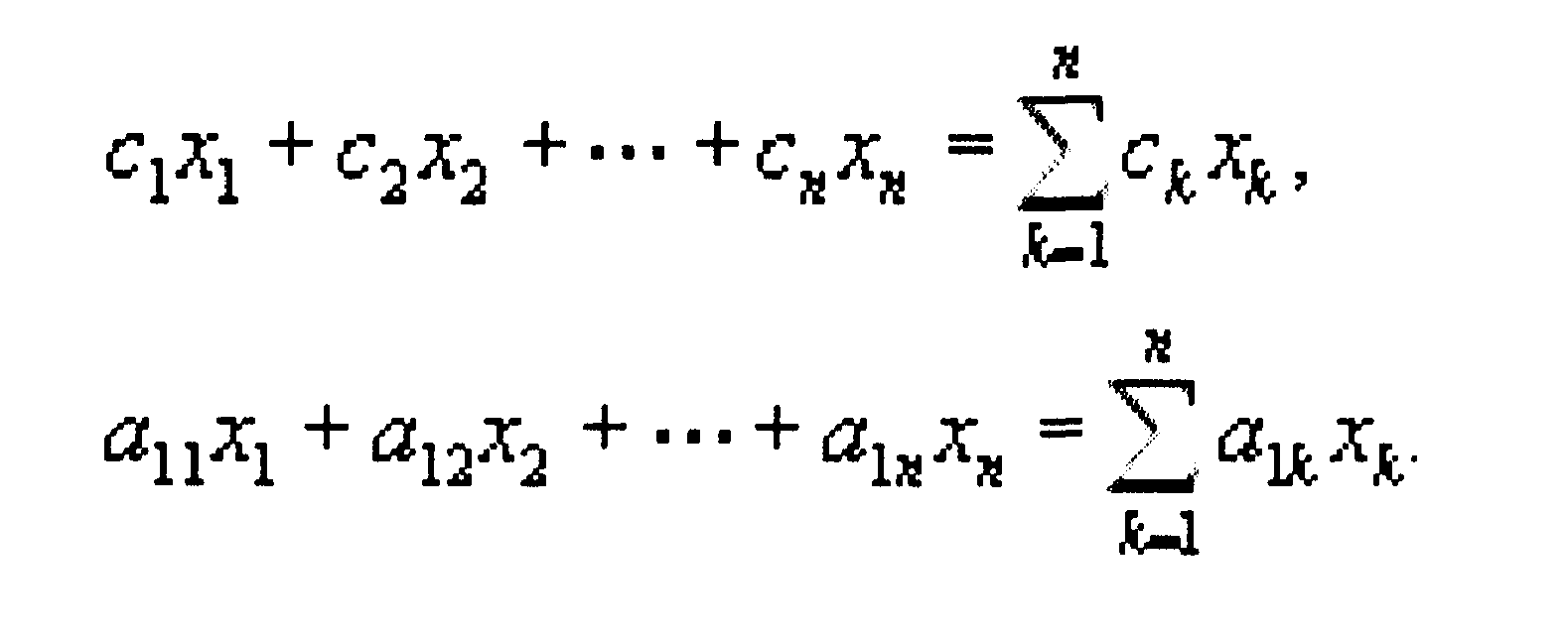
А вот как выглядит запись общей задачи линейного программирования:

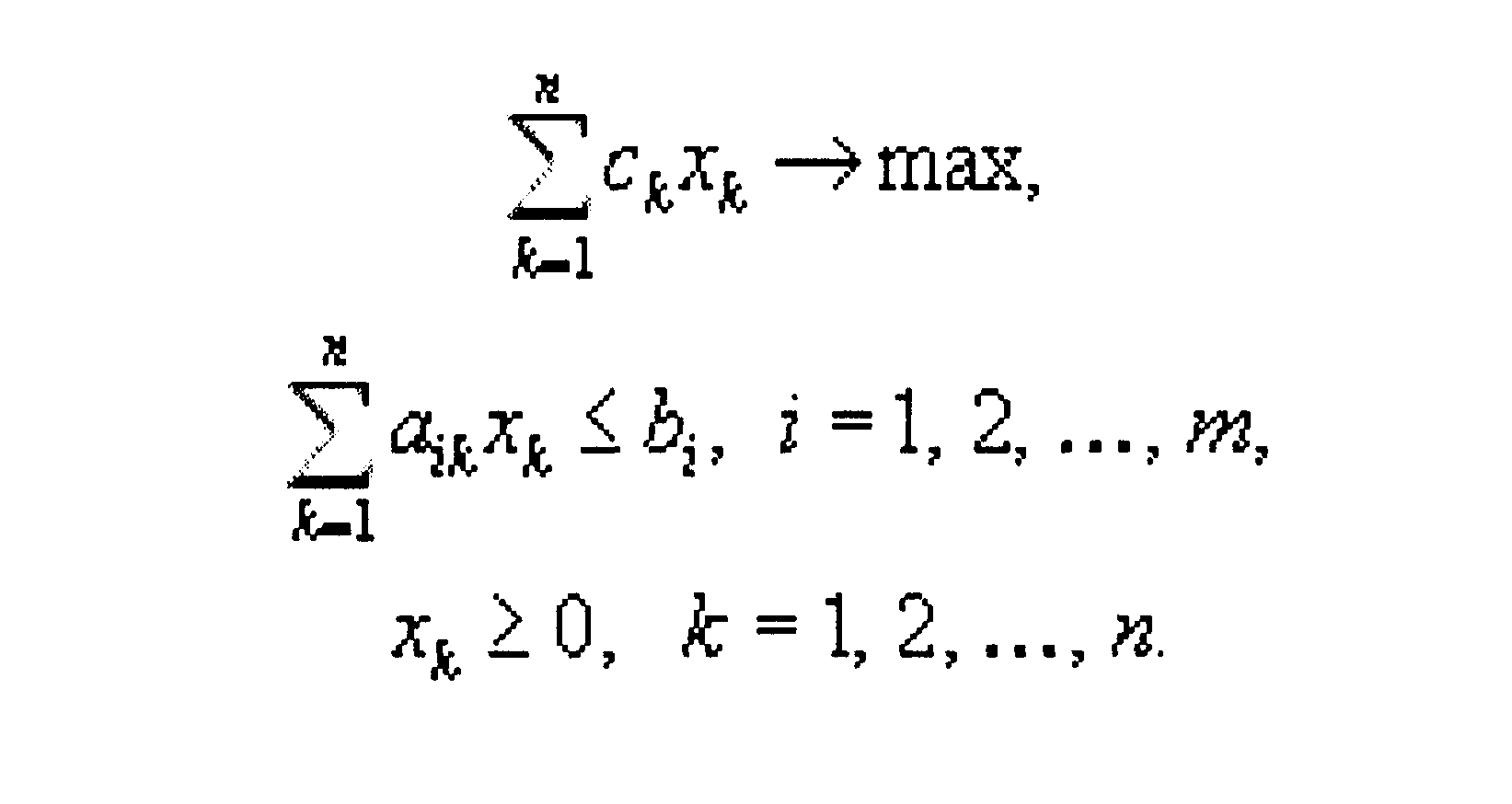
1.1. Однородная транспортная задача

Однородная транспортная задача есть прикладная задача линейного программирования, в которой требуется найти оптимальный план транспортировки некоторого однородного продукта из конечного числа пунктов поставки с заданными объемами производства в конечное число пунктов потребления с известными объемами потребностей:

• минимизирующий суммарную стоимость транспортировки,

• не превышающий объем производства в каждом пункте поставки,

• полностью покрывающий потребности в каждом пункте потребления,

при заданной стоимости перевозки единицы транспортируемого продукта между каждой парой пунктов поставки и потребления.

Транспортная задача была впервые сформулирована Хитчкоком и с тех пор применяется для решения практических задач доставки и распределения однородных продуктов. В наиболее наглядном виде постановку задачи отражает следующая формальная модель.

Имеется т пунктов поставки (поставщиков) и п пунктов потребления некого однородного продукта. Для каждого поставщика i =1…m задан объем производства 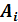, а для каждого потребителя j =1…n задан объем потребления 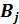и известна стоимость доставки единицы продукта 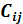из пункта производства iв пункт потребления j. Переменные 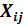характеризуют объем перевозки между каждым поставщиком i =1…mи потребителем j =1…n

В случае сбалансированного производства и потребления:

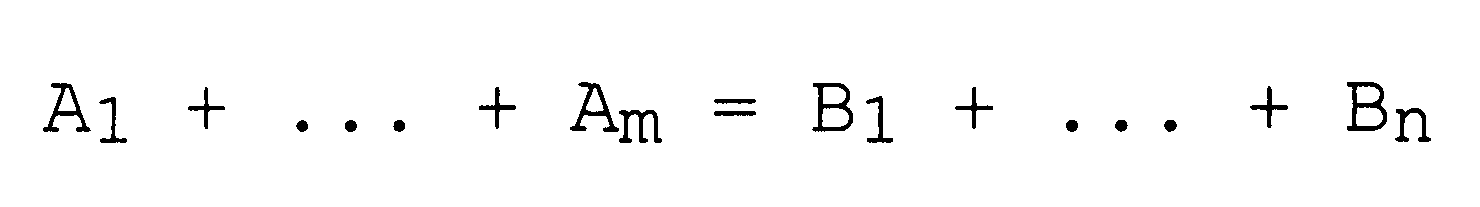
оптимальный план транспортировки соответствует минимизации линейной целевой функции:

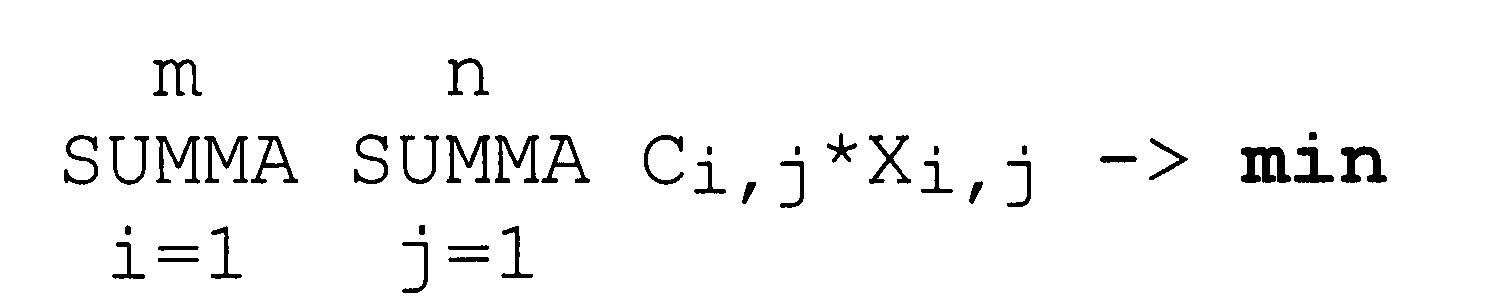
при т линейных ограничениях по поставке:

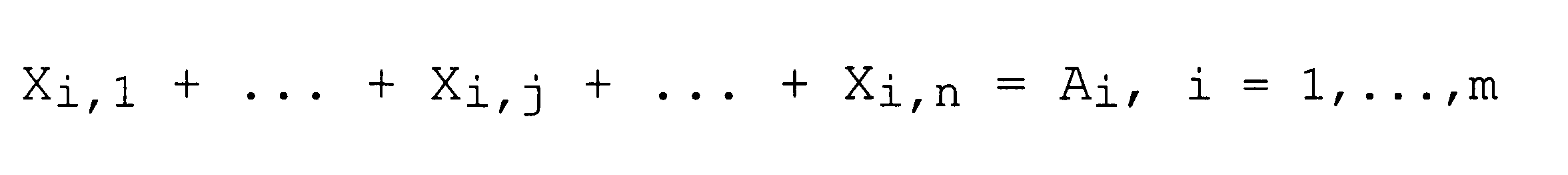
и п линейных ограничениях по потреблению:

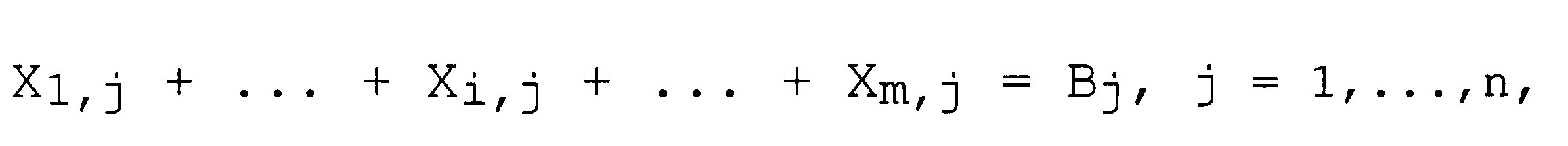
а также при очевидном условии неотрицательности управляемых переменных:

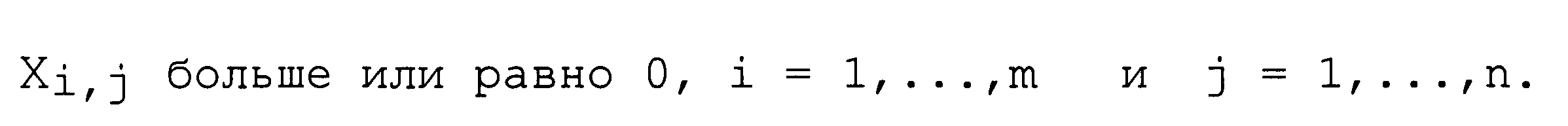
Из линейности критериальных и функциональных ограничений следует, что рассмотренная формальная модель транспортной задачи соответствует задаче линейного программирования. При целочисленных объемах производства и потребления транспортная задача гарантированно обладает целочисленным оптимальным планом. Это обстоятельство было впервые экспериментально подмечено Данцигом при применении симплекс-метода для решения данной задачи, что позволяет формально включить транспортную задачу в класс задач целочисленного линейного программирования, используя при этом для ее решения аппарат регулярного линейного программирования.